哈夫曼树及其算法实现

概念：

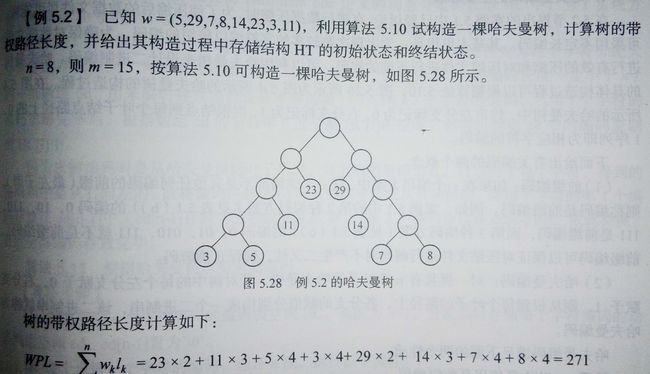
哈夫曼（Huffman）树又称最优二叉树或最优搜索树，是一种带权路径长度最短的二叉树。在许多应用中，常常赋给树中结点一个有某种意义的实数，称此实数为该结点的权。从树根结点到该结点之间的路径长度与该结点上权的乘积称为结点的带权路径长度(WPL)，树中所有叶子结点的带权路径长度之和称为该树的带权路径长度.
具体解释：http://lib.csdn.net/article/datastructure/13562

---

算法思想：

(1) 以权值分别为W1,W2．．．Ｗｎ的ｎ各结点，构成n棵二叉树T1,T2,．．．Tn并组成森林F={T1,T2,．．．Tn},其中每棵二叉树 Ti仅有一个权值为 Wi的根结点；

(2) 在F中选取两棵根结点权值最小的树作为左右子树构造一棵新二叉树，并且置新二叉树根结点权值为左右子树上根结点的权值之和（根结点的权值=左右孩子权值之和，叶结点的权值= Wi）

(3) 从F中删除这两棵二叉树，同时将新二叉树加入到F中;

(4) 重复(2)、(3)直到F中只含一棵二叉树为止，这棵二叉树就是Huffman树。

---

算法实现

这里我们使用数组来保存二叉树，由于哈夫曼树中没有度为1的节点，则一颗有n个叶子节点的哈夫曼共有2n-1个节点，可以保存在一个大小为2n-1的数组中。每个节点的结构表示为：

//哈夫曼树的存储表示
typedef struct
{
    int weight;    // 权值
    int parent, lChild, rChild;    // 双亲及左右孩子的下标 
}HTNode, *HuffmanTree;

哈夫曼树的节点保存在分配动态数组中，为了实现方便，数组的0号元素不使用，从1开始使用。叶子节点分布在前[1, n]，后面[n + 1, 2n - 1]（长度为n）存储非叶子节点。
（参考《数据结构（C语言版）（第二版）》（严蔚敏编）第138页）

---

C++代码

#include 
#include 
using namespace std;

//哈夫曼树的存储表示
typedef struct
{
    int weight;    // 权值
    int parent, lChild, rChild;    // 双亲及左右孩子的下标 
}HTNode, *HuffmanTree;


// 选择权值最小的两颗树 
void SelectMin(HuffmanTree hT, int n, int &s1, int &s2)
{
    s1 = s2 = 0;

    int i;
    for(i = 1; i < n; ++ i){
        if(0 == hT[i].parent){
            if(0 == s1){
                s1 = i;
            }
            else{
                s2 = i;
                break;
            }
        }
    }
    if(hT[s1].weight > hT[s2].weight){
        int t = s1;
        s1 = s2;
        s2 = t;
    }

    for(i += 1; i < n; ++ i){
        if(0 == hT[i].parent){
            if(hT[i].weight < hT[s1].weight){
                s2 = s1;
                s1 = i;
            }else if(hT[i].weight < hT[s2].weight){
                s2 = i;
            }
        }
    }
}

// 构造有n个权值（叶子节点）的哈夫曼树 
void CreateHufmanTree(HuffmanTree &hT)
{
    int n, m;
    cin >> n;
    m = 2*n - 1;

    hT = new HTNode[m + 1];    // 0号节点不使用 
    for(int i = 1; i <= m; ++ i){
        hT[i].parent = hT[i].lChild = hT[i].rChild = 0;
    }
    for(int i = 1; i <= n; ++ i){
        cin >> hT[i].weight;    // 输入权值 
    }
    hT[0].weight = m;    // 用0号节点保存节点数量 

    /****** 初始化完毕, 创建哈夫曼树 ******/
    for(int i = n + 1; i <= m; ++ i){
        int s1, s2;
        SelectMin(hT, i, s1, s2);

        hT[s1].parent = hT[s2].parent = i;
        hT[i].lChild = s1; hT[i].rChild = s2;    // 作为新节点的孩子 
        hT[i].weight = hT[s1].weight + hT[s2].weight;    // 新节点为左右孩子节点权值之和 
    }
}

int HuffmanTreeWPL_(HuffmanTree hT, int i, int deepth)
{
    if(hT[i].lChild == 0 && hT[i].rChild == 0){
        return hT[i].weight * deepth;
    }
    else{
        return HuffmanTreeWPL_(hT, hT[i].lChild, deepth + 1) + HuffmanTreeWPL_(hT, hT[i].rChild, deepth + 1);
    }
}

// 计算WPL（带权路径长度） 
int HuffmanTreeWPL(HuffmanTree hT)
{
    return HuffmanTreeWPL_(hT, hT[0].weight, 0);
}

// 输出哈夫曼树各节点的状态 
void Print(HuffmanTree hT)
{
    cout << "index weight parent lChild rChild" << endl;
    cout << left;    // 左对齐输出 
    for(int i = 1, m = hT[0].weight; i <= m; ++ i){
        cout << setw(5) << i << " ";
        cout << setw(6) << hT[i].weight << " ";
        cout << setw(6) << hT[i].parent << " ";
        cout << setw(6) << hT[i].lChild << " ";
        cout << setw(6) << hT[i].rChild << endl;
    }
}

// 销毁哈夫曼树 
void DestoryHuffmanTree(HuffmanTree &hT)
{
    delete[] hT;
    hT = NULL;
}

int main()
{
    HuffmanTree hT;
    CreateHufmanTree(hT);
    Print(hT); 
    cout << "WPL = " << HuffmanTreeWPL(hT) << endl;
    DestoryHuffmanTree(hT);
    return 0;
}

用书上的例子做验证：

运行结果：