2019独角兽企业重金招聘Python工程师标准>>>

作者：阿布?

未经本人允许禁止转载

ipython notebook git版本

目录章节地址： 自己动手写一个印钞机第一章自己动手写一个印钞机第二章自己动手写一个印钞机第三章自己动手写一个印钞机第四章自己动手写一个印钞机第五章自己动手写一个印钞机第六章自己动手写一个印钞机第七章

简书目录章节地址： 自己动手写一个印钞机第一章自己动手写一个印钞机第二章自己动手写一个印钞机第三章自己动手写一个印钞机第四章自己动手写一个印钞机第五章自己动手写一个印钞机第六章自己动手写一个印钞机第七章自己动手写一个印钞机附录章

股票量化专题地址，请关注，谢谢！

前言：

本文使用python来做stock量化分析，涉及数据挖掘分析与机器学习方面知识，stock知识涉及的不多，本文涉及的策略都只是考虑单边做多不涉及做空。

关于量化的定义我不想从之前某本看过的书或者网络找来一段写上，事实上写这整篇文章我都尽量避免自己从任何之前看过的东西找来定义或者解释，我尽量使用大白话来说明一切，但是由于stock量化本身是个太庞大，细节非常多，知识体系也非常复杂的系统，所以一定会有恨多地方我将说不清楚，可以联系我，一起探讨，回到量化定义我的理解：通过对数据进行各种变换，分析stock时间序列数据，找到相对赢的概率大的特征，抽取特征组成规则，使用这个规则指导交易，其实我想说的就是找到一个方法炒股然后只赚不赔，哈哈，我下面会一步一步讲解到底如何做出这样的一个印钞机（看到这个词我就高兴?）再次强调由于我无法解释所有细节，并且知识体系也确实需要很多，我不能保证你能全部看懂我下面再写一些什么，还是哪句话，我会留下微信，如有问题，可以联系我一起探讨（文章最后有微信号，如果能看到哪里再说吧）。

非均衡胜负收益带来的必然非均衡胜负比例，目标由因子的能力解决一部分，模式识别提升关键的一部分

非均衡胜负收益是什么意思？意思简单说就是每次赢的钱比每次输的钱多

为什么这是串行的第一步呢，因为在stock交易中，交易者永远是处于不利的地位的，不利的情况就是你需要交手续费，你可能会说那个没有多少钱，如果你随机的胡乱买卖stock，在你有足够多的本钱的情况下交易足够多的次数，最后的结果一定是符合正太分布的，但是如果你每次要多交你1%的手续费，情况就大不一样了，赌场要抽头，不抽头的赌场一定有老千, 要吃人的赌场又抽头又出老千。

下面用代码描述这几种情况

"""
    设置100个赌徒
"""
gamblers = 100

"""
    赌场：简单设定每个赌徒一共有1000000一共想在赌场玩10000000次，你要是没钱了也别想玩了
    win_rate:   输赢的概率
    win_once:   没次赢的钱数
    loss_once:  没次输的钱数
    commission: 手续费这里简单的设置了0.01 1%
"""
def casino(win_rate, win_once=1, loss_once=1, commission=0.01):
    my_money = 1000000
    play_cnt = 10000000
    commission = commission
    for _ in np.arange(0, play_cnt):
        w = np.random.binomial(1, win_rate)
        if w:
            my_money += win_once
        else:
            my_money -= loss_once
        my_money -= commission
        if my_money <= 0:
            break
    return my_money

"""
    使用numba预编译加速，否则很慢
"""
casino_nb = nb.jit(casino)

"""
    天堂赌场，没有抽头，没有老千?
    heaven_moneys 100个
    都去了之后玩回来之后的结果
"""
heaven_moneys = [casino_nb(0.5, commission=0) for _ in np.arange(0, gamblers)]

"""
    没有抽头，有老千?
"""
moneys_low = [casino_nb(0.4, commission=0) for _ in np.arange(0, gamblers)]

"""
    有抽头，没有老千?
"""
moneys_commission = [casino_nb(0.5, commission=0.01) for _ in np.arange(0, gamblers)]

"""
    有抽头，有老千?
"""
moneys_low_commission = [casino_nb(0.4, commission=0.01) for _ in np.arange(0, gamblers)]

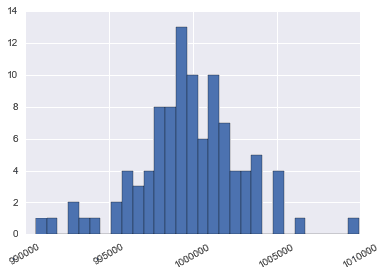
1. 天堂赌场，大家都能活下来，每个人亏的和赚的最后都不太多

plt.setp(plt.gca().get_xticklabels(), rotation=30)
pd.Series(heaven_moneys).hist(bins=30)

2. 有老千的赌场没有人能活下来，钱都归零了

pd.Series(moneys_low).hist()

3. 有抽头的赌场，看起来还不错，但是没有一个人赚钱的都是亏钱，当玩的次数再加大一个数量级，最后的结果也一定是归0

pd.Series(moneys_commission).hist()

help(casino)
    Help on function casino in module __main__:
    casino(win_rate, win_once=1, loss_once=1, commission=0.01)

假设我们的赌场没有老千，但是一定会有手续费，这样的话注意上面的赌场函数，我们不能期待我们有老千能力，也就是比如说你能有内部消息，把胜率提高到60%或者更高，如果你真的有，那么土豪我们做朋友吧?加微信一起发财, 那就只有每次赢钱和每次输钱的参数了

moneys = [casino_nb(0.5, commission=0.01, win_once=1.02, loss_once=0.98) for _ in np.arange(0, gamblers)]

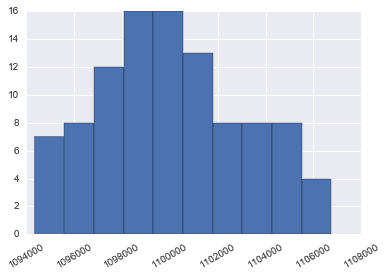
和上面那个直方图?对比你能发现每个人都能赢钱了，当我们设置了每次赢多出默认两个点，每次输少输两个点后

plt.setp(plt.gca().get_xticklabels(), rotation=30)
pd.Series(moneys).hist()

但是这样的话问题就来了，你凭什么能每次多赢，每次少输，其实很简单，每本关于stock的书籍都会提到止损的策略

这些策略的核心思想就是让赚钱stock的多赚钱，让亏损stock的少亏损(他们的文言文写的就是什么让利润奔跑✈️)这样的结果就是亏损的次数比赢钱的次数多，每次赢的钱比每次亏的钱多, 也就是高止盈位，低止损位

所以你发现了吗，不能平白无故的提高win_once, 对应的要降低win_rate，这是自己给自己摆千的节奏啊，所以win_rate可能是0.45甚至更低

moneys = [casino_nb(0.45, commission=0.01, win_once=1.02, loss_once=0.98) for _ in np.arange(0, gamblers)]
pd.Series(moneys).hist()

看到这个图了吧，最后的结果就是又回到了有输有赢的人，也就是产生了天堂赌场的感觉，这就是文章主题提到的。

非均衡胜负收益带来的必然非均衡胜负比例

上文提到了要实现 非均衡胜负收益, 怎么才能做到这个呢，试着把你的止盈位提高，降低你的止损位，比如说你10块钱买入一个stock，止盈15止损9块就附和目标，这样你能理解带来的必然非均衡胜负比例这个意思了吧。

但是这个止盈止损位合理吗，是不是应该调到14， 8呢或者20，9呢，这个就是量化系统所做的一般任务。

量化系统一般的组成形式

alpha在因子层下面，负责整个交易大框架的盈利，负责相对激进部分，一般包括最高止盈，最高止损，最大跌幅止损，最大回撤止损等等
因子作为组件插入alpha系统，因子可以是简单因子只发现信号，也可以有自己的止盈止损等等规则
beta系统作为风险控制层在alpha底层，更高权限的对交易进行风险控制，一般比较谨慎的做出干预，大盘风险，组合的合理相关性等等，因子是量化中很重要的概念，它的好坏可以说是整个系统能否真正盈利的关键，alpha好比有宏图大志的ceo它的目标要挣钱要挣好多好多钱，但是它可能只在上层社会中寻找睁钱的大方向，不会涉及细节，beta好比保守的cfo它的首要任务是不能让公司垮掉，要控制最大的系统风险，factor就是具体的一个个的销售了，它们的销售业绩直接就是整个公司的盈利或者亏损，自己有对产品的完整控制权，但alpha或者beta时不时的要管它们，对它们指手画脚，但是他们必须听从他两个，一般来说cfo的权限会大于ceo但也有设计成cfo，ceo等权限的

量化系统的一大部分功用就是维持这个非均衡胜负收益 , 非均衡胜负比例的交易系统能活下来，生存是第一需求，他们的目标就是生存

其实说的一点也不夸张，虽然alpha是激进的但它的激进只是为了与保守的beta一起能活下去，我们的系统要挣钱就要依靠因子的能力，因子的能力主要功用就是尽量平衡非均衡胜负收益与非均衡胜负比例需找最优点，活下来，并且能活得挺好。

因子有各种各样的方式去强化能力，需找最优，提高胜率，由于这篇文章的重点不是如何提高因子的能力，那个主题其实你也可以在其它一些量化分章中找到一些方法，下面只简单介绍一个实例，希望你能理解, 不理解也没关系，主题其实从下一章正式开始，那个才是印钞机的关键！

目标由因子的能力解决一部分

下面讲一个实例如何来提高因子的能力

黄金分割因子

本章使用黄金分割因子，简单说明一下它，黄金分割一种是视觉上的382，618，一种就是统计上的382，618 也就是mean和median的的区别如下代码所示：

def find_golden_point_ex(x_org, y_org, show=False):
    sp382 = stats.scoreatpercentile(y_org, 38.2)
    sp618 = stats.scoreatpercentile(y_org, 61.8)
    sp50 = stats.scoreatpercentile(y_org, 50.0)

    if show:
        x_org = np.array(x_org)
        sp382_list = [[x_org.min(), x_org.max()], [sp382, sp382]]
        sp618_list = [[x_org.min(), x_org.max()], [sp618, sp618]]
        sp50_list = [[x_org.min(), x_org.max()], [sp50, sp50]]

        TLineDrawer.plot_xy_with_other_x_y(x_org, y_org, '-', sp382_list, sp50_list, sp618_list)
    return sp382, sp50, sp618


def find_golden_point(x_org, y_org, show=False):
    cs_max = y_org.max()
    cs_min = y_org.min()

    sp382 = (cs_max - cs_min) * 0.382 + cs_min
    sp618 = (cs_max - cs_min) * 0.618 + cs_min
    sp50 = (cs_max - cs_min) * 0.5 + cs_min
    if show:
        x_org = np.array(x_org)
        sp382_list = [[x_org.min(), x_org.max()], [sp382, sp382]]
        sp618_list = [[x_org.min(), x_org.max()], [sp618, sp618]]
        sp50_list = [[x_org.min(), x_org.max()], [sp50, sp50]]

        TLineDrawer.plot_xy_with_other_x_y(x_org, y_org, '-', sp382_list, sp50_list, sp618_list)
    return sp382, sp50, sp618


def calc_golden(kl_pd, show=True, only_be=False):
    dk = True if kl_pd.columns.tolist().count('close') > 0 else False
    uq_close = kl_pd.close if dk else kl_pd.price

    if not hasattr(kl_pd, 'name'):
        kl_pd.name = 'unknown'

    g_382, g_500, g_618 = TLineAnalyse.find_golden_point(kl_pd.index, uq_close)
    if show and not only_be:
        plt.axes([0.025, 0.025, 0.95, 0.95])
        plt.plot(uq_close) if dk else plt.plot(uq_close.values)
        plt.axhline(g_618, color='c')
        plt.axhline(g_500, color='r')
        plt.axhline(g_382, color='g')
        _ = plt.setp(plt.gca().get_xticklabels(), rotation=30)
        plt.legend([kl_pd.name, 'g618', 'g500', 'g382'])
        plt.title('mean golden')
        plt.show()

    gex_382, gex_500, gex_618 = TLineAnalyse.find_golden_point_ex(kl_pd.index, uq_close)
    if show and not only_be:
        plt.axes([0.025, 0.025, 0.95, 0.95])
        plt.plot(uq_close) if dk else plt.plot(uq_close.values)
        plt.axhline(gex_618, color='c')
        plt.axhline(gex_500, color='r')
        plt.axhline(gex_382, color='g')
        _ = plt.setp(plt.gca().get_xticklabels(), rotation=30)
        plt.legend([kl_pd.name, 'gex618', 'gex500', 'gex382'])
        plt.title('median golden')
        plt.show()

    above618 = np.maximum(g_618, gex_618)
    below618 = np.minimum(g_618, gex_618)
    above382 = np.maximum(g_382, gex_382)
    below382 = np.minimum(g_382, gex_382)

    percents = [0.20, 0.25, 0.30, 0.70, 0.80, 0.90, 0.95]
    # precents = np.linspace(0.0, 1.0, 0.05)
    pts_dict = TLineAnalyse.find_percent_point(percents, uq_close)

    # import pdb
    # pdb.set_trace()
    below200 = np.minimum(*pts_dict[0.20])
    below250 = np.minimum(*pts_dict[0.25])
    below300 = np.minimum(*pts_dict[0.30])

    above700 = np.maximum(*pts_dict[0.70])
    above800 = np.maximum(*pts_dict[0.80])
    above900 = np.maximum(*pts_dict[0.90])
    above950 = np.maximum(*pts_dict[0.95])

    if show:
        plt.axes([0.025, 0.025, 0.95, 0.95])
        plt.plot(uq_close) if dk else plt.plot(uq_close.values)

        plt.axhline(above950, lw=3.5, color='c')
        plt.axhline(above900, lw=3.0, color='y')
        plt.axhline(above800, lw=2.5, color='k')
        plt.axhline(above700, lw=2.5, color='m')

        plt.axhline(above618, lw=2, color='r')
        plt.axhline(below618, lw=1.5, color='r')
        plt.fill_between(kl_pd.index, above618, below618,
                         alpha=0.1, color="r")

        '''
            *************I AM HERE*************
        '''
        plt.axhline(above382, lw=1.5, color='g')
        plt.axhline(below382, lw=2, color='g')
        plt.fill_between(kl_pd.index, above382, below382,
                         alpha=0.1, color="g")

        plt.axhline(below300, lw=2.5, color='k')
        plt.axhline(below250, lw=3.0, color='y')
        plt.axhline(below200, lw=3.5, color='c')

        _ = plt.setp(plt.gca().get_xticklabels(), rotation=30)
        plt.legend([kl_pd.name, 'above950', 'above900', 'above800', 'above700', 'above618', 'below618',
                    'above382', 'below382', 'below300', 'below250', 'below200'], bbox_to_anchor=(1.05, 1), loc=2,
                   borderaxespad=0.)
        plt.title('between golden')
        plt.show()

    return namedtuple('golden', ['g382', 'gex382', 'g500', 'gex500', 'g618',
                                 'gex618', 'above618', 'below618', 'above382', 'below382',
                                 'above950', 'above900', 'above800', 'above700', 'below300', 'below250', 'below200'])(
        g_382, gex_382,
        g_500, gex_500, g_618, gex_618, above618, below618, above382, below382,
        above950, above900, above800, above700, below300, below250, below200)

代码详情请自行查阅源代码：TLineGolden.py

import SymbolPd
import TLineGolden
# 选择一段符合买入条件的位置
kl_pd = SymbolPd.make_kfold_pd('usNOAH')[-82:-40]

如下图所示，这里选择了[-82:-40] 42天数据模拟，且这一天符合买入条件，这个条件你可以认为是

在blow382和above382之间
ma5 > ma10
大盘。。。
。。。。。。。。。。。。。。上面说的below和above就是因为有两种计算方式，如上代码所示一个是使用stats.scoreatpercentile，综合利用这两种计算方式，数值大的就是above小的就是below，上面1， 2，3，4可以是与的关系，也可以是更复杂的规则，更多请查询TLineGolden.py 或者参考附录

我就不叙述了，因子的规则有各种，变种也各异，没有必要赘述

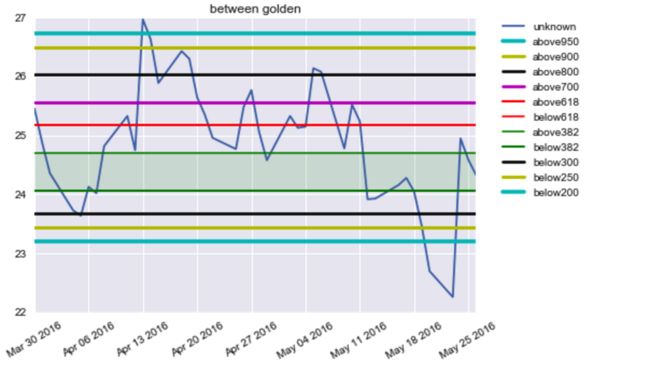
TLineGolden.calc_golden(kl_pd)

弹力止盈止损

如下mc_percent_default是默认的止盈止损位队列，mc_percent是经过最优计算出的我们会使用的止盈止损位队列，一会我们的主要任务就是演示怎么算出来的这个

# 各个止盈止损默认点，就如下图命中所示标准的200，250，300
mc_percent_default = [0.200, 0.250, 0.300, 0.382,
                0.618, 0.700, 0.800, 0.900, 0.950]


# 但我们不用上面那个默认的，为什么，因为那个的效果没下面这个好
mc_percent = [0.21828571428571428, 0.27285714285714285, 0.3274285714285714, 0.382,
              0.7271428571428571, 0.7817142857142857, 0.8362857142857143, 0.8908571428571428, 0.9454285714285714]

弹力止盈止损大概的做法就是如果股价下跌到below200我的最高止盈也随着下降一个档，如果股价上升一个档，最低止损也上升一个档位，直至向上或者向下击穿止最后一个盈止损位，这里简单用代码演示一下，只是演示！实际运行会复杂很多，因为有alpha，beta，因子本身及因子的父类等各种诱因，这里只单纯演示弹力止盈止损！

如下所示int_demo_trade 模拟初始24.16买入，通过买入价格初始化，初始化各个止盈止损价格，注意这里说的是价格，止盈止损位已经定义好了就是mc_percent，通过mc_percent和买入价确定了各个止盈止损价格，demo_trade模拟交易这里演示了弹力止盈止损是如何运作的。do_cnt_demo_trade封装一次交易

import WinLossAlloc
def int_demo_trade():
    # 假设以24.16买入，初始化，支撑阻力位
    bid_price = 24.16
    
    # 注意这里切分9个位，指定止损位是4个，那么止盈位就是5个了
    # 目的就是非均衡胜负与非均衡胜负比例的环境形成
    loss_cnt = 4
    golden = TLineGolden.calc_mc_golden(kl_pd, mc_percent, loss_cnt)
    
    wl = WinLossAlloc.init_golden_w_full(golden, bid_price)
    # 形成所以阻力有支撑，完整的弹力止盈止损位到齐
    print 'init supports : {}'.format(sorted(wl['supports'])), \
          'init resistances : {}'.format(sorted(wl['resistances']))
    print('\n')
    return wl

def demo_trade(wl):
    result_price = 0
    rs_cnt = 0
    while wl is not None:
        rs_cnt += 1
        supports = wl['supports']
        resistances = wl['resistances']
        # 45%概率win
        win = np.random.binomial(1, 0.45)
        if win:
            result_price = resistances[-1]
        else:
            result_price = supports[0]

        # 将输赢做为参数，重新计算出止盈止损位
        wl = WinLossAlloc.golden_map_wl_grid(win, wl)
        
        win_str = 'win' if win else 'loss'
        
        print(format('*', '*^108s'))
        print '{} result is {}'.format(rs_cnt, win_str)
        if wl:
            print 'supports : {}'.format(sorted(wl['supports'])), \
                  'resistances : {}'.format(sorted(wl['resistances']))
                  
    
    bid_price = 24.16
    print 'result profit is {}'.format((result_price - bid_price))
    print(format('©', '*^108s'))
    print('\n')
    
def do_cnt_demo_trade(t_cnt):
    while t_cnt > 0:
        wl = int_demo_trade()
        demo_trade(wl)
        t_cnt -= 1

# 模拟运行10次交易，通过输出是否看懂了什么是弹力止盈止损了呢
# 请尽量理解弹力止盈止损，不然继续向下不容易理解
do_cnt_demo_trade(10)
	# out
	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is win
	supports : [23.545157142857143, 23.802188571428573, 24.05922, 25.684842857142858] resistances : [25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	2 result is win
	supports : [24.05922, 25.684842857142858, 25.941874285714285] resistances : [26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	3 result is win
	supports : [25.941874285714285, 26.198905714285715] resistances : [26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	4 result is loss
	supports : [25.941874285714285] resistances : [26.198905714285715, 26.455937142857142]
	************************************************************************************************************
	5 result is win
	supports : [26.198905714285715] resistances : [26.455937142857142]
	************************************************************************************************************
	6 result is loss
	result profit is 2.03890571429
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is loss
	supports : [23.288125714285716, 23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	2 result is win
	supports : [23.545157142857143, 23.802188571428573, 24.05922] resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	3 result is loss
	supports : [23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858, 25.941874285714285]
	************************************************************************************************************
	4 result is loss
	supports : [23.545157142857143] resistances : [23.802188571428573, 24.05922]
	************************************************************************************************************
	5 result is win
	supports : [23.802188571428573] resistances : [24.05922]
	************************************************************************************************************
	6 result is loss
	result profit is -0.357811428571
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is loss
	supports : [23.288125714285716, 23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	2 result is win
	supports : [23.545157142857143, 23.802188571428573, 24.05922] resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	3 result is win
	supports : [24.05922, 25.684842857142858] resistances : [25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	4 result is win
	supports : [25.941874285714285] resistances : [26.198905714285715]
	************************************************************************************************************
	5 result is loss
	result profit is 1.78187428571
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is win
	supports : [23.545157142857143, 23.802188571428573, 24.05922, 25.684842857142858] resistances : [25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	2 result is win
	supports : [24.05922, 25.684842857142858, 25.941874285714285] resistances : [26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	3 result is win
	supports : [25.941874285714285, 26.198905714285715] resistances : [26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	4 result is loss
	supports : [25.941874285714285] resistances : [26.198905714285715, 26.455937142857142]
	************************************************************************************************************
	5 result is loss
	result profit is 1.78187428571
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is loss
	supports : [23.288125714285716, 23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	2 result is loss
	supports : [23.288125714285716, 23.545157142857143] resistances : [23.802188571428573, 24.05922, 25.684842857142858]
	************************************************************************************************************
	3 result is loss
	supports : [23.288125714285716] resistances : [23.545157142857143, 23.802188571428573]
	************************************************************************************************************
	4 result is loss
	result profit is -0.871874285714
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is win
	supports : [23.545157142857143, 23.802188571428573, 24.05922, 25.684842857142858] resistances : [25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	2 result is win
	supports : [24.05922, 25.684842857142858, 25.941874285714285] resistances : [26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	3 result is loss
	supports : [24.05922, 25.684842857142858] resistances : [25.941874285714285, 26.198905714285715, 26.455937142857142]
	************************************************************************************************************
	4 result is loss
	supports : [24.05922] resistances : [25.684842857142858, 25.941874285714285]
	************************************************************************************************************
	5 result is loss
	result profit is -0.10078
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is loss
	supports : [23.288125714285716, 23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	2 result is win
	supports : [23.545157142857143, 23.802188571428573, 24.05922] resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	3 result is win
	supports : [24.05922, 25.684842857142858] resistances : [25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	4 result is win
	supports : [25.941874285714285] resistances : [26.198905714285715]
	************************************************************************************************************
	5 result is win
	result profit is 2.03890571429
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is loss
	supports : [23.288125714285716, 23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	2 result is loss
	supports : [23.288125714285716, 23.545157142857143] resistances : [23.802188571428573, 24.05922, 25.684842857142858]
	************************************************************************************************************
	3 result is win
	supports : [23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858]
	************************************************************************************************************
	4 result is win
	supports : [24.05922] resistances : [25.684842857142858]
	************************************************************************************************************
	5 result is loss
	result profit is -0.10078
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is loss
	supports : [23.288125714285716, 23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	2 result is win
	supports : [23.545157142857143, 23.802188571428573, 24.05922] resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	3 result is loss
	supports : [23.545157142857143, 23.802188571428573] resistances : [24.05922, 25.684842857142858, 25.941874285714285]
	************************************************************************************************************
	4 result is win
	supports : [23.802188571428573, 24.05922] resistances : [25.684842857142858, 25.941874285714285]
	************************************************************************************************************
	5 result is loss
	supports : [23.802188571428573] resistances : [24.05922, 25.684842857142858]
	************************************************************************************************************
	6 result is loss
	result profit is -0.357811428571
	*****************************************************©*****************************************************


	init supports : [23.288125714285716, 23.545157142857143, 23.802188571428573, 24.05922] init resistances : [25.684842857142858, 25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	1 result is win
	supports : [23.545157142857143, 23.802188571428573, 24.05922, 25.684842857142858] resistances : [25.941874285714285, 26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	2 result is win
	supports : [24.05922, 25.684842857142858, 25.941874285714285] resistances : [26.198905714285715, 26.455937142857142, 26.712968571428569]
	************************************************************************************************************
	3 result is loss
	supports : [24.05922, 25.684842857142858] resistances : [25.941874285714285, 26.198905714285715, 26.455937142857142]
	************************************************************************************************************
	4 result is win
	supports : [25.684842857142858, 25.941874285714285] resistances : [26.198905714285715, 26.455937142857142]
	************************************************************************************************************
	5 result is loss
	supports : [25.684842857142858] resistances : [25.941874285714285, 26.198905714285715]
	************************************************************************************************************
	6 result is win
	supports : [25.941874285714285] resistances : [26.198905714285715]
	************************************************************************************************************
	7 result is loss
	result profit is 1.78187428571
	*****************************************************©*****************************************************

相信你看了代码和输出后就能理解弹力止盈止损了

本章内容本应分成两章从这里，否则内容太多，其它章内容没这么多，可先暂停，对不住

上面的实现是使用mc_percent = [0.21828571428571428, 0.27285714285714285, 0.3274285714285714, 0.382, 0.7271428571428571, 0.7817142857142857, 0.8362857142857143, 0.8908571428571428, 0.9454285714285714]我们说效果好，怎么定义效果好呢？答案就是运行了多次之后，结果最好，听起来是不是好傻，但是其实不管数学上名字叫的多吓唬人，公式看起来有多复杂，这种思想都是基础，蒙特卡洛就是这种的典型应用，凸优化其实也是，只不过它有计算梯度的方式，加快速度，但是这样你就很有可能陷入局部最优，一般就是先大概结出全局最优，然后带入求局部最优。

接下来我们用默认的就是mc_percent_default = [0.200, 0.250, 0.300, 0.382, 0.618, 0.700, 0.800, 0.900, 0.950]执行20000次，看看使用默认的值，多次之后输出的结果！

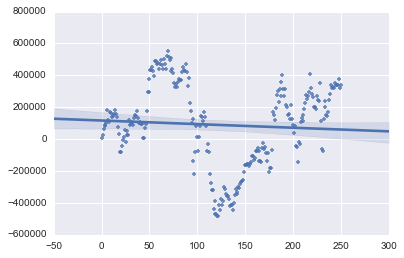
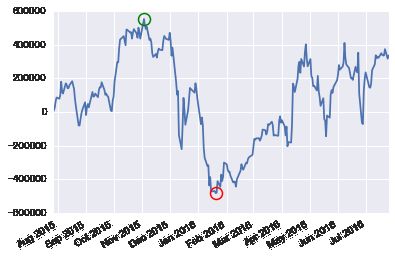
WinLossAlloc.show_golden_process(0.42, bp=24.3, pf_cnt=200, loop_cnt=20000)

执行弹力位止盈止损，0.42作为win_rate 第2图代表收益曲线，第3图代表在这些止盈止损位上的收益分布

上面的操作, 量化了mc_percent_default = [0.200, 0.250, 0.300, 0.382, 0.618, 0.700, 0.800, 0.900, 0.950]总公的收益是多少, 上升趋势是否平稳，收益分布是否合理，这样我们就有了一个评判mc_percent参数的量化准则了，下面开始寻找最优参数

使用蒙特卡洛方法分析最优

输赢比例
输赢资金的比例
最后总收益

很明显受益的关键是输赢资金的比例，所以思路最优输赢资金的比例

n_jobs=-1 使用并行加速

所有函数名称带nb的使用numba做编译加速处理，但效果一般，且使用numba会有一些限制条件

filter(lambda func: func.startswith('show_golden'), dir(WinLossAlloc)) ＃ out ['show_golden_mc_nb_process', 'show_golden_mc_nb_product_process', 'show_golden_mc_process', 'show_golden_mc_product_process', 'show_golden_nb_process', 'show_golden_process', 'show_golden_sco_process']

部分代码，详细代码请查询WinLossAlloc源代码

def show_golden_mc_product_process(w_rate, n_jobs=1, symbol=None, max_iter=8, bp=24.3, pf_cnt=200, loop_cnt=20000, p_outter_loop=1): """ 使用模特卡洛方式分析寻找最优参数, 排列最合所有元素 :param n_jobs: :param w_rate: :param symbol: :param max_iter: :param bp: :param pf_cnt: :param loop_cnt: :param p_outter_loop: :return: """

  """
      ⚠️控制max_iter, 15以上就会有上亿种排列组合了
  """
  loss_percents = np.linspace(0.0, 0.382, max_iter)
  win_percents = np.linspace(0.618, 1.0, max_iter)
  ls = list(itertools.combinations(loss_percents, g_mc_loss_cnt))
  ws = list(itertools.combinations(win_percents, g_mc_win_cnt))
  lws = list(itertools.product(ls, ws))

  # 暂时默认8核cpu,且把0及其它都归结为-1的范畴
  n_jobs = 8 if n_jobs <= 0 else n_jobs
  process_lws = []
  if n_jobs > 1:
      group_adjacent = lambda a, k: zip(*([iter(a)] * k))
      process_lws = group_adjacent(lws, n_jobs)
      # 将剩下的再放进去
      sf = -(len(lws) % n_jobs)
      if sf < 0:
          process_lws.append(lws[sf:])
  else:
      process_lws.append(lws)

  parallel = Parallel(
      n_jobs=n_jobs, verbose=0, pre_dispatch='2*n_jobs')

  out = parallel(
      delayed(_do_mc_product_process)(sub_lws, w_rate, symbol, bp, pf_cnt, loop_cnt,
                                      p_outter_loop)
      for sub_lws in process_lws)

  profits_dict = {}
  for sub_profits_dict in out:
      profits_dict.update(sub_profits_dict)

  return _golden_mc_process_profits(profits_dict)

def show_golden_mc_process(w_rate, symbol=None, max_iter=5000, bp=24.3, pf_cnt=200, loop_cnt=20000, p_outter_loop=1): """ 使用模特卡洛方式分析寻找最优参数 :param w_rate: :param symbol: :param max_iter: :param bp: :param pf_cnt: :param loop_cnt: :param p_outter_loop: :return: """ profits_dict = {} loss_percents = np.linspace(0.0, 0.382, 100) win_percents = np.linspace(0.618, 1.0, 100) golden_tuple = namedtuple('golden', ( 'below200', 'below250', 'below300', 'below382', 'above618', 'above700', 'above800', 'above900', 'above950'))

  if symbol is None:
      kl_pd = SymbolPd.make_kfold_pd('usNOAH')[-82:-40]
  else:
      kl_pd = SymbolPd.make_kfold_pd(symbol)

  for _ in np.arange(max_iter):
      loss_percent = np.random.choice(loss_percents, g_mc_loss_cnt, replace=False)
      win_percent = np.random.choice(win_percents, g_mc_win_cnt, replace=False)

      _golden_mc_process_cmp(kl_pd, loss_percent, win_percent, golden_tuple, profits_dict, w_rate,
                             bp, pf_cnt, p_outter_loop, loop_cnt, show=False)
  return _golden_mc_process_profits(profits_dict)

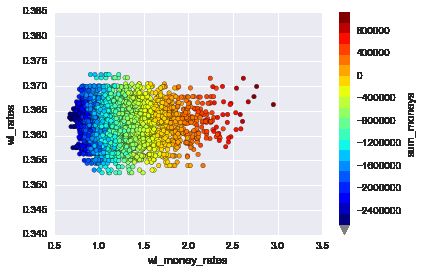
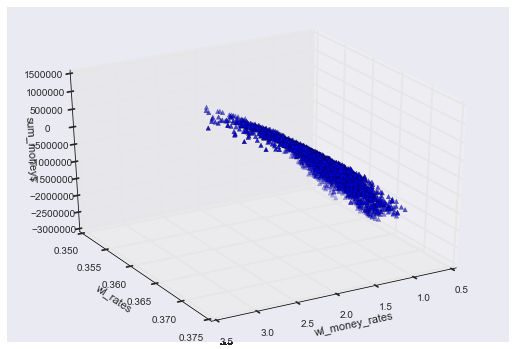
假设能达到0.42的胜率，这个0.42不代表最终能获胜的比例，只是每一次的胜率，可以认为这个值可以更高到0.5，最终的胜率由于高止盈位，低止损位会低于这个值，胜率其实在这个策略里是由各个止损止盈位决定的，这里是固定了这个参数，然后运用蒙特卡洛数学方法，这里是运用切片可能性然后排列最合所有元素, 首先可视化结果, 可以清楚的看出，要想最终能赢钱，关键点就是输赢钱的比例，每次赢的钱比输的钱越多，才有可能达到最后盈利（越向右红色的球越多，图例显示红球能够盈利）

%time wl_pd = WinLossAlloc.show_golden_mc_product_process(0.42, n_jobs=-1)
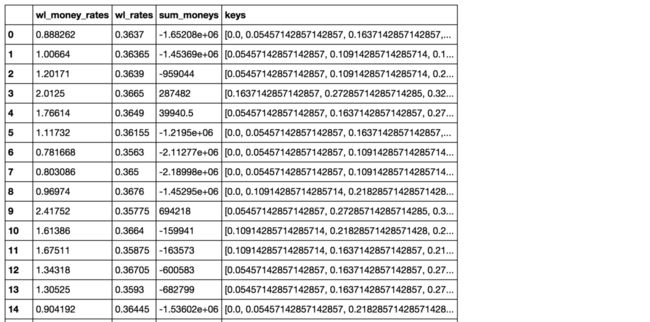
wl_pd
    # out
    CPU times: user 20.4 s, sys: 1.27 s, total: 21.7 s
    Wall time: 11min 44s

简单分析一下结果

wl_pd['sum_moneys'].mean(), wl_pd['wl_rates'].mean(), wl_pd['wl_money_rates'].mean()
    # out
    (-868311.44464704266, 0.36232785714285981, 1.2840789250773326)

pd.qcut(wl_pd['wl_money_rates'], 100).value_counts().head()
    # out
    (2.262, 2.952]    40
    (1.505, 1.516]    40
    (0.853, 0.868]    40
    (0.917, 0.928]    40
    (0.965, 0.975]    40
    Name: wl_money_rates, dtype: int64

pd.qcut(wl_pd['sum_moneys'], 10).value_counts()
    # out
	(-36011.0789, 1145831.81]        392
	(-312159.593, -36011.0789]       392
	(-519729.523, -312159.593]       392
	(-696741.476, -519729.523]       392
	(-869575.307, -696741.476]       392
	(-1034834.848, -869575.307]      392
	(-1211503.0155, -1034834.848]    392
	(-1416435.858, -1211503.0155]    392
	(-1706524.702, -1416435.858]     392
	[-2629618.186, -1706524.702]     392
	Name: sum_moneys, dtype: int64

还可以使用凸优化求解最优方程方法：详细代码请查询WinLossAlloc

        bnds = list((0, 0.382) for _ in range(g_mc_loss_cnt)) + list((0.618, 1) for _ in range(g_mc_win_cnt))
        opts = sco.minimize(min_func_st(how), guess_loss_precent + guess_win_precent, method='SLSQP',
                            bounds=bnds, options={'maxiter': max_iter})
                            
        问题是容易陷入局部最优，且不要太精度，可以先求全局最优在局部

opts, min_func = WinLossAlloc.show_golden_sco_process(0.42, how='sum_money')
ZLog.info(opts)
x_array = sorted(opts['x'])
ZLog.info(x_array)
min_func(x_array)
    # out
	     fun: 174767.91599998067
	     jac: array([ -3.12758046e+11,   1.14246519e+12,   4.51745309e+12,
	         1.48845611e+12,   6.39651998e+12,   3.96886976e+12,
	         3.69526407e+12,   6.19485965e+12,   7.27680427e+11,
	         0.00000000e+00])
	 message: 'Inequality constraints incompatible'
	    nfev: 11
	     nit: 1
	    njev: 1
	  status: 4
	 success: False
	       x: array([ 0.382     ,  0.32742857,  0.16371429,  0.05457143,  1.        ,
	        0.78171429,  0.89085714,  0.618     ,  0.94542857])
	[0.054571428571428569, 0.1637142857142857, 0.3274285714285714, 0.38200000000000001, 0.61799999999999999, 0.78171428571428569, 0.89085714285714279, 0.9454285714285714, 1.0]

下一步从mc 最优结果里筛选, 或者使用全局最优brust求解

从图分析，限制条件，找到n个解

filter_pd = wl_pd[(wl_pd['wl_money_rates'] > 2.5) & (wl_pd['wl_rates'] > 0.36)]
filter_pd

可视化人工从这n个里挑选最合适的 柱状要分布均匀，且达成非均衡这里选择第四个（992），阻力支撑保持非均衡，且200-500全分部，下降均匀这里不再一一描述，展现

WinLossAlloc.check_golden_mc_result(filter_pd, 0.42)

这里人工选择了第四个结果

[0.21828571428571428, 0.27285714285714285, 0.3274285714285714, 0.382, 0.7271428571428571, 0.7817142857142857, 0.8362857142857143, 0.8908571428571428, 0.9454285714285714]

发现这个值和最开始演示的弹力止盈止损中定义的mc_percent 是不是一模一样呢？mc_percent就是通过这个最优方式计算出来的

弹力止盈止损位, 参数的最优选择方法，这些就是本文演示的优化因子的能力的一部分，还有很多因子能力可以得到优化的地方，比如使用grid search选择合适的因子参数等等，这篇文章的重点不在因子能力的提升，如有问题私下沟通我，模式识别将是文章的重点

filter_pd.iloc[3], filter_pd.iloc[3]['keys']
    ＃ out
	(wl_money_rates                                              2.53375
	 wl_rates                                                     0.3612
	 sum_moneys                                                   710380
	 keys              [0.21828571428571428, 0.27285714285714285, 0.3...
	 Name: 1150, dtype: object,
	 '[0.21828571428571428, 0.27285714285714285, 0.3274285714285714, 0.382, 0.7271428571428571, 0.7817142857142857, 0.8362857142857143, 0.8908571428571428, 0.9454285714285714]')

因子的能力度量(选读与文章主题关系不大，下一章开始才能进入正题?)

非均衡胜负收益带来的必然非均衡胜负比例，目标由因子的能力解决一部分，模式识别提升关键的一部分看到这里很多技术细节不明白也不必特别在意，如果以后你能深入，都不是问题，现在能明白上面黑体部分的意思就差不多了

因子的能力的提升必须要有度量工具度量，不能仅仅凭一两方面就肯定或者否定什么，比如某个因子加alpha组合胜率达到90%，但你可能发现，这个因子在一年的回测周期中就生效了几次，那这个因子也不算是好因子，我的度量演示如下所示

使用黄金分割因子在一年回测周期中，对300只随机stock生效的度量结果

buy_factors = [{'XD': 42, 'class': BuyGoldenFactorClass, 'draw': True}]
sell_factors = []
parameters = {
                  'stop_loss_base_n': 4.0,
                  'stop_loss_base_n': 2.0,
                  'mv_close_atr': 3.5,
                  'mv_pre_atr': 2.0,
             }
cap, results, orders_pd, action_pd, all_fit_symbols = FactorUnitTest.random_unit_test(ret_cnt_need=300, 
    buy_factors=buy_factors, sell_factors=sell_factors, parameters=parameters, show=False)



rsc = metrics_rsc(*(cap, results, orders_pd, action_pd, all_fit_symbols))
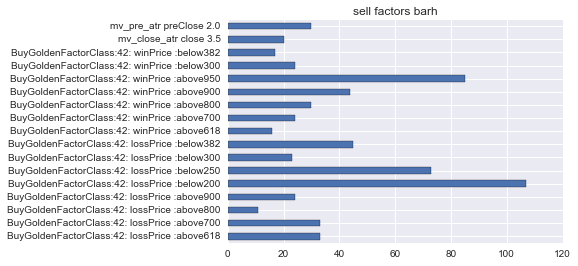
MetricsManger.make_metrics_from_rsc(rsc, METRICSTYPE.SYSMBOL_R_SCORES_GOLDEN.value)

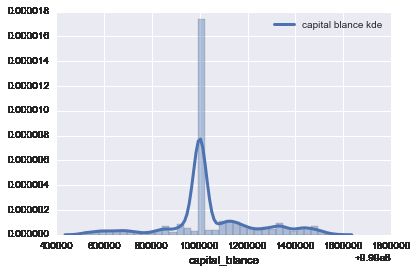
总资金变化情况

股本投入变化情况

因子生效频率

effect mean day: 1.7756097561

触发器分布情况

单子持有天数

keep days mean: 20.7683881064
keep days median: buy Date            2.016011e+07
buy Price           1.900000e+01
buy Cnt             8.141000e+03
Sell Price          1.981000e+01
MaxLoss                     -inf
key                 3.680000e+02
profit             -1.447280e+03
result             -1.000000e+00
R                  -0.000000e+00
sharpe              8.675231e-01
profit_cg          -8.085820e-03
profit_cg_hunder   -8.085820e-01
keep_days           1.600000e+01
dtype: float64

factor win effect = 0.0266040688576%
factor loss effect = 0.0704225352113%

每笔花费情况

cost info: 
moments_tuple(mean=160508.95918926984, std=48188.23197058294, skewness=-0.912289200610963, kurtosis=2.5446141847946633)

top win, top loss，最大回撤

更多度量相关请参考：git地址

铺垫讲到这一章就差不多了，我能力有限，不能通过这么短的篇幅和内容把所有事情讲清楚，如有不明白加我微信一起探讨，从下一章开始就是真正的‘印钞机’?之路了，直到这里为止，你只要知道大概能理解非均衡胜负收益带来的必然非均衡胜负比例，目标由因子的能力解决一部分就可以，至于具体的技术细节，暂时不用太在意，如果你能深入下去，这一切都不是事?

下一章地址自己动手写一个印钞机第二章

自己动手写一个印钞机第一章

作者：阿布?

未经本人允许禁止转载

前言：

本文使用python来做stock量化分析，涉及数据挖掘分析与机器学习方面知识，stock知识涉及的不多，本文涉及的策略都只是考虑单边做多不涉及做空。

非均衡胜负收益带来的必然非均衡胜负比例，目标由因子的能力解决一部分，模式识别提升关键的一部分

非均衡胜负收益是什么意思？意思简单说就是每次赢的钱比每次输的钱多

1. 天堂赌场，大家都能活下来，每个人亏的和赚的最后都不太多

2. 有老千的赌场没有人能活下来，钱都归零了

3. 有抽头的赌场，看起来还不错，但是没有一个人赚钱的都是亏钱，当玩的次数再加大一个数量级，最后的结果也一定是归0

但是这样的话问题就来了，你凭什么能每次多赢，每次少输，其实很简单，每本关于stock的书籍都会提到止损的策略

这些策略的核心思想就是让赚钱stock的多赚钱，让亏损stock的少亏损(他们的文言文写的就是什么让利润奔跑✈️)这样的结果就是亏损的次数比赢钱的次数多，每次赢的钱比每次亏的钱多, 也就是高止盈位，低止损位

所以你发现了吗，不能平白无故的提高win_once, 对应的要降低win_rate，这是自己给自己摆千的节奏啊，所以win_rate可能是0.45甚至更低

非均衡胜负收益带来的必然非均衡胜负比例

量化系统一般的组成形式

量化系统的一大部分功用就是维持这个非均衡胜负收益 , 非均衡胜负比例的交易系统能活下来，生存是第一需求，他们的目标就是生存

下面讲一个实例如何来提高因子的能力

黄金分割因子

弹力止盈止损

接下来我们用默认的就是mc_percent_default = [0.200, 0.250, 0.300, 0.382, 0.618, 0.700, 0.800, 0.900, 0.950]执行20000次，看看使用默认的值，多次之后输出的结果！

部分代码，详细代码请查询WinLossAlloc源代码

发现这个值和最开始演示的弹力止盈止损中定义的mc_percent 是不是一模一样呢？mc_percent就是通过这个最优方式计算出来的

因子的能力度量(选读与文章主题关系不大，下一章开始才能进入正题?)

使用黄金分割因子在一年回测周期中，对300只随机stock生效的度量结果

感谢?您能有耐心看到这里

如果有什么问题可以加阿布的微信

微信号：aaaabbbuu

你可能感兴趣的:(git,python,人工智能)

自己动手写一个印钞机 第一章

作者：阿布?

未经本人允许禁止转载

前言：

本文使用python来做stock量化分析，涉及数据挖掘分析与机器学习方面知识，stock知识涉及的不多，本文涉及的策略都只是考虑单边做多不涉及做空。

非均衡胜负收益带来的必然非均衡胜负比例，目标由因子的能力解决一部分，模式识别提升关键的一部分

非均衡胜负收益是什么意思？意思简单说就是每次赢的钱比每次输的钱多

1. 天堂赌场，大家都能活下来，每个人亏的和赚的最后都不太多

2. 有老千的赌场没有人能活下来，钱都归零了

3. 有抽头的赌场，看起来还不错，但是没有一个人赚钱的都是亏钱，当玩的次数再加大一个数量级，最后的结果也一定是归0

但是这样的话问题就来了，你凭什么能每次多赢，每次少输，其实很简单，每本关于stock的书籍都会提到止损的策略

这些策略的核心思想就是让赚钱stock的多赚钱，让亏损stock的少亏损(他们的文言文写的就是什么让利润奔跑✈️)这样的结果就是亏损的次数比赢钱的次数多，每次赢的钱比每次亏的钱多, 也就是高止盈位，低止损位

所以你发现了吗，不能平白无故的提高win_once, 对应的要降低win_rate，这是自己给自己摆千的节奏啊，所以win_rate可能是0.45甚至更低

非均衡胜负收益带来的必然非均衡胜负比例

量化系统一般的组成形式

量化系统的一大部分功用就是维持这个非均衡胜负收益 , 非均衡胜负比例的交易系统能活下来，生存是第一需求，他们的目标就是生存

下面讲一个实例如何来提高因子的能力

黄金分割因子

弹力止盈止损

接下来我们用默认的就是mc_percent_default = [0.200, 0.250, 0.300, 0.382, 0.618, 0.700, 0.800, 0.900, 0.950]执行20000次，看看使用默认的值，多次之后输出的结果！

部分代码，详细代码请查询WinLossAlloc源代码

发现这个值和最开始演示的弹力止盈止损中定义的mc_percent 是不是一模一样呢？mc_percent就是通过这个最优方式计算出来的

因子的能力度量(选读与文章主题关系不大，下一章开始才能进入正题?)

使用黄金分割因子在一年回测周期中，对300只随机stock生效的度量结果

感谢?您能有耐心看到这里

如果有什么问题可以加阿布的微信

微信号：aaaabbbuu

你可能感兴趣的:(git,python,人工智能)

自己动手写一个印钞机第一章