数据结构:栈的应用 C语言版 -(1)
一 进制转换:
十进制 N 和 其他进制 d 之间的转换 公式:
N = ( N ÷ d ) ∗ d + N % d N=(N\div d)*d+N\%d N=(N÷d)∗d+N%d
例: ( 1348 ) 10 = ( 2504 ) 8 (1348)_{10}=(2504)_8 (1348)10=(2504)8 运算过程如下:

示例:
#define _CRT_SECURE_NO_WARNINGS
#include 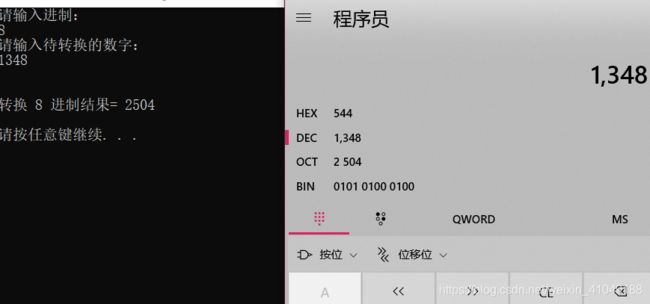

使用的栈结构见博客:数据结构:栈(Stack 链式存储结构) C语言版
2:基于中缀和后缀表达式的括号匹配和算式计算
基于栈的特性和就近匹配原则
中缀表达式:
符合我们习惯的数学表达式叫做中缀表达式 ,例如: 9 + ( 3 − 1 ) ∗ 5 + 8 / 2 9 + (3 - 1) * 5 + 8 / 2 9+(3−1)∗5+8/2 ,等这种日常表达式。
明显特正就是运算符号在数字中间
后缀表达式:
后缀表达式是一种不需要括号的后缀表达法,也称逆波兰表示。
例如:
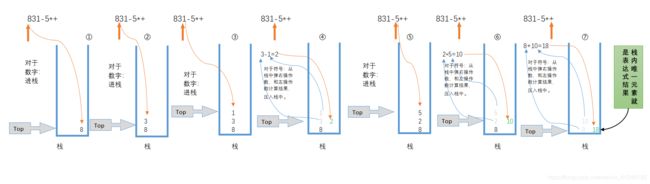
- ( 中 缀 ) 8 + ( 3 – 1 ) ∗ 5 = > ( 后 缀 ) 831 – 5 ∗ + (中缀)8 + ( 3 – 1 ) * 5 => (后缀)8 3 1 – 5 * + (中缀)8+(3–1)∗5=>(后缀)831–5∗+
- ( 中 缀 ) 1 + 2 ∗ 3 = > ( 后 缀 ) 123 ∗ + (中缀)1 + 2 * 3 => (后缀)1 2 3 * + (中缀)1+2∗3=>(后缀)123∗+
- ( 中 缀 ) 5 + 4 = > ( 后 缀 ) 54 + (中缀)5 + 4=>(后缀) 5 4 + (中缀)5+4=>(后缀)54+
明显特征就是运算符号在数字后面,后缀表达式更符合计算机运算习惯。
中缀转后缀
栈数据结构对于中缀转后缀规则:
遍历中缀表达式中的数字和符号
对于数字:直接输出
对于符号:
- 左括号:进栈
- 运算符号:与栈顶符号进行优先级比较,若栈顶符号优先级低:此符合进栈 (默认栈顶若是左括号,左括号优先级最低)若栈顶符号优先级不低:将栈顶符号弹出并输出,之后进栈。
- 右括号:将栈顶符号弹出并输出,直到匹配左括号(弹出左括号,不输出)
遍历结束:将栈中的所有符号弹出并输出。
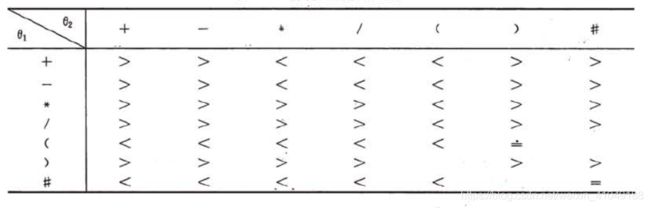
运算符的优先关系:
任意两个相继出现的算符 θ 1 \theta_1 θ1 和 θ 2 \theta_2 θ2 之间的优先关系之多是下面3中关系之一。
- θ 1 < θ 2 \theta_1 < \theta_2 θ1<θ2 , θ 1 \theta_1 θ1 的优先权低于 θ 2 \theta_2 θ2
- θ 1 = θ 2 \theta_1 = \theta_2 θ1=θ2 , θ 1 \theta_1 θ1 的优先权等于 θ 2 \theta_2 θ2
- θ 1 > θ 2 \theta_1 > \theta_2 θ1>θ2 , θ 1 \theta_1 θ1 的优先权高于 θ 2 \theta_2 θ2
示例:

基于栈的后缀表达式计算方法:
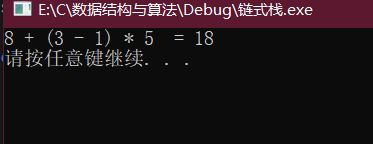
例: 8 + ( 3 − 1 ) ∗ 5 = = > 831 − 5 ∗ + 8+(3-1)*5==>831-5*+ 8+(3−1)∗5==>831−5∗+
算法实现
1:括号匹配
#define _CRT_SECURE_NO_WARNINGS
#include int main() { int a[4][4]; int (*p)[4]; p = a[0; return 0;} " ;
scanner(code);
system("pause");
return;
}
下面这段代码 a[0 少了一个 ] 号,进行测试括号匹配
#include #include "stdio.h"
#include "stdlib.h"
#include "string.h"
#include "linkstack.h"
int isNumber(char c)
{
return ('0' <= c) && (c <= '9');
}
int isOperator(char c)
{
return (c == '+') || (c == '-') || (c == '*') || (c == '/');
}
int isLeft(char c)
{
return (c == '(');
}
int isRight(char c)
{
return (c == ')');
}
int priority(char c)
{
int ret = 0;
if ((c == '+') || (c == '-'))
{
ret = 1;
}
if ((c == '*') || (c == '/'))
{
ret = 2;
}
return ret;
}
void output(char c)
{
if (c != '\0')
{
printf("%c", c);
}
}
void transform(const char* exp)
{
int i = 0;
LinkStack* stack = LinkStack_Create();
while (exp[i] != '\0')
{
if (isNumber(exp[i]))
{
output(exp[i]);
}
else if (isOperator(exp[i]))
{
while (priority(exp[i]) <= priority((char)(int)LinkStack_Top(stack)))
{
output((char)(int)LinkStack_Pop(stack));
}
LinkStack_Push(stack, (void*)(int)exp[i]);
}
else if (isLeft(exp[i]))
{
LinkStack_Push(stack, (void*)(int)exp[i]);
}
else if (isRight(exp[i]))
{
//char c = '\0';
while (!isLeft((char)(int)LinkStack_Top(stack)))
{
output((char)(int)LinkStack_Pop(stack));
}
LinkStack_Pop(stack);
}
else
{
printf("Invalid expression!");
break;
}
i++;
}
while ((LinkStack_Size(stack) > 0) && (exp[i] == '\0'))
{
output((char)(int)LinkStack_Pop(stack));
}
LinkStack_Destroy(stack);
}
int main()
{
transform("8+(3-1)*5");
printf("\n");
system("pause");
return 0;
}
#include "stdio.h"
#include "stdlib.h"
#include "linkstack.h"
int isNumber3(char c)
{
return ('0' <= c) && (c <= '9');
}
int isOperator3(char c)
{
return (c == '+') || (c == '-') || (c == '*') || (c == '/');
}
int value(char c)
{
return (c - '0');
}
int express(int left, int right, char op)
{
int ret = 0;
switch (op)
{
case '+':
ret = left + right;
break;
case '-':
ret = left - right;
break;
case '*':
ret = left * right;
break;
case '/':
ret = left / right;
break;
default:
break;
}
return ret;
}
int compute(const char* exp)
{
LinkStack* stack = LinkStack_Create();
int ret = 0;
int i = 0;
while (exp[i] != '\0')
{
if (isNumber3(exp[i]))
{
LinkStack_Push(stack, (void*)value(exp[i]));
}
else if (isOperator3(exp[i]))
{
int right = (int)LinkStack_Pop(stack);
int left = (int)LinkStack_Pop(stack);
int result = express(left, right, exp[i]);
LinkStack_Push(stack, (void*)result);
}
else
{
printf("Invalid expression!");
break;
}
i++;
}
if ((LinkStack_Size(stack) == 1) && (exp[i] == '\0'))
{
ret = (int)LinkStack_Pop(stack);
}
else
{
printf("Invalid expression!");
}
LinkStack_Destroy(stack);
return ret;
}
int main()
{
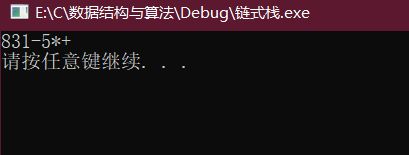
printf("8 + (3 - 1) * 5 = %d\n", compute("831-5*+"));
system("pause");
return 0;
}