实验（四）DPCM编码的实现和分析

DPCM编码原理简介

DPCM全称差分脉冲编码调制（Differential Pulse Code Modulation），是一种利用相邻像素的相关性去除空间冗余信息达到压缩目的的算法。

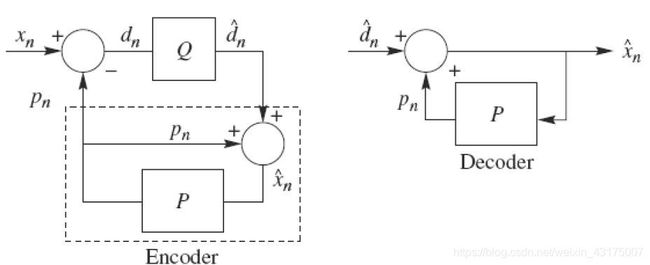
其中xn为输入信号，Q为量化器，dn=pn+xn为预测误差，P为延时器。

本实验采用前向预测，即每个像素左边的像素，大致算法如下：

以8bit图像为例，收到的灰度取值为[0，255]，与前一个像素作差和得到误差范围为[-255,255]。

需要将其范围转变为计算机可以表示的范围，先转变为单极性，即加上255，范围变为[0,510]。

8bit量化时，对其除以2^{（9-1）=2，510/2=255<2}8。

同理，4bit量化时，除以2^{（9-4）=32，510/32=15.94<2}4。

2bit量化时，除以2^{（9-2）=128，510\128=3.99<2}2。

重建图像时，即将预测值和误差值相加即可（编程时要注意误差计算时取值范围的变化）。

DPCM编码实验结果

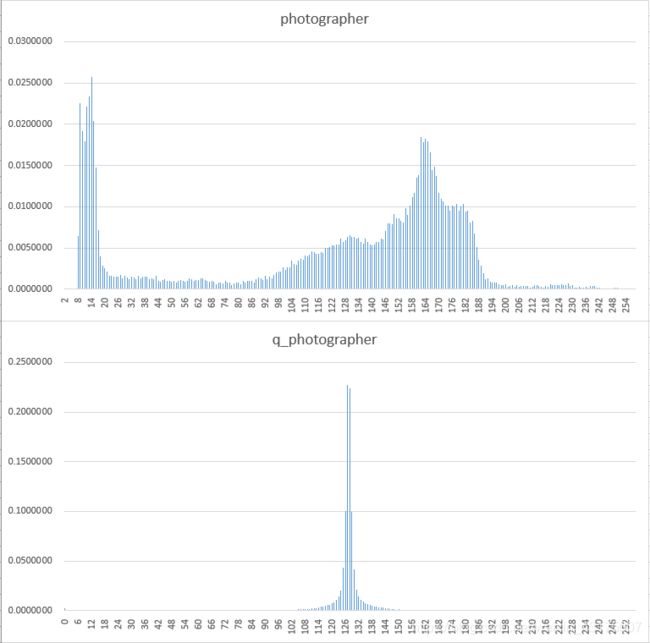
对256*256的8bit灰度yuv（4:2:0)图像进行DPCM量化编码，并对原题和误差图像进行概率分布统计。
实验代码和结果如下：
其中针对第一列的误差值设为128.

#include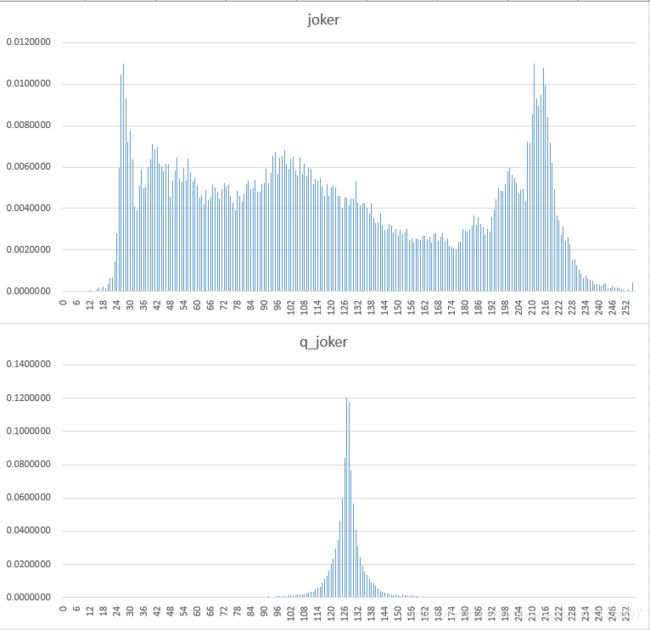
#include
#include
#include
#include
#include
using namespace std;
void dpcm(unsigned char *yBuf, unsigned char *qBuf, unsigned char *reBuf, int w, int h, int depth)
{
     	
	int r = pow(2, (double)(9 - depth));
	for (int i = 0; i < h; i++)
		for(int j = 0; j < w; j++)
		{
     
			if (j == 0)//第一列
			{
     
				qBuf[i * w] = ((yBuf[i * w] - 128) + 255) / pow(2, (double)(9 - depth)) ;
				reBuf[i * w] = qBuf[i * w] * pow(2, (double)(9 - depth)) + 255 - 128;
			}
			else
			{
     
				qBuf[i * w + j] = ((yBuf[i * w + j] - reBuf[i * w + j - 1]) + 255) / pow(2, (double)(9 - depth));
				reBuf[i * w + j] = qBuf[i * w + j] * pow(2, (double)(9 - depth)) - 255 + reBuf[i * w + j - 1];
			}
			if (qBuf[i * w + j] > 255)
				qBuf[i * w + j] = 255;
			if (qBuf[i * w + j] < 0)
				qBuf[i * w + j] = 0;
			if (reBuf[i * w + j] > 255)
				reBuf[i * w + j] = 255;
			if (reBuf[i * w + j] < 0)
				reBuf[i * w + j] = 0;
		}
}


int main(void)
{
     
	int bits_depth = 2;
	unsigned char *yBuf, *uBuf, *vBuf;
	int w = 256, h = 256;
	yBuf =  (unsigned char*)malloc(sizeof(unsigned char) * (w * h));
	uBuf =  (unsigned char*)malloc(sizeof(unsigned char) * (w * h / 4));
	vBuf =  (unsigned char*)malloc(sizeof(unsigned char) * (w * h / 4));
	FILE* src = NULL;
	src = fopen("E:\\大三下\\数据压缩\\实验四\\Lena.yuv","rb");
	if (src == NULL)
	{
     
		printf("error opening source file!\n");
		system("pause");
		exit(-1);
	}
	fread(yBuf, sizeof(unsigned char), w * h, src);
	fread(uBuf, sizeof(unsigned char), w * h / 4, src);
	fread(vBuf, sizeof(unsigned char), w * h / 4, src);
	fclose(src);
	unsigned char *qBuf, *reBuf;
	qBuf =  (unsigned char*)malloc(sizeof(unsigned char) * (w * h));
	reBuf =  (unsigned char*)malloc(sizeof(unsigned char) * (w * h));


	dpcm(yBuf, qBuf, reBuf, w,  h, bits_depth);


	FILE* obj1 = NULL;
	FILE* obj2 = NULL;
	obj1 = fopen("E:\\大三下\\数据压缩\\实验四\\q_Lena(2bit).yuv","wb");
	obj2 = fopen("E:\\大三下\\数据压缩\\实验四\\re_Lena(2bit).yuv","wb");
	if (obj1 == NULL || obj2 == NULL)
	{
     
		printf("error opening objective file!\n");
		system("pause");
		exit(-1);
	}
	fwrite(qBuf, sizeof(unsigned char), w * h, obj1);
	fwrite(uBuf, sizeof(unsigned char), w * h / 4, obj1);
	fwrite(vBuf, sizeof(unsigned char), w * h / 4, obj1);
	fwrite(reBuf, sizeof(unsigned char), w * h, obj2);
	fwrite(uBuf, sizeof(unsigned char), w * h / 4, obj2);
	fwrite(vBuf, sizeof(unsigned char), w * h / 4, obj2);
	fclose(obj1);
	fclose(obj2);


	//计算分布概率
	double fre_q[256] = {
     0};
	double fre_org[256] = {
     0};
	for (int i = 0; i < 256; i++)
	{
     
	    int count_q = 0, count_org = 0;
		for (int j = 0; j < w * h; j++)
		{
     
			if ((int)qBuf[j] == i)
				count_q ++;
			if ((int)yBuf[j] == i)
				count_org ++;
		}
		fre_q[i] = (double)count_q / w / h;
		fre_org[i] = (double)count_org / w / h;
	}
	char s[] = "symbol\tfrequency\n";
	FILE* data_q = fopen("E:\\大三下\\数据压缩\\实验四\\q_Lena(2bit).txt","w");
	FILE* data_org = fopen("E:\\大三下\\数据压缩\\实验四\\org_Lena.txt","w");
	if (data_q == NULL || data_org == NULL)
	{
     
		printf("error opening txt file!\n");
		system("pause");
		exit(-1);
	}
	fprintf(data_org, s);	
	fprintf(data_q, s);
	for (int i = 0;i < 256; i++)
	{
     
		fprintf(data_q,"%d\t%f\n",i, fre_q[i]);
		fprintf(data_org,"%d\t%f\n",i, fre_org[i]);
	}
	fclose(data_q);
	fclose(data_org);

其他图象略。
可以看出，8bit量化可以较好的重建图像。误差图像的灰度大多集中再128附近。因为误差0归一化为128.

评价重建图像：PSNR

PSNR，即Peak Signal to Noise Ratio，峰值信噪比，是一种评价图像的客观标准。其数学公式为：
$$PSNR=10\ast \lg (\frac{MA{X}^2}{MSE}）$$

其中：MAX指最大值，在8bit灰度图中即等于255.

MSE指均方误差Mean Square Error
$$MSE=\frac{{\sum }_{i=0}^M{\sum }_{j=0}^N(f(i,j)-f^{\prime }(i,j){)}^2}{MN}$$
具体到本实验中，f(x,y)和f’(x,y)即原图像和重建图像，MN即为图像的宽和高。

一般来说，PSNR值在20-40，越大还原质量越好。PSNR只是客观指标，与人眼主观特性有差别。

通过不同bit量化（8，4，2）的重建图像和PSNR如下：

要实现PSNR功能，可添加如下代码：

//计算PSNR
	int max = 255;
	double mse = 0;
	for (int i = 0; i < h; i++)
		for (int j = 0; j < w; j++)
		{
     
			mse += (yBuf[i * w + j] - reBuf[i * w + j]) * (yBuf[i * w + j] - reBuf[i * w + j]);
		}
	mse = (double)mse / (double)(w * h);
	double psnr = 10 * log10((double)(max * max) / mse);
	cout << "PSNR = " << psnr;
	system("pause");

所得实验结果如下，以Lena和photographer为例：

量化比特数	8	4	2	1
Lena.yuv	51.1227	14.8482	7.66344	7.60348
photographer.yuv	27.0756	9.91553	7.19489	7.05763

可以看出，8bit量化可以较好地还原原始8bit图像，但4bit量化开始就损失了很多信息，图像出现明显失真，已经无法成功较好地重建图像。PSNR也说明图像质量很低，比特数越低越明显。

编码效率

本实验比较了两种系统的编码效率：

1. 仅使用了熵编码
2. DPCM后进行熵编码

本实验熵编码使用地是Huffman编码，工具为老师提供的可执行文件huffcode.exe，具体cmd输入参数为：

huffcode -i test.yuv -o test.huff -c>test.txt

对量化误差图像进行压缩。

最后通过压缩比比较两者效率，结果如下：

图像名称	压缩前（yuv）(kB)	压缩后（huff）(kB)	压缩比（%）
Lena(without DPCM)	96	72.2	75.2
Lena(8bit)	96	46.1	48.02
Lena(4bit)	96	25	26.04
Lena(2bit)	96	23.3	24.27
photographer(without DPCM)	96	72.1	75.1
photographer(8bit)	96	41.7	43.44
photographer(4bit)	96	28.8	30.0
photographer(2bit)	96	25.7	26.77

可以看出，经过DPCM后再熵编码的压缩质量明显高于不进行DPCM的图像。

此外，为了维持图像质量，还得使用8bit量化的DPCM量化编码，不能贸然使用更低位数的DPCM，可能会导致重要图像信息的丢失。