特征工程——特征选择（Feature Selection）

特征选择是特征工程里的一个重要问题，其目标是寻找最优特征子集。特征选择能剔除不相关(irrelevant)或冗余(redundant )的特征，从而达到减少特征个数，提高模型精确度，减少运行时间的目的。另一方面，选取出真正相关的特征简化模型，协助理解数据产生的过程。

基本流程

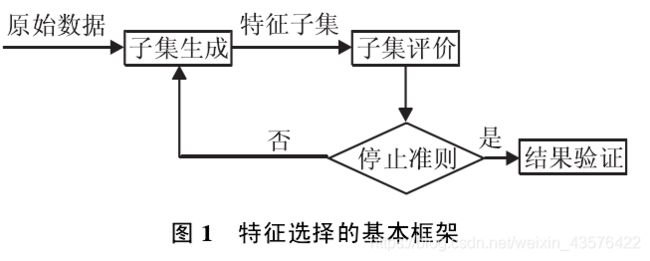
特征选择的一般过程：

1. 生成子集：搜索特征子集，为评价函数提供特征子集
2. 评价函数：评价特征子集的好坏
3. 停止准则：与评价函数相关，一般是阈值，评价函数达到一定标准后就可停止搜索
4. 验证过程：在验证数据集上验证选出来的特征子集的有效性

由于子集搜索是一个比较费时的步骤,因此下面 给出了另一种特征选择框架, 避免了子集搜索, 可以高效快速地寻找最优子集.

常用方法分类

1. Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。

•   （去掉取值变化小的特征 Removing features with low variance）
  

•   （单变量特征选择 Univariate feature selection）
  

2. Wrapper：封装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。Wrapper这里指不断地使用不同的特征组合来测试学习算法进行特征选择。

•   	递归特征消除 (Recursive Feature Elimination)
  

3. Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小排序选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。

•   使用SelectFromModel选择特征 (Feature selection using SelectFromModel)
  

•   将特征选择过程融入pipeline (Feature selection as part of a pipeline)
  

sklean的例子

https://scikit-learn.org/stable/modules/feature_selection.html#feature-selection

去掉取值变化小的特征 Removing features with low variance

方差选择法
方差保持是特征选择的简单基线方法。它删除方差不符合某些阈值的所有要素。默认情况下，它删除所有零方差要素，即在所有样本中具有相同的值的要素。

例如，假设我们有一个包含布尔要素的数据集，并且我们希望删除超过 80% 的示例中的 1 或 0（开或 关）的所有要素。布尔要素是伯努利随机变量，这些变量的方差由下式给出：
$$Var[X]=p(1-p)$$

因此，我们可以选择使用阈值：.8 * (1 - .8)

>>> from sklearn.feature_selection import VarianceThreshold
>>> X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
>>> sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
>>> sel.fit_transform(X)
array([[0, 1],
       [1, 0],
       [0, 0],
       [1, 1],
       [1, 0],
       [1, 1]])

如预期的那样，VarianceThreshold已经删除了第一列。

递归特征消除法

递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征的代码如下：

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

#递归特征消除法，返回特征选择后的数据
#参数estimator为基模型
#参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)

基于学习模型的特征排序 (Model based ranking)

这种方法的思路是直接使用你要用的机器学习算法，针对每个单独的特征和响应变量建立预测模型。其实Pearson相关系数等价于线性回归里的标准化回归系数。假如某个特征和响应变量之间的关系是非线性的，可以用基于树的方法（决策树、随机森林）、或者扩展的线性模型等。基于树的方法比较易于使用，因为他们对非线性关系的建模比较好，并且不需要太多的调试。但要注意过拟合问题，因此树的深度最好不要太大，再就是运用交叉验证。

在波士顿房价数据集上使用sklearn的随机森林回归给出一个单变量选择的例子：

from sklearn.cross_validation import cross_val_score, ShuffleSplit
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor

#Load boston housing dataset as an example
boston = load_boston()
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]

rf = RandomForestRegressor(n_estimators=20, max_depth=4)
scores = []
for i in range(X.shape[1]):
     score = cross_val_score(rf, X[:, i:i+1], Y, scoring="r2",
                              cv=ShuffleSplit(len(X), 3, .3))
     scores.append((round(np.mean(score), 3), names[i]))
print sorted(scores, reverse=True)

参考：结合Scikit-learn介绍几种常用的特征选择方法，
https://www.cnblogs.com/hhh5460/p/5186226.html