Tarjan缩点算法

欢迎访问个人博客

概述

强连通分量

  强连通图（$\text{Strongly Connected Graph}$）是指在有向图 $G$ 中，如果对于每一对 $v_i,v_j$，$v_i\ne v_j$，从 $v_i$ 到$v_j$和从 $v_j$ 到 $v_i$ 都存在路径，则称 $G$ 是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。
（来源：百度百科）

  如上图所示，由节点$1,2,3$构成的环组成一个强连通分量。

算法思路

  $\text{Tarjan}$算法（以发现者$\text{Robert Tarjan}$命名）是一个在图中查找强连通分量的算法。
  此算法以一个有向图作为输入，并按照所在的强连通分量给出其顶点集的一个划分。图中的每个节点只在一个强连通分量中出现，即使是在有些节点单独构成一个强连通分量的情况下（比如图中出现了树形结构或孤立节点）。
  算法的基本思想如下：任选一节点开始进行深度优先搜索（若深度优先搜索结束后仍有未访问的节点，则再从中任选一点再次进行）。搜索过程中已访问的节点不再访问。搜索树的若干子树构成了图的强连通分量。
  节点按照被访问的顺序存入堆栈中。从搜索树的子树返回至一个节点时，检查该节点是否是某一强连通分量的根节点并将其从堆栈中删除。如果某节点是强连通分量的根，则在它之前出堆栈且还不属于其他强连通分量的节点构成了该节点所在的强连通分量。
（来源：$\text{WikiPedia}$）
  我们维护两个重要的数组$dfn[i]$和$low[i]$。
  $dfn[i]$是一个时间戳，代表节点$i$被遍历到的次序，时间戳不可改变。
  $low[i]$代表该子树中，且仍在栈中的最小时间戳，$low[]$相等的点在同一强连通分量中。
  每次搜索要初始化dfn[x]=low[x]=++timer（$timer$初始值为$0$），  每一个节点本身可视为一个强连通分量，因此将$low[x]$暂时赋予时间戳，在搜索子树的过程中更新$low[x]$。
  当无法继续搜索时，如果$dfn[x]=low[x]$，说明找到了一个强连通分量。

过程模拟

  给一张有向图。

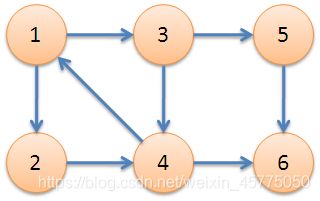
  从节点$1$开始$\text{DFS}$，把遍历到的节点加入栈中。搜索到节点$x=6$时就无法向下继续搜索，$dfn[6]=low[6]$，找到了一个强连通分量。退栈直到栈顶元素为$x$为止，于是找到 $\{6\}$ 为一个强连通分量。

  返回节点$5$，发现$dfn[5]=low[5]$，退栈后 $\{5\}$ 为一个强连通分量。

  返回节点$3$，继续搜索到节点$4$，把$4$加入堆栈。发现节点$4$向节点$1$有后向边，节点$1$还在栈中，所以$low[4]=1$。返回$3$，$3$还在栈中，更新$low[3]=1$。

  继续回到节点$1$，最后访问节点$2$。$4$还在栈中，所以更新$low[2]=5$。返回$1$后，发现$dfn[1]=low[1]$，把栈中节点全部取出，组成一个连通分量 $\{1,3,4,2\}$ 。

  至此，算法结束，求出了图中全部的三个强连通分量 $\{1,3,4,2\},\{5\},\{6\}$。
  可以发现，运行$\text{Tarjan}$算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为$O(N+M)$。
  注意：$\text{Tarjan}$算法一遍不一定能搜完所有的点。所以我们要对一趟跑下来还没有被访问到的点继续跑$\text{Tarjan}$，判断依据就是看$dfn[i]$是否为$0$。

模板

Tarjan缩点

int n,m;//点数，边数 
int timer;//dfs时间戳 
int stack[N],top;//栈 
int deg[N];//新建图的度 
int dfn[N],low[N]; 
bool instack[N];//是否在栈中 
int head[N],tot;//链式前向星 
int cnt;//强连通分量个数
int belong[N];//所属将连通分量编号
void tarjan(int x)
{
     
	dfn[x]=low[x]=++timer;//给时间戳
	//入栈 
	stack[++top]=x;
	instack[x]=1;
	int i;
	/*----------------------更新---------------------*/ 
	for(i=head[x];i;i=edge[i].Next)
	{
     
		int y=edge[i].to;
		if(!dfn[y])
		{
     
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(instack[y]) low[x]=min(low[x],dfn[y]);
	}
	/*---------------------------------------------*/
	if(dfn[x]==low[x])
	{
     
		int y;
		//找到一个强连通分量 
		cnt++;  
		do  
		{
       
			//退栈
			y=stack[top--];  
			instack[y]=false;  
			belong[y]=cnt;//给点赋值所在的强连通分量编号  
		}while(x!=y);  
	} 
}

洛谷 P3387 【模板】缩点

$\text{Enter}$

题目背景

  缩点+DP

题目描述

  给定一个 $n$ 个点 $m$ 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。
  允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

输入格式

  第一行两个正整数 $n,m$
  第二行 $n$ 个整数，依次代表点权
  第三至 $m+2$ 行，每行两个整数 $u,v$，表示一条 $u\to v$ 的有向边。

输出格式

  共一行，最大的点权之和。

输入输出样例

输入 #1

2 2
1 1
1 2
2 1

输出 #1

2

说明/提示

【数据范围】
  对于 $100\%$ 的数据，$1\le n\le 10^4$，$1\le m\le 10^5$，点权 $\in [0,1000]$
  算法：$\text{Tarjan}$ 缩点 $\text{+}$ $\text{DAGdp}$

代码

#include
#include
#include
#include
#define N 10005
using namespace std;
int n,m;//点数，边数 
int timer;//dfs时间戳 
int stack[N],top;//栈 
int deg[N];//新建图的度 
int dfn[N],low[N]; 
bool instack[N];//是否在栈中 
int head[N],tot;//链式前向星 
int p[N];//点权 
int val[N];//val[i]代表以节点i结束的路径的最大点权值和 
int representative[N];//环的代表元素 
int new_head[N],new_tot;//新的链式前向星 
struct E
{
     
	int from;
	int to;
	int Next;
};
E edge[N*10],new_edge[N*10];
void add(int u,int v)
{
     
	tot++;
	edge[tot].to=v;
	edge[tot].from=u;
	edge[tot].Next=head[u];
	head[u]=tot;
}
void tarjan(int x)
{
     
	dfn[x]=low[x]=++timer;//给时间戳
	//入栈 
	stack[++top]=x;
	instack[x]=1;
	int i;
	/*----------------------更新---------------------*/ 
	for(i=head[x];i;i=edge[i].Next)
	{
     
		int y=edge[i].to;
		if(!dfn[y])
		{
     
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(instack[y]) low[x]=min(low[x],dfn[y]);
	}
	/*---------------------------------------------*/
	if(dfn[x]==low[x])
	{
     
		int y;
		//找到一个强连通分量 
		do
		{
     
			//将x作为这个强连通分量的代表元素 
			y=stack[top--];
			representative[y]=x;
			instack[y]=0;//逐个退栈 
			if(x!=y) p[x]+=p[y];//将一个环的值压到一个点上 
		}while(x!=y);//走完强连通分量后退出 
	} 
}
int toposort()
{
     
	queue<int>q;
	int i;
	//将入度为0的点压入队列 
	for(i=1;i<=n;i++)
	{
     
		if(representative[i]==i&&!deg[i])
		{
     
			q.push(i);
			val[i]=p[i];
		}
	}
	while(!q.empty())
	{
     
		int x=q.front();
		q.pop();
		for(i=new_head[x];i;i=new_edge[i].Next)
		{
     
			int y=new_edge[i].to;
			//简单的DAG上dp 
			val[y]=max(val[y],val[x]+p[y]);
			deg[y]--;//入度减一 
			if(!deg[y]) q.push(y);//退出队列 
		}
	}
	int ans=0;
	for(i=1;i<=n;i++) ans=max(ans,val[i]);
	printf("%d\n",ans);
}
void init()//初始化  
{
     
	tot=0;
	timer=0;
	top=0;
	new_tot=0;
	memset(head,0,sizeof(head));
	memset(dfn,0,sizeof(dfn));
	memset(instack,0,sizeof(instack));
	memset(deg,0,sizeof(deg));
	memset(new_head,0,sizeof(new_head));
	memset(representative,0,sizeof(representative));
	memset(val,0,sizeof(val));
}
void solve()
{
     
	init();
	scanf("%d%d",&n,&m);
	int i;
	for(i=1;i<=n;i++) scanf("%d",&p[i]);
	for(i=1;i<=m;i++)
	{
     
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);
	}
	for(i=1;i<=n;i++) 
	{
     
		if(!dfn[i]) 
		{
     
			tarjan(i);
		}
	}
	//建立新的图 
	for(i=1;i<=m;i++)
	{
     
		//取一条边的两点，如果代表元素不同说明不是同一个环，可以相连	 
		int x=representative[edge[i].from];
		int y=representative[edge[i].to];
		if(x!=y)
		{
     
			new_edge[++new_tot].from=x;
			new_edge[new_tot].to=y;
			new_edge[new_tot].Next=new_head[x];
			new_head[x]=new_tot;
			deg[y]++;//统计每个点的入度 
		}
	}
	//用拓扑序作为dp顺序 
	toposort();
}
int main()
{
     
	solve();
	return 0;
}