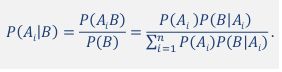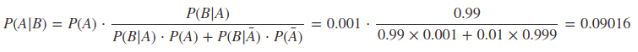C4: 贝叶斯公式及其应用

》》点赞，收藏+关注，理财&技术不迷路《《

P(A,B)=P(A|B)⋅P(B)=P(B|A)⋅P(A)

通过移项，我们可以得到：

P(A|B)= P(B|A)⋅P(A) / P(B)

这个就是我们的贝叶斯公式的雏形，我们暂时不分析这个公式，我们来看看先验概率prior probability和后验概率posterior probability。我们知道P(A|B)是在 B 发生的情况下 A 发生的可能性：

首先，事件B发生之前，我们对事件A的发生有一个基本的概率判断，称为A的先验概率，用P(A)表示；

其次，事件B发生之后，我们对事件A的发生概率重新评估，称为A的后验概率，用

P(A|B)表示；

类似的，事件A发生之前，我们对事件B的发生有一个基本的概率判断，称为B的先验概率，用P(B)表示；

同样，事件A发生之后，我们对事件B的发生概率重新评估，称为B的后验概率，用

P(B|A)表示。

计学上有两大派系：

概率学派是从事件的随机性出发以样本空间的研究为核心；

贝叶斯学派则从观察者的角度出发，他们认为样本空间是固定的，事件的随机性不过是观察者掌握信息不完备所造成的， 观察者所掌握的信息多寡将影响观察者对于事件的认知。

贝叶斯公式将事物刻画的更加有“人情味”，这让繁琐的数学变得有趣了起来。今天我们一起来入门贝叶斯公式， 揭示事物背后的合理性。

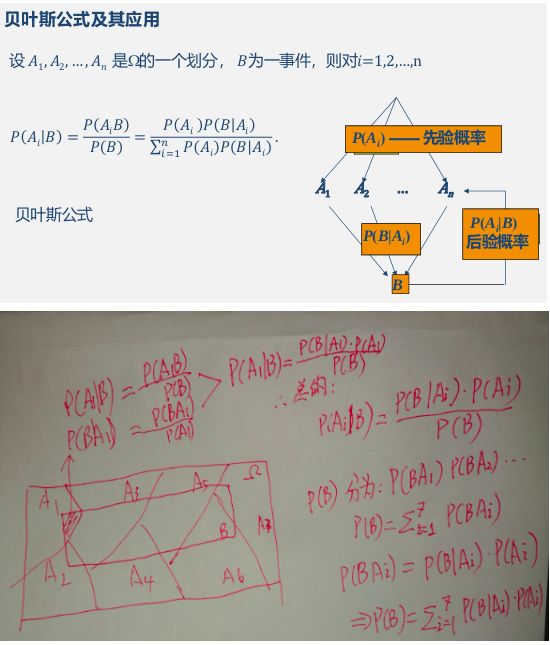
将事件B进行分割的时候，不是直接对B进行分割，而是先找到样本空间Ω的一个个划分为A1,A2,A3...,这样事件A就被事件BA1,BA2,BA3....分解成了n部分，即

描述一个事件，往往会有相应的事件伴随着发生考虑的全面点，已有的知识充分利用上才是贝叶斯后验概率的精髓。　我们接下来为了分析的简单一些，都是用公式1作为基础分析展开。我们看公式P(A|B)=P(B|A)⋅P(A) / P(B)，我习惯这样来看贝叶斯公式， ，这时候可以将贝叶斯公式看为两个部分，第一部分是先验概率P(A)，后一部分是“调整因子”。

我们详细点说就是把P(A)称为”先验概率”（Prior probability），即在B事件发生之前，我们对A事件概率的一个判断。P(A|B)称为”后验概率”（Posterior probability）， 即在B事件发生之后，我们对A事件概率的重新评估。P(B|A) / P(B)称为”可能性函数”（Likelyhood），这是一个调整因子，使得预估概率更接近真实概率。

　　所以，条件概率可以理解成下面的式子：

后验概率　＝　先验概率×调整因子（标准似然度）

Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。

Pr(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。

Pr(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。

Pr(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）。

按这些术语，Bayes法则可表述为：

后验概率 = (似然度 * 先验概率)/标准化常量　也就是说，后验概率与先验概率和似然度的乘积成正比。

另外，比例Pr(B|A)/Pr(B)也有时被称作标准似然度（standardised likelihood）

贝式定理

    P(A,B)=P(A|B)⋅P(B)=P(B|A)⋅P(A)

对于变量有二个以上的情况，贝式定理亦成立。例如：

P(A|B,C) = P(A,B,C)/P(B,C)

  = P(C|A,B)*P(A,B)/P(B,C)

 = P(C|A,B)*P(B|A)*P(A)/P(C|B)*P(B)

这个式子可以由套用多次二个变量的贝氏定理及条件机率的定义导出。

这就是贝叶斯推断的含义。我们先预估一个”先验概率”，然后加入实验结果，看这个实验到底是增强还是削弱了”先验概率”，由此得到更接近事实的”后验概率”。

在这里，如果”可能性函数” P(B|A) / P(B)>1，意味着”先验概率”被增强，事件A的发生的可能性变大；如果”可能性函数”=1，意味着B事件无助于判断事件A的可能性； 如果”可能性函数”<1，意味着”先验概率”被削弱，事件A的可能性变小。

　　有了以上对贝叶斯公式的分析，我们回过头来看看之前提到的那个没有解决的检测阳性情况下得病概率的计算。回顾一下，我们用 A 表示这个人患有该疾病， 用 B 表示医院检测的结果是阳性，表示A的补集也就是这个人未得该病，道我们已经有了茫茫人海中得病概率P(A) = 0.001的先验概率,也有了得病情况下为阳性的概率 P(B|A)=0.99，在分析中我们知道被检测者未患病的概率P()=0.999，已知未患病的情况下检测为阳性的概率P(B|)=0.01。 现在我们要计算的就是在阳性情况下得病的概率，即为在已知检测结果为阳性的情况下得病的后验概率 P(A|B)是多少?

我们利用贝叶斯公式来算了：

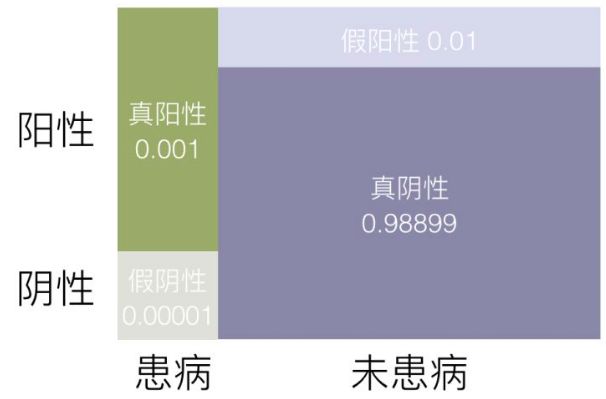
通过计算我们得到，在这个前提下即使你检测出的是阳性，你得这个病的概率也仅为9%左右，所以，在医学没达到完美的情况下都是存在着一定的误差的。 即使你查出了阳性你仍然有很大概率是没有得病的，为了确定往往需要复查，这种情况就是我们常常提及的假阳性，我们通过图看一下。

从贝叶斯的角度来看，随意选取的一个被测者，由于信息并不充分，未检测之前有假阳性、真阳性、假阴性和真阴性四种可能，这些可能性由检测技术和该疾病的感染率决定， 当检测结果为阳性的时候，只剩下真阳性和假阳性两种可能，而真阳性的概率仅为假阳性的十分之一，贝叶斯公式在这里的实际意义是：

即使被医院检测为阳性，实际患病的概率其实还不到10%，有很大可能是假阳性，往往需要复检来确定是否真的患病，让我们再来计算初检和复检结果都为阳性时， 患病的可能性。假设两次检查的准确率相同，都是99%，这里令 B 为第一次检测结果为阳性，C 为第二次检测结果为阳性，A 为被检测者患病， 那么两次检测结果都是阳性患病的概率可以表示为：

可见复检结果大大提高了检测的可信度，联系上面的图，复检的意义在于大幅减少假阳性的可能（0.01 -> 0.0001）从而提高阳性检测的准确性.