Linked List(easy五道题)(medium四道题)
easy
206. Reverse Linked List
Reverse a singly linked list.
Example:
Input: 1->2->3->4->5->NULL Output: 5->4->3->2->1->NULL
Follow up:
A linked list can be reversed either iteratively or recursively. Could
you implement both?
In-place iterative and recursive Java solution:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
/* iterative solution */
ListNode newHead = null;
while (head != null) {
ListNode next = head.next;
head.next = newHead;
newHead = head;
head = next;
}
return newHead;
}
public ListNode reverseList(ListNode head) {
/* recursive solution */
return reverseListInt(head, null);
}
private ListNode reverseListInt(ListNode head, ListNode newHead) {
if (head == null)
return newHead;
ListNode next = head.next;
head.next = newHead;
return reverseListInt(next, head);
}
}
21. Merge Two Sorted Lists
Merge two sorted linked lists and return it as a new list. The new
list should be made by splicing together the nodes of the first two
lists.Example:
Input: 1->2->4, 1->3->4 Output: 1->1->2->3->4->4
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2){
if(l1 == null) return l2;
if(l2 == null) return l1;
if(l1.val < l2.val){
l1.next = mergeTwoLists(l1.next, l2);
return l1;
} else{
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
}
}
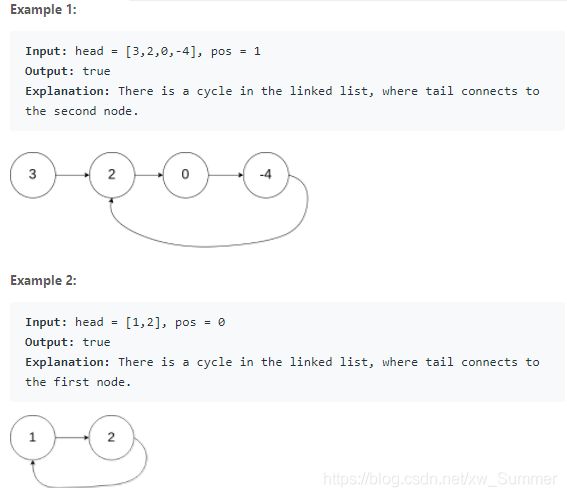
141. Linked List Cycle
Given a linked list, determine if it has a cycle in it.
To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.
Follow up:Can you solve it using O(1) (i.e. constant) memory?
O(1) Space Solution:
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
if(head==null) return false;
ListNode walker = head;
ListNode runner = head;
while(runner.next!=null && runner.next.next!=null) {
walker = walker.next;
runner = runner.next.next;
if(walker==runner) return true;
}
return false;
}
}
解释: Use two pointers, walker and runner. walker moves step by step. runner
moves two steps at time. if the Linked List has a cycle walker and
runner will meet at some point.
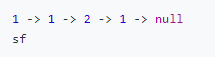
234. Palindrome Linked List
Given a singly linked list, determine if it is a palindrome.
Example 1:
Input: 1->2 Output: false
Example 2:
Input: 1->2->2->1 Output: true
Follow up: Could you do it in O(n) time and O(1) space?
Reversing a list is not considered “O(1) space”
It is a common misunderstanding that the space complexity of a program is just how much the size of additional memory space being used besides input. An important prerequisite is neglected the above definition: the input has to be read-only. By definition, changing the input and change it back is not allowed (or the input size should be counted when doing so). Another way of determining the space complexity of a program is to simply look at how much space it has written to. Reversing a singly linked list requires writing to O(n) memory space, thus the space complexities for all “reverse-the-list”-based approaches are O(n), not O(1).
Solving this problem in O(1) space is theoretically impossible due to two simple facts: (1) a program using O(1) space is computationally equivalent to a finite automata, or a regular expression checker; (2) the pumping lemma states that the set of palindrome strings does not form a regular set.
Please change the incorrect problem statement.
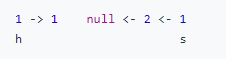
Java, easy to understand:
This can be solved by reversing the 2nd half and compare the two
halves. Let’s start with an example [1, 1, 2, 1].In the beginning, set two pointers fast and slow starting at the head.
(1) Move: fast pointer goes to the end, and slow goes to the middle.
(2)
Reverse: the right half is reversed, and slow pointer becomes the 2nd head.
(3) Compare: run the two pointers head and slow together and compare.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isPalindrome(ListNode head) {
ListNode fast = head, slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
if (fast != null) { // odd nodes: let right half smaller
slow = slow.next;
}
slow = reverse(slow);
fast = head;
while (slow != null) {
if (fast.val != slow.val) {
return false;
}
fast = fast.next;
slow = slow.next;
}
return true;
}
public ListNode reverse(ListNode head) {
ListNode prev = null;
while (head != null) {
ListNode next = head.next;
head.next = prev;
prev = head;
head = next;
}
return prev;
}
}
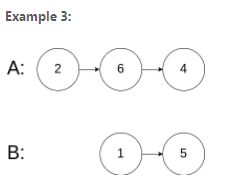
160. Intersection of Two Linked Lists
Write a program to find the node at which the intersection of two
singly linked lists begins.For example, the following two linked lists:
begin
to intersect at node c1.Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
Output: Reference of the node with value = 8
Input Explanation: The intersected node’s value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it
reads as [4,1,8,4,5]. From the head of B, it reads as [5,0,1,8,4,5].
There are 2 nodes before the intersected node in A; There are 3 nodes
before the intersected node in B.Input: intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Reference of the node with value = 2
Input Explanation: The intersected node’s value is 2 (note that this must not be 0 if the two lists intersect). From the head of A, it
reads as [0,9,1,2,4]. From the head of B, it reads as [3,2,4]. There
are 3 nodes before the intersected node in A; There are 1 node before
the intersected node in B.Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: null Input Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do
not intersect, intersectVal must be 0, while skipA and skipB can be
arbitrary values.
Explanation: The two lists do not intersect, so return null.Notes:
If the two linked lists have no intersection at all, return null. The linked lists must retain their original structure after the function returns. You may assume there are no cycles anywhere in the entire linked structure. Your code should preferably run in O(n) time and use only O(1) memory.
Java solution without knowing the difference in len:
I found most solutions here preprocess linkedlists to get the difference in len. Actually we don’t care about the “value” of difference, we just want to make sure two pointers reach the intersection node at the same time.
We can use two iterations to do that. In the first iteration, we will reset the pointer of one linkedlist to the head of another linkedlist after it reaches the tail node. In the second iteration, we will move two pointers until they points to the same node. Our operations in first iteration will help us counteract the difference. So if two linkedlist intersects, the meeting point in second iteration must be the intersection point. If the two linked lists have no intersection at all, then the meeting pointer in second iteration must be the tail node of both lists, which is null
Below is my commented Java code:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
//boundary check
if(headA == null || headB == null) return null;
ListNode a = headA;
ListNode b = headB;
//if a & b have different len, then we will stop the loop after second iteration
while( a != b){
//for the end of first iteration, we just reset the pointer to the head of another linkedlist
a = a == null? headB : a.next;
b = b == null? headA : b.next;
}
return a;
}
}
medium
2. Add Two Numbers
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
public class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode c1 = l1;
ListNode c2 = l2;
ListNode sentinel = new ListNode(0);
ListNode d = sentinel;
int sum = 0;
while (c1 != null || c2 != null) {
sum /= 10;
if (c1 != null) {
sum += c1.val;
c1 = c1.next;
}
if (c2 != null) {
sum += c2.val;
c2 = c2.next;
}
d.next = new ListNode(sum % 10);
d = d.next;
}
if (sum / 10 == 1)
d.next = new ListNode(1);
return sentinel.next;
}
}
Improved. O(1) space complexity Java solution if the interviewer agree with modification of list1.
Step1: sum curr1+ curr2, update carry,
Step 2: update curr1,
Step 3: if curr1.next == null, connect two list, therefore, we only need 1 pointer.
Step 4,5: update the remainder list and add 1 at last.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
if(l1 == null) return l2;
else if(l2 == null) return l1;
ListNode dummy = new ListNode(0);
ListNode curr1 = dummy;
curr1.next = l1;
ListNode curr2 = new ListNode(0);
curr2.next = l2;
int carry = 0;
while(curr1.next != null && curr2.next != null){ //1. add curr1 and curr2, update carry
curr1 = curr1.next;
curr2 = curr2.next;
int sum = curr1.val + curr2.val + carry;
carry = sum / 10;
curr1.val = sum % 10; //2. O(1) space complexity by update only curr1
if(curr1.next == null && curr2.next != null){//3. if the length of l1 is shorter, connect to l2
curr1.next = curr2.next; // E.g. l1: 2-4; l2:5,6,5
break;
}
}
while(curr1.next != null && carry == 1){ //4. update the ListNode if carry == 1
curr1 = curr1.next;
int sum = curr1.val + carry;
carry = sum / 10;
curr1.val = sum % 10;
}
if(carry == 1){ //5. add ListNode(1) at last
curr1.next = new ListNode(1);
}
return dummy.next;
}
}
19. Remove Nth Node From End of List
Given a linked list, remove the n-th node from the end of list and return its head.
Note:
Given n will always be valid.
Follow up:
Could you do this in one pass?
Simple Java solution in one pass:
A one pass solution can be done using pointers. Move one pointer fast --> n+1 places forward, to maintain a gap of n between the two pointers and then move both at the same speed. Finally, when the fast pointer reaches the end, the slow pointer will be n+1 places behind - just the right spot for it to be able to skip the next node.
Since the question gives that n is valid, not too many checks have to be put in place. Otherwise, this would be necessary.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode start = new ListNode(0);
ListNode slow = start, fast = start;
slow.next = head;
//Move fast in front so that the gap between slow and fast becomes n
for(int i=1; i<=n+1; i++) {
fast = fast.next;
}
//Move fast to the end, maintaining the gap
while(fast != null) {
slow = slow.next;
fast = fast.next;
}
//Skip the desired node
slow.next = slow.next.next;
return start.next;
}
}
142. Linked List Cycle II
Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.
Note: Do not modify the linked list.
Follow up:
Can you solve it without using extra space?
Java O(1) space solution with detailed explanation:
Define two pointers slow and fast. Both start at head node, fast is twice as fast as slow. If it reaches the end it means there is no cycle, otherwise eventually it will eventually catch up to slow pointer somewhere in the cycle.
Let the distance from the first node to the the node where cycle begins be A, and let say the slow pointer travels travels A+B. The fast pointer must travel 2A+2B to catch up. The cycle size is N. Full cycle is also how much more fast pointer has traveled than slow pointer at meeting point.
A+B+N = 2A+2B
N=A+B
From our calculation slow pointer traveled exactly full cycle when it meets fast pointer, and since originally it travled A before starting on a cycle, it must travel A to reach the point where cycle begins! We can start another slow pointer at head node, and move both pointers until they meet at the beginning of a cycle.
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
if (fast == slow){
ListNode slow2 = head;
while (slow2 != slow){
slow = slow.next;
slow2 = slow2.next;
}
return slow;
}
}
return null;
}
}
148. Sort List
Sort a linked list in O(n log n) time using constant space complexity.
Java merge sort solution:
public class Solution {
public ListNode sortList(ListNode head) {
if (head == null || head.next == null)
return head;
// step 1. cut the list to two halves
ListNode prev = null, slow = head, fast = head;
while (fast != null && fast.next != null) {
prev = slow;
slow = slow.next;
fast = fast.next.next;
}
prev.next = null;
// step 2. sort each half
ListNode l1 = sortList(head);
ListNode l2 = sortList(slow);
// step 3. merge l1 and l2
return merge(l1, l2);
}
ListNode merge(ListNode l1, ListNode l2) {
ListNode l = new ListNode(0), p = l;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
p.next = l1;
l1 = l1.next;
} else {
p.next = l2;
l2 = l2.next;
}
p = p.next;
}
if (l1 != null)
p.next = l1;
if (l2 != null)
p.next = l2;
return l.next;
}
}