线性代数(4)：QR分解原理，矩阵在图上面的应用，正交向量，子空间，最小二乘法...

rank(AAT)=rank(A)rank(AA^T)=rank(A)rank(AAT)=rank(A),rank是矩阵的秩的意思。
投影矩阵有什么用？因为Ax=b很可能没有解，但是没有解我们可以求最接近的解啊。所以要把b投影到A的列向量空间中。为何要投影到A的向量空间中？因为Ax它的本质就是对A的列向量进行线性组合，而线性组合就是向量空间。如果我们能把b投影到A的向量空间中。

假设Ax^A\hat xAx^是b在A列向量空间上的投影，那么p=(Ax^−b)p=(A\hat x-b)p=(Ax^−b)，其中$p$是误差向量。我们知道Ax^A\hat xAx^是A的列向量空间中的一个向量，并且Ax^A\hat xAx^是b在A列向量空间上的投影。那么p=(Ax^−b)p=(A\hat x-b)p=(Ax^−b)垂直于A的列向量空间。如下图所示：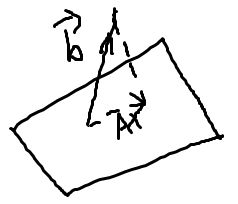

现在我们证明下ATAx^=ATbA^TA \hat x=A^TbATAx^=ATb
根据p=(Ax^−b)p=(A\hat x-b)p=(Ax^−b)垂直于A的列向量空间，所以AT(Ax^−b)=0A^T(A\hat x-b)=0AT(Ax^−b)=0，所以ATAx^=ATbA^TA\hat x=A^TbATAx^=ATb，证明完毕。

b投影到A列向量空间的投影矩阵：p=(ATA)−1ATbp=(A^TA)^{-1}A^Tbp=(ATA)−1ATb
如果A列向量相互独立那么ATAA^TAATA可逆。
证明参考：MIT线性代数.
最小二乘法容易受到离群点影响。
标准正交化A可以使得，ATA=IA^TA=IATA=I
正交矩阵可以是长方形阵。
标准化正交矩阵的用处：

1. QQT=QQTQQTQQ^T=QQ^TQQ^TQQT=QQTQQT
2. 投影矩阵：Q(QTQ)−1QT=QQTQ(Q^TQ)^{-1}Q^T=QQ^TQ(QTQ)−1QT=QQT,如果Q是方阵的话投影矩阵就是I。
3. QTQx=QTb→x=QTb→xi=qiTbQ^TQx=Q^Tb \rightarrow x=Q^Tb \rightarrow x_i = q_i^TbQTQx=QTb→x=QTb→xi​=qiT​b，这意味着b在Q列向量空间内的投影是qiTbq_i^TbqiT​b，也就是说只用与基内积即可。

Gram-schmidt正交法的本质是减去在其他基上的投影，那么剩下的就是垂直部分的分量（垂直就是正交的意思）

我们知道Gram-schmidt正交法来正交化b是这样写的b^=b−(bTa)aaTa\hat b=b-\frac {(b^Ta)a}{a^Ta}b^=b−aTa(bTa)a​。但是为什么这么写呢？那就得回答正交化做了一个怎样的事。正交化就是让原先的几个向量变得相互垂直（正交就是垂直的意思）。我只需要减去当前这个向量在其他基上的投影分量就可以。b在a上面的投影分量是啥？首先这个分量一定是和a同方向，其次它的模一定是$|b|cos\theta$，其中$\theta$是b与a的夹角。所以b在a的投影分量为(∣b∣cosθ)a∣a∣\frac {(|b|cos\theta) a}{|a|}∣a∣(∣b∣cosθ)a​。而cosθ=bTa∣b∣∣a∣cos\theta=\frac {b^Ta}{|b||a|}cosθ=∣b∣∣a∣bTa​。所以b在a的投影分量转换为(bTa)aaTa\frac {(b^Ta)a}{a^Ta}aTa(bTa)a​

QR分解与Gram-schmidt正交法的关系

Gram-schmidt正交法可以把矩阵A列向量都正交化，假设正交化后的矩阵是Q（它是正交矩阵因为各个列向量相互正交）。现在Q可以视作A矩阵损失了一些值后的矩阵。因为Q把A各个列向量同方向的分量都消除了。所以A=QR，其中R是补回那些损失两的矩阵。接下来我们看看那个R矩阵长啥样。
现在已知 A=[a,b]=QR=[q1,q2]RA=[a,b]=QR=[q_1,q_2]RA=[a,b]=QR=[q1​,q2​]R，其中q1,q2q_1,q_2q1​,q2​是列向量$a,b$正交化后的向量。R取多少怎么让这个等式成立呢？看下面这个矩阵：
$A=[a,b]=QR=[q1,q2]R=[q1,q2][q1Taq1Tbq2Taq2Tb]A=[a,b]=QR=[q_1,q_2]R=[q_1,q_2]\begin{bmatrix} q_1^Ta & q_1^Tb \\ q_2^Ta & q_2^Tb \end{bmatrix}A=[a,b]=QR=[q1​,q2​]R=[q1​,q2​][q1T​aq2T​a​q1T​bq2T​b​]
为何R这么设计呢？因为q1q_1q1​与q2q_2q2​一定正交，而与q1q_1q1​则同方向。所以q1q2Tbq_1q_2^Tbq1​q2T​b等于0. q1q1Ta=aq_1q_1^Ta=aq1​q1T​a=a

用“点-边”矩阵表示电流图

假如有下面这个电流图（当然也可以表示其他的意义比如河流，建筑受力）：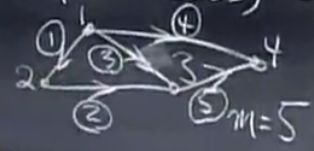

然后我们构造一个矩阵来描述这个图，数学家把这个矩阵叫做关联矩阵（incident Matrix）：
其中每行代表一条边，每列代表一个节点。第i行第j列的元素表示，第i条边是否包含第j个节点，并且这个节点是流入(1)还是流出(-1)。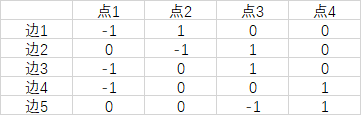

行向量线性组合代表什么意义？

如果我们对行向量进行线性组合，那么可以分析出是否存在环路。如果存在环路肯定意味着那几行的点出去的电流等于进来的电流。即行向量线性组合为0.于是我们可以根据行向量是否线性相关来判断当前这个图到底有没有环路。

列向量线性组合代表什么意义？

列向量的线性组合即Ax=0.我们可以把x视作电动势，那么各个节点的电动势之和等于0.这意味着，整个节点网络是的电动势是0.这意味着没有外来电压输入。如果是Ax=b那么外来电压就是b。

转载于:https://www.cnblogs.com/ailitao/p/11047275.html