字符串匹配KMP算法详解（这可能是东半球最好理解的解释）

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。

累赘一下，KMP算法是字符串匹配算法，比如搜索字符串“abcdefg”中是否含有子串“bcd”。

1、KMP算法引入

假设给你两个字符串strOne=“abababaabc”、strTwo = “ababaab”，要求你判断strOne字符串中是否含有子串strTwo。

可能你的第一反映是，遍历一遍strOne，依次搜索strTwo，时间复杂度为O(m*n)级别（m、n分别为两个字符串的长度）。也就是俗称的暴搜法，而KMP算法是一种时间复杂度在O(m+n)级别的高效算法。

暴力匹配伪代码

//第一层循环，依次设置strOne字符串中的匹配起始下标
//注：m为strOne的长度，n为strTwo的长度
for (int i = 0; i < m - n; ++i) {
     
	int j = 0;
	//从strOne[i]处开始匹配字符串strTwo
	while (j < n && strOne[i + j] == strTwo[j]) {
     
		j += 1;
	}
	//j到达strTwo的尾端时，说明在strOne[i]处开始，成功匹配到了一个strTwo子串 
	if (j == n) {
     
		cout << "strOne中包含子串strTwo" << endl;
		break;
	}
}
//如果蛮力法都看不懂，那我真的没办法了。。。

在介绍KMP算法前，我们先搞明白暴搜法费劲的地方在哪里。

下标：	  0123456789
strOne = "abababaabc"
strTwo = "ababaab"

根据蛮力法的思路，
第一轮匹配：当i = 0为strOne的起始匹配下标时，我们最多能够匹配到j = 4，
也就是我们只能成功匹配strTwo的前5个字符，因为strOne[i + 6] != strTwo[5],

第二轮匹配：接着我们得将i自增1，即i = 1为strOne的起始匹配下标，重新开始匹配
下标：	  0123456789
strOne = "abababaabc"
strTwo =  "ababaab"
显然strOne[i] != strTwo[0]，即j = 0就开始不匹配了

第三轮匹配：接着我们得将i自增1，即i = 2为strOne的起始匹配下标，重新开始匹配
下标：	  0123456789
strOne = "abababaabc"
strTwo =   "ababaab"
根据while循环，此次能完全匹配strTwo，查找成功

缺陷：每次当strOne[i + j] != strTwo[j]时，即匹配不下去（比如，第一、二轮匹配），我们选择调整i自增，然后又重新开始匹配。等于就是说每次我们好不容易成功匹配了几个字符后，突然发生断裂，这时我们需要重头开始做，那之前做的匹配工作能不能利用起来呢？

2、next[i]引入（非常重要）

$next[i]记录字符串str[0,i]相等的最长前后缀的前缀的最后一位下标$

何为字符串前缀，比如字符串str="abab"前缀有"a"、"ab"、"aba"、"abab"
何为字符串后缀，比如字符串str="abab"后缀有"b"、"ab"、"bab"、"abab"
那么str="abab"的相等的最长前、后缀分别为 "ab"、"ab"，前缀"ab"最后一个字符’b’的下标为1，所以字符串str="abab"的next[3] = 1。

$next[i]计算需要排除自身，即前、后缀不能选自己！$

再举几个栗子
比如str="abcda"，str[0, 4] = ”abcda“的最长相等前、后缀分别为"a","a"，即next[4] = 0（前缀"a"最后一位的下标为0）

比如str="abcdab"，str[0, 4] = ”abcda“的最长相等前、后缀分别为"a","a"，即next[4] = 0（前缀"a"最后一位的下标为0）
注意i == 4，限定了子串str[0, 4]的范围"abcda"

比如str="abcdab"，str[0, 5] = ”abcdab“的最长相等前、后缀分别为"ab","ab"，即next[5] = 1（前缀"ab"最后一位的下标为1）

比如str="ababac"，str[0, 4] = ”ababa“的最长相等前、后缀分别为"aba","aba"，即next[4] = 2（前缀"aba"最后一位的下标为2）

比如str="ababac"，str[0, 5] = ”ababac“的最长相等前、后缀分别为"",""，没有满足的前后缀，因此next[5] = -1（也可以理解为空前缀""最后一位的下标为-1）

检验一下你是否理解了next[i]的计算规则，

请计算str="ababa"各个next[i]组成的next数组。
（拿出纸笔来画画呗~）（拿出纸笔来画画呗~）（拿出纸笔来画画呗~）
答案为next[-1, -1, 0, 1, 2]

答							防										当i = 0时，str[0, 0] = "a"，next[i]的最长相等前、后缀分别为"","",
案							偷											注意前后缀不能选自己"a",因此next[0] = -1
在							窥										当i = 1时，str[0, 1] = "ab"，next[i]的最长相等前、后缀分别为"","",
右																		同样前后缀不能选自己"ab",因此next[1] = -1
边																	当i = 2时，str[0, 2] = "aba"，next[i]的最长相等前、后缀分别为"a","a",
																		同样前后缀不能选自己"aba",前缀"a"的最后一个字符下标为0，因此next[2] = 0
请							防										当i = 3时，str[0, 3] = "abab"，next[i]的最长相等前、后缀分别为"ab","ab",
向							偷											同样前后缀不能选自己"abab",前缀"ab"的最后一个字符下标为1，因此next[3] = 1
右							窥										当i = 4时，str[0, 4] = "ababa"，next[i]的最长相等前、后缀分别为"aba","aba",
滑																		同样前后缀不能选自己"ababa",前缀"aba"的最后一个字符下标为2，因此next[4] = 2

																	因此next = [-1, -1, 0, 1, 2]

到目前为止，我们只介绍了next[i]这一个概念，如果你不能正确计算出str="ababa"的next数组，请不要往下看，否则只会越看越迷糊。

3、$next[i]计算方式的优化$

在上面计算str="ababa"各个next[i]时，我们每次都是取出str[0, i]，然后找出最长的相等的前、后缀，才能得到前缀的最后一个字符的下标。仔细思考一下，这里有一个递推公式我们没有发现！

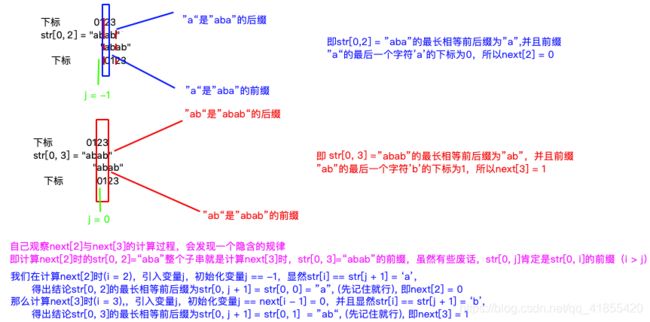
上面的图，我们莫名其妙的映入了变量j，并且两次变量j的初始化都设置的很巧妙，下面我们来解释一下变量j的含义。

变量j的含义

我们引入变量j的主要目的是在计算next[i]时，使用next[i - 1]的成果，找个变量j = next[i - 1]，那么next[i]的值为j + 1，即迭代公式next[i] = next[i - 1] + 1。
但是这个迭代公式使用有一个条件str[i] == str[j + 1],(计算next[3]时i、j的值为i = 3, j = next[i - 1] = next[2] = 0)

也就是说变量j的作用是在计算next[i]的时候，存储str[0, i - 1]的最长相等前后缀的前缀的最后一个字符的下标，即next[i - 1]，即j = next[i - 1]

那么在计算next[2]的时候，为啥j初始化赋值为 -1 呢？
根据上面说的j = next[i - 1] = next[1]，对于str[0, 1] = "ab"，不难计算next[1] == -1吧？

注意，对于任何字符串next[0] = -1，因为字符串string[0, 0]只有一个字符，next[i]的计算时，前后缀不能取自身

得出一个结论，

当str[i] == str[j + 1]时，next[i] = j + 1

结论的证明思路：

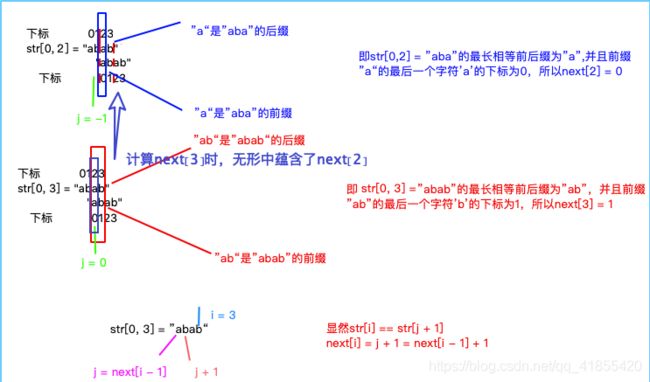
既然结论next[i] = j + 1的使用需要条件str[i] == str[j + 1]。

str[i] ！= str[j + 1]时如何处理？

当str[i] != str[j + 1]，此时就不能利用next[i - 1]的结果了。
比如str = "ababc"，计算next[4]

next数组快速计算代码实现

vector<int> getNexts(const string &str) {
     
    vector<int> next(str.size());
    //对于一个字符的子串，最长相等前后缀为空，赋值为空
    next[0] = -1;
    for (int i = 1, j = -1; i < str.size(); ++i) {
     
        while (j != -1 && str[i] != str[j + 1]) {
     
            //如果str[i] != str[j + 1]，只能一直往前退next[j]
            j = next[j];
        }
        if (str[i] == str[j + 1]) {
     
            //如果有匹配成功了一个字符，则next[i] = j + 1
            //否则next[i] = -1,(匹配不成功的时候j必定-1(否则可以继续j = next[j])，即可赋值next[i] = j = -1,)
            j += 1;
        }
        next[i] = j;
    }
    return next;
}

4、KMP算法

写了这么多的篇幅，终于到了介绍KMP的关键时刻。
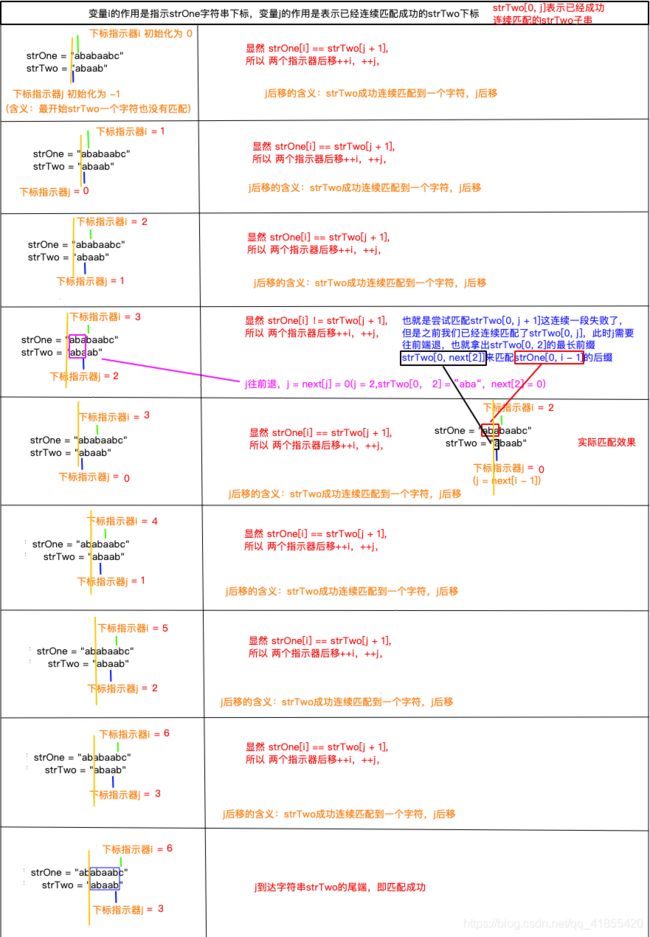
给定示例 strOne = "ababaabc"，strTwo = "abaab"，判断strOne是否包含子串strTwo。

算法的关键：匹配出现断裂如何处理？

算法的重点在第5步，当出现已经匹配完子串strTwo[0, j]，匹配strTwo[j + 1]字符，出现断裂时，此时j倒退到j = next[j]，也就是j倒退到strTwo[0, j]的最长相等前后缀的前缀最后一个字符的下标位置next[j](蛮力法是直接倒退到-1，重新开始匹配。)

那么问题来了，为什么j退到next[j]是最优的呢？

因为我们在将strTwo[j]匹配成功的时候，

strTwo[0, j]这一段已经和strOne[0, i]的后缀匹配成功了。

而strTwo[0, j]的前缀strTwo[0, next[j]]（想一下next[j]的定义，最长相等前、后缀的前缀最后一个字符的下标）

又因为strTwo[0, j]与strOne[0, i]的后缀相等，也就是说strTwo[0, next[j]]是strOne[0, i]的更短的一个后缀。

这就能保证strTwo[0, next[j]]是strTwo当前能够匹配的最长前缀。

假设我们已经将j退回到next[j]的位置，我们还得期望strTwo[j + 1] == strOne[i]，这样我们就能连续匹配strTwo[0, j + 1]，否则我们把j退回就没有什么实质意义。

比如第5步，j回退到next[j] = 0时，由于strTwo[j + 1] == strOne[i]，所以执行完第5的时候，已经成功连续匹配了strTow[0, 1]。

那么问题又来了，j退到next[j]，strTwo[j + 1] != strOne[i]怎么办

前面已多次强调，一直重复赋值j = next[j]（一直后退j），直到出现strTwo[j + 1] == strOne[i]，
如果j = -1还不满足strTwo[j + 1] == strOne[i]，也就是j退到strTwo的起始位置都不满足条件，此时只能后移i，期待后面能匹配成功。

KMP算法的代码实现

//判断字符串strOne是否包含子串strTwo
bool kmp(const string &strOne, const string &strTwo) {
     
    //先计算字符串strTwo的next数组
    vector<int> strTwoNext = getNexts(strTwo);
    for (int i = 0, j = -1; i < strOne.size(); ++i) {
     
        while (j != -1 && strOne[i] != strTwo[j + 1]) {
     
            //如果str[i] != str[j + 1]，只能一直往退j
            j = strTwoNext[j];
        }
        if (strOne[i] == strTwo[j + 1]) {
     
            //匹配成功了一个字符，则j后移
            j += 1;
        }
        if (j == strTwo.size() - 1) {
     
            //j已经到达了strTwo的尾端，说明以及成功连续匹配strTwo
            return true;
        }
    }
    return false;
}

总算是写完了，修改了三四次。。。

KMP算法关键是理解next[j]的定义，j = next[j]的含义，并不怎么难理解。
如果有什么疑问欢迎在评论区讨论。