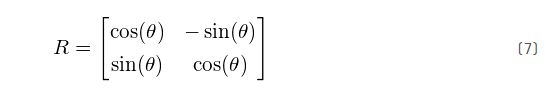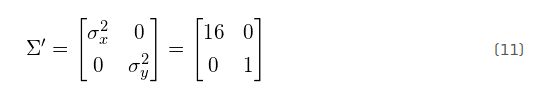协方差矩阵的几何解释

A geometric interpretation of the covariance matrix

http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/

译文：http://demo.netfoucs.com/u010182633/article/details/45937051

转自：https://www.cnblogs.com/jins-note/p/10826272.html

介绍

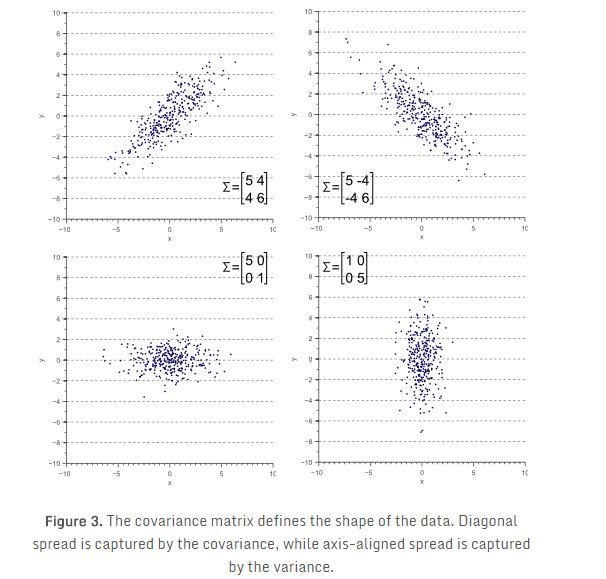
在本文中，我们通过探索线性变换与所得数据协方差之间的关系提供协方差矩阵一个直观的几何解释。大部分教科书基于协方差矩阵的概念解释数据的形状。相反，我们采取一个反向的方法，根据数据的形状来解释协方差矩阵的概念。

在《为什么样本方差除以N-1？》的文章中，我们会讨论方差的概念，并提供了众所周知的估算样本方差公式的推导和证明。这篇文章中使用的图1表明标准差（方差的平方根）提供了数据在特征空间上传播多少的量度。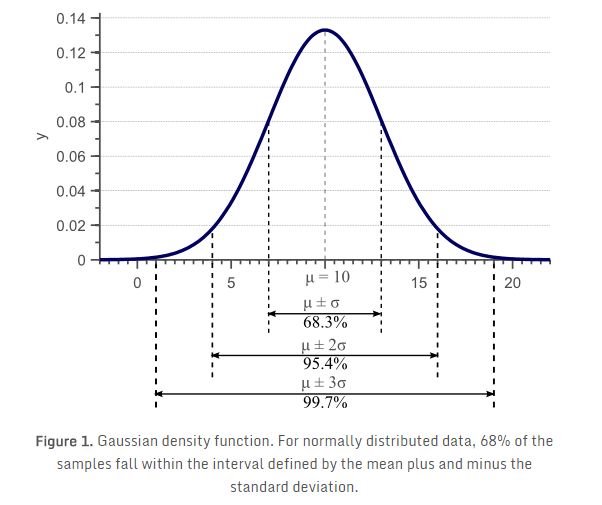 

我们发现，样本方差的无偏估计可由下式获得： 

然而，方差只能用于解释平行于特征空间轴方向的数据传播。考虑图2所示的二维特征空间：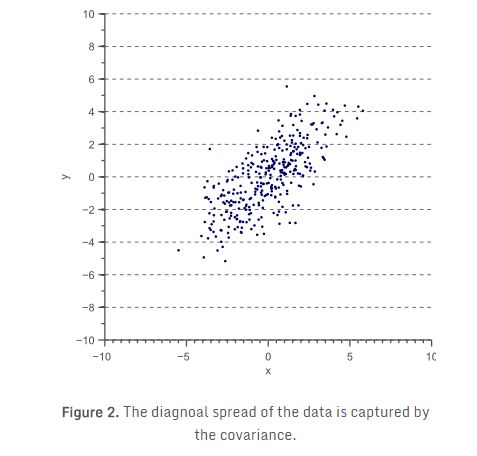 

对于这个数据，我们可以计算出在x方向上的方差和y方向上的方差。然而，数据的水平传播和垂直传播不能解释明显的对角线关系。图2清楚地显示，平均而言，如果一个数据点的x值增加，则y值也将增加，这产生了正相关。这种相关性可以通过扩展方差概念到所谓的数据“协方差”捕捉到： 

对于2D数据，我们得到，这些值可以用矩阵来表示，该矩阵叫做协方差矩阵：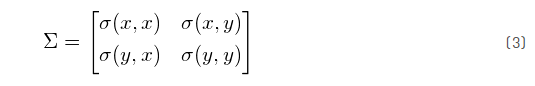 

如果x与y是正相关的，那么y和x也是正相关的。换句话说，。因此，协方差矩阵始终是一个对称矩阵，其对角线上是方差，非对角线上是协方差。二维正态分布数据由它的均值和2x2协方差矩阵就可以完全解释。同样，一个3x3协方差矩阵用于捕捉三维数据的传播，一个NxN协方差矩阵捕获N维数据的传播。

图3展示了数据的整体形状如何定义协方差矩阵： 

协方差矩阵的特征值分解

在下一节，我们将讨论协方差矩阵如何被解释为白色数据转换成我们观察到数据的线性操作。然而，在深入技术细节之前，对特征向量和特征值如何唯一地确定协方差矩阵（数据形状）有一个直观的认识是非常重要的。

正如我们在图3看到的，协方差矩阵定义了我们数据的传播（方差）和方向（协方差）。因此，如果我们想用一个向量和它的大小来表示协方差矩阵，我们应该简单地尝试找到指向数据最大传播方向上的向量，其大小等于这个方向上的传播（方差）。

如果我们定义这个向量为，那么我们数据D到这个向量上的映射为，映射数据的方差是。由于我们正在寻找指向最大方差方向的向量，所以我们应该选择它的成分，使得映射数据的协方差矩阵尽可能的大。最大化的形式为的任何函数，其中是归一化单位向量，可以用一个所谓的瑞利商表示。通过设置等于矩阵的最大特征特征向量可以获得这样瑞利商的最大值。

换句话说，协方差矩阵的最大特征向量总是指向数据最大方差的方向，并且该向量的幅度等于相应的特征值。第二大特征向量总是正交于最大特征向量，并指向第二大数据的传播方向。

现在，让我们来看看一些例子。在文章《特征值和特征向量》中http://blog.csdn.net/u010182633/article/details/45921929，我们看到一个线性变换矩阵T完全由它的特征向量和特征值定义。应用到协方差矩阵，这意味着： 
 

如果我们数据的协方差矩阵是对角矩阵，使得协方差是零，那么这意味着方差必须等于特征值λ。如图4所示，特征向量用绿色和品红色表示，特征值显然等于协方差矩阵的方差分量。 

然而，如果协方差矩阵不是对角的，使得协方差不为零，那么情况稍微更复杂一些。特征值仍代表数据最大传播方向的方差大小，协方差矩阵的方差分量仍然表示x轴和y轴方向上的方差大小。但是，因为数据不是轴对齐的，所以这些值不再与图5所示的相同。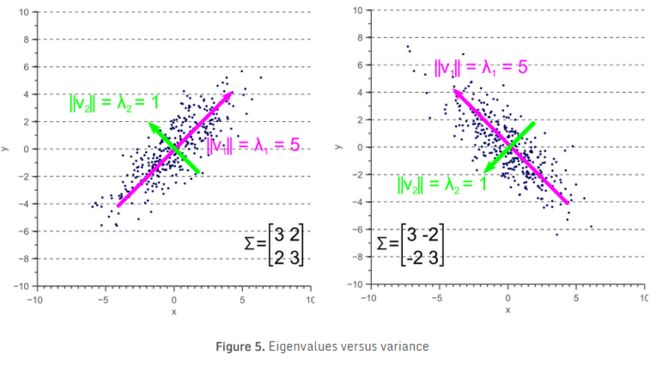 

通过比较图5与图4，可以清楚地看到特征值表示沿特征向量方向数据的方差，而协方差矩阵的方差分量表示沿轴的传播。如果没有协方差，则这两个值是相等的。

协方差矩阵作为线性变换

现在，让我们忘了协方差矩阵。图3的实例可以简单地认为是图6的一个线性变换实例：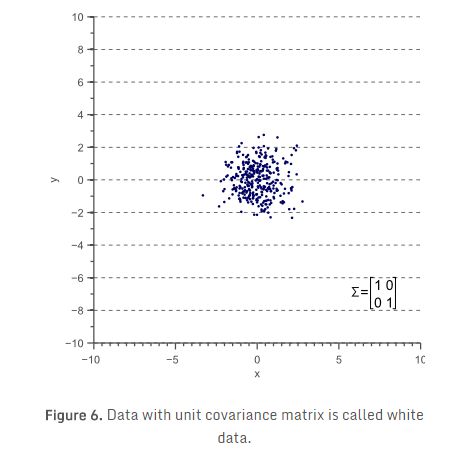 

图6所示的数据是D，则图3所示的每个实例可以通过线性变换D得到：

其中T是变换矩阵，包括一个旋转矩阵R和缩放矩阵S： 

这些矩阵定义如下： 
 
其中是旋转角度。

 
分别是x方向和y方向的比例因子。

在下面的段落中，我们将讨论协方差矩阵与线性变换矩阵T= RS之间的关系。

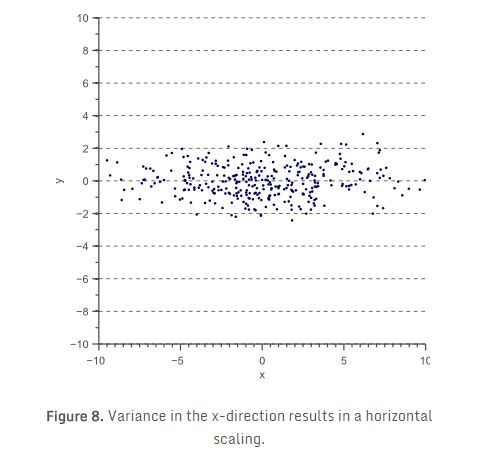
让我们先从未缩放（缩放相当于1）和未旋转的数据开始。在统计中，这往往为“白数据’，因为它的样本是从标准正态分布引出的，因此对应于白（不相关）噪声：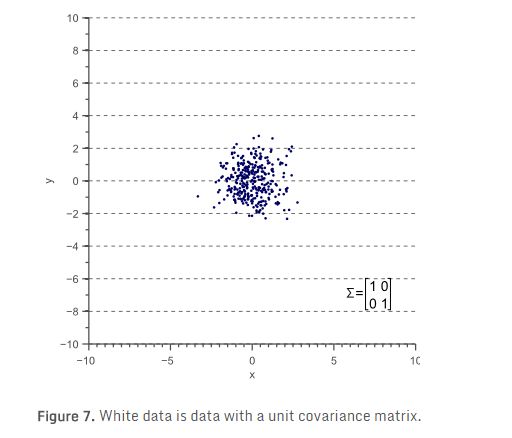 

这个“白色”数据的协方差矩阵等于单位矩阵，使得方差和标准差等于1，协方差等于零：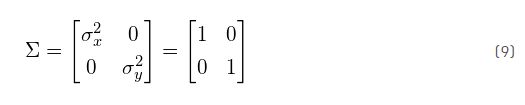 

现在让我们用因子4在x方向缩放数据： 

数据D’现在如下： 

D’的协方差现在是： 

D’的协方差与线性变换矩阵T有关系，D=TD，其中: 

然而，虽然数据在x和y方向上缩放时等式（12）成立，但是应用旋转是否依然成立呢？为了调查一般情况下线性变换矩阵T和协方差矩阵之间的关系，我们试图分解协方差矩阵为旋转和缩放矩阵的乘积。

正如我们前面所看到的，我们可以用特征向量和特征值表示协方差矩阵： 
 

等式（13）保存矩阵Σ的每个特征向量和特征值。在2D情况下，我们得到两个特征值和两个特征值。由公式（13）定义的两个等式可以有效地用矩阵符号来表示： 
 
其中V是矩阵，它的列是Σ的特征向量，L是对角矩阵，其非零元素对应特征值。

这意味着我们可以将协方差矩阵表示为特征向量和特征值的函数： 

方程（15）就是所谓协方差矩阵特征值分解，并可以使用奇异值分解算法来获得。而特征向量表示数据最大方差的方向，特征值表示那些方向方差的幅度。换言之，V表示旋转矩阵，而表示一个缩放矩阵。协方差矩阵可以进一步分解为： 
 

在等式（6）中，我们定义了一个线性变换T= RS。由于S是对角缩放矩阵，所以S=ST。此外，由于R为正交矩阵，R-1=RT。因此，协方差矩阵可以写为： 

换言之，如果我们应用由T=RS定义的线性变换到图7所示的原始白数据，我们得到了旋转和缩放的数据D’及协方差矩阵。这示于图10：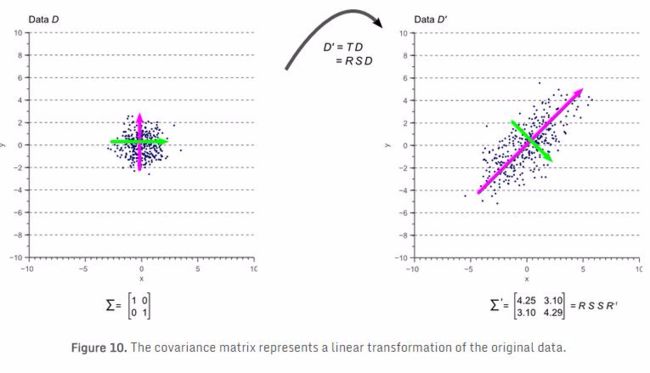 

图10的彩色箭头表示特征向量。最大特征向量，即与最大特征值对应的特征向量，总是指向数据最大方差的方向，并由此确定其方位。次特征向量总是正交于最大特征向量，因为旋转矩阵的正交性。

总结 
在本文中，我们表明观察到数据的协方差矩阵与白色不相关数据的线性变换有直接的关系。此线性变换完全由数据的特征向量和特征值确定。而特征向量表示旋转矩阵，特征值对应于每个维度上缩放因子的平方。

 

 

来源： https://www.cnblogs.com/nsnow/p/4758202.html