【c/c++】queue, priority_queue, 堆以及哈夫曼树

1.  首先对 queue 队列进行介绍，队列是一种先进先出(FIFO)的数据结构，与栈很相似，不同之处就是它每次从队首出队，而不是从队尾出队，在c++中引用 #include使用相关函数，定义方法: queue q; 用queue q2(q) 实现拷贝操作。主要的函数有push(i), pop(), front(), back(), empty(), size()与栈的基本类似, 没有 top()，front 表示队首，back表示队尾。

 先来看一下具体的使用：

#include
#include
#include
#include
#include
using namespace std;

int main()
{
	queue q;
	for (int i = 0; i < 10; i++)
		q.push(i);
	printf("执行从 0 到 9的进队操作后的q.size()为: %d\n", q.size());
	printf("q.front()为:  %d, q.back()为： %d\n",q.front(),q.back());
	queue q2(q);
	printf("queue q2(q)实现拷贝操作后的 q2.size()为: %d\n",q2.size());
	q.pop();
	printf("执行q.pop()后的q.front()为: %d, q.back()为: %d\n",q.front(), q.back());
	printf("此时q.size()为: %d\n", q.size());
	while (!q.empty())
	{
		printf("对 %d 执行出队操作\n",q.front());
		q.pop();
	}
	if (q.empty())
	{
		printf("全部出队完成，q.empty()为真，此时q.size()为: %d", q.size());
	}
	printf("\n");
	return 0;
}

运行结果：

执行从 0 到 9的进队操作后的q.size()为: 10
q.front()为:  0, q.back()为： 9
queue q2(q)实现拷贝操作后的 q2.size()为: 10
执行q.pop()后的q.front()为: 1, q.back()为: 9
此时q.size()为: 9
对 1 执行出队操作
对 2 执行出队操作
对 3 执行出队操作
对 4 执行出队操作
对 5 执行出队操作
对 6 执行出队操作
对 7 执行出队操作
对 8 执行出队操作
对 9 执行出队操作
全部出队完成，q.empty()为真，此时q.size()为: 0
请按任意键继续. . .

2.  对于priority_queue优先序列，也是在#include中实现的，它和队列一样，只能从队尾插入元素，从队首删除元素，但是不同的是，它只有top()操作，没有 front() 和 back() 操作，这一点又和栈比较类似，优先序列可以自动完成内部的排序，并且是按照堆的方式来实现的，速度很快，在 O(logn)量级找到最小或最大的值，每次pop后会自动调整为小顶堆或大顶堆，甚至可能超过快排sort。对于堆，可以理解成一种二叉树的形式，大二数据结构时学过，各种上浮之类的操作给我留下了深深的阴影，等有时间再找个时间认真复习一下，这里暂时不说了。 它的定义方式有两种，一种是一个参数 priority_queue q;  只定义了元素的类型，默认是大顶堆(堆的顶点(即二叉树的根结点)的权值是最大的，小顶堆则是最小)；还有3个参数的(3个不可少1)，priority, greater(这两个>>之间最好有个空格)> q(或者less或者自定义))，greater是小顶堆，less是大顶堆，这里与sort很像，less是默认的升序，greater是默认的降序，但理解起来又好像很不同，还可以自定义，但是不能像sort那样写一个自定义函数(小顶堆和降序的很类似)，必须定义一个结构体，见程序。最好用greater来表示小顶堆。greater在vs2015中要引用，但less则不需要。

代码:

#include
#include
#include
#include
#include
#include
using namespace std;

//greater相当于前比后大，降序操作，这里优先序列又很像是一个栈，即把小的排到栈顶
//不能靠 bool cmp(int x, int y){return x > y;}来实现
struct cmp {
	bool operator()(int x, int y)
	{
		return x > y;
	}
};

int main()
{
	priority_queue q;
	q.push(1);
	q.push(5);
	q.push(3);
	q.push(9);
	printf("按照先后顺序向priority_queue q 中 push: 1 5 3 9\n");
	while (!q.empty())
	{
		printf("此时队首 q.top()为: %d\n", q.top());
		q.pop();
	}
	printf("完成了全部出队操作，此时q.size()为: %d\n", q.size());
	//less是大顶堆，与1个参数默认是相同的，无需functional，greater是小顶堆,需要functional
	//less的队首总是最大的，sort中的less是升序的，注意区别，less总是默认的
	priority_queue, less > q2;
	q2.push(1);
	q2.push(20);
	q2.push(3);
	printf("使用, less> q2, 先后push: 1, 20, 3后q2.top()为: %d\n", q2.top());
	priority_queue, greater > q3;
	q3.push(5);
	q3.push(4);
	q3.push(7);
	printf("使用, greater > q3,先后push: 5,4,7后q3.top()为: %d\n",q3.top());
	priority_queue, cmp> q4;
	q4.push(3);
	q4.push(1);
	q4.push(5);
	printf("使用, cmp> q4(小顶堆), 先后push: 3,1,5后的q4.top()为: %d\n",q4.top());
	return 0;
}

运行结果:

按照先后顺序向priority_queue q 中 push: 1 5 3 9
此时队首 q.top()为: 9
此时队首 q.top()为: 5
此时队首 q.top()为: 3
此时队首 q.top()为: 1
完成了全部出队操作，此时q.size()为: 0
使用, less> q2, 先后push: 1, 20, 3后q2.top()为: 20
使用, greater > q3,先后push: 5,4,7后q3.top()为: 4
使用, cmp> q4(小顶堆), 先后push: 3,1,5后的q4.top()为: 1
请按任意键继续. . .

下面的这个例子比较容易理解，通过对结构体的优先级设置可以输出想要的结果，下面是价格大的优先级高，在堆的顶部：

#include
#include
#include
#include
#include
#include
using namespace std;

struct fruit{
    string name;
    int price;
    friend bool operator < (fruit f1, fruit f2){
        return f1.price < f2.price;
    }
}f1,f2,f3;

int main()
{
	priority_queue q;
	f1.name = "桃子";
	f1.price = 10;
	f2.name = "梨子";
	f2.price = 20;
	f1.name = "苹果";
	f2.price = 30;
	q.push(f1);
	q.push(f2);
	q.push(f3);
	cout << q.top().name << " " << q.top().price << endl;
	return 0;
}

运行结果：

 

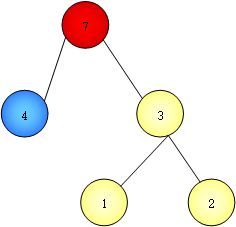
3.  接下来是哈夫曼树，还记得大二时曾经在下哈夫曼树为了省事，直接在纸上画了树，拍了照片直接传到电子文档当作业交了，举一个例子，在判断一个人的年龄时，有 10s, 20s,30s,40s,50s几种选项，一般我们写一个switch-case来判断，但是当数据极大时，效率显然是非常的低的，这实际就是一种判定树的问题，我们的哈夫曼树就是在寻找一棵判定次数最少的树，加入我们有一系列的权值，比如10s的权值是0.14,20s的权值是0.5....那么通过合理的安排这棵树的构造，我们能够大大的减少判定的次数，这里我们再来介绍路径，指的就是从根结点到目标结点需要经过几条分支数目。路径*权值为某结点的带权路径长度，只需计算叶子结点的带权路径长度，我们就是在求一棵树的所有叶子结点带权路径长度最小时的情况。很显然，当权值越大的结点越靠近根结点，则越接近哈夫曼树，在这个过程中我们可以添加非叶子结点。过程是将所有叶子结点放入集合 K 中，通过每次找最小的两个构造一父节点，将两个叶子结点的权值之和赋予父节点的权值，将父节点放入集合 K 中，删除原来的两个叶子结点，再从集合 K 中重复找2个最小的，注意不一定找的是上次生成的父节点！！！当 K 中只有1个结点时，即为根结点的权值，完成了哈夫曼树的构造，在这个过程中将哈夫曼树所有非叶子结点的权值相加，绝对不能加上叶子结点，会多计算一次得到的就是带权路径长度！！！因为中间生成的非叶子结点的权值，相当于对叶子结点经过的路径长度进行了计算：

带权路径长度理论值：1 * 2 + 2 * 2 + 4 * 1 = 10
根据所有非叶子结点的权值之和计算：7 + 3 = 10

1 和 2 被加了2次，恰为它到根结点的路径长2。

来看一个题目:

题目描述：

哈夫曼树，第一行输入一个数 n，表示叶结点的个数。需要用这些叶结点生成哈夫曼树，根据哈夫曼树的概念，这些结点有权值，即 weight，题目需要输出所有结点的值与权值的乘积之和。

输入：

输入有多组数据。

每组第一行输入一个数 n，接着输入 n 个叶节点（叶节点权值不超过 100，2<=n<=1000）。

输出：

输出权值。

样例输入：

5

1 2 2 5 9

样例输出：

37

这题就是给出叶子结点的权值，求带权路径长度，代码中假的都是非叶子结点，包括了根结点：

#include
#include
#include
#include
#include
#include
using namespace std;
//没必要使用数组
//int buf[1000];


int main()
{
	int n;
	priority_queue, greater > q;
	while (scanf("%d", &n) != EOF)
	{
		//重要，每次都要确保q是空的
		while (!q.empty())
			q.pop();
		for (int i = 0; i < n; i++)
		{
			int x;
			scanf("%d",&x);
			q.push(x);
		}
		//最终带权路径长度
		int res = 0;
		while (q.size() != 1)
		{
			int l_min = q.top();
			q.pop();
			int r_min = q.top();
			q.pop();
			int sum;
			sum = l_min + r_min;
			res += sum;
			q.push(sum);
		}
		printf("%d\n",res);


	}
	return 0;
}

 运行结果:

5
1 2 2 5 9
37
(下面是上图例子所给出的结果)
3
4 1 2
10