文章来自微信公众号【机器学习炼丹术】。我是炼丹兄,有什么问题都可以来找我交流,近期建立了微信交流群,也在朋友圈抽奖赠书十多本了。我的微信是cyx645016617,欢迎各位朋友。
参考目录:
@
目录
- 1 网络结构
- 2 参数量分析
- 3 PyTorch实现与解析
上一节课讲解了MobileNet的一个DSC深度可分离卷积的概念,希望大家可以在实际的任务中使用这种方法,现在再来介绍EfficientNet的另外一个基础知识—, Squeeze-and-Excitation Networks压缩-激活网络
1 网络结构
可以看出来,左边的图是一个典型的Resnet的结构,Resnet这个残差结构特征图求和而不是通道拼接,这一点可以注意一下
这个SENet结构式融合在残差网络上的,我来分析一下上图右边的结构:
- 输出特征图假设shape是\(W \times H \times C\)的;
- 一般的Resnet就是这个特征图经过残差网络的基本组块,得到了输出特征图,然后输入特征图和输入特征图通过残差结构连在一起(通过加和的方式连在一起);
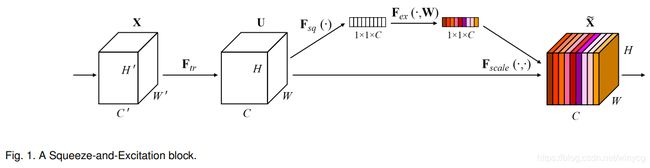
- SE模块就是输出特征图先经过一个全局池化层,shape从\(W \times H \times C\)变成了\(1 \times 1 \times C\),这个就变成了一个全连接层的输入啦
-
压缩Squeeze:先放到第一个全连接层里面,输入\(C\)个元素,输出\(\frac{C}{r}\),r是一个事先设置的参数;
-
激活Excitation:在接上一个全连接层,输入是\(\frac{C}{r}\)个神经元,输出是\(C\)个元素,实现激活的过程;
-
- 现在我们有了一个\(C\)个元素的经过了两层全连接层的输出,这个C个元素,刚好表示的是原来输出特征图\(W \times H \times C\)中C个通道的一个权重值,所以我们让C个通道上的像素值分别乘上全连接的C个输出,这个步骤在图中称为Scale。而这个调整过特征图每一个通道权重的特征图是SE-Resnet的输出特征图,之后再考虑残差接连的步骤。
2 参数量分析
每一个卷积层都增加了额外的两个全连接层,不够好在全连接层的参数非常小,所以直观来看应该整体不会增加很多的计算量。 Resnet50的参数量为25M的大小,增加了SE模块,增加了2.5M的参数量,所以大概增加了10%左右,而且这2.5M的参数主要集中在final stage的se模块,因为在最后一个卷积模块中,特征图拥有最大的通道数,所以这个final stage的参数量占据了增加的2.5M参数的96%。
3 PyTorch实现与解析
先上完整版的代码,大家可以复制本地IDE跑一跑,如果代码有什么问题可以联系我:
import torch
import torch.nn as nn
import torch.nn.functional as F
class PreActBlock(nn.Module):
def __init__(self, in_planes, planes, stride=1):
super(PreActBlock, self).__init__()
self.bn1 = nn.BatchNorm2d(in_planes)
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
if stride != 1 or in_planes != planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, planes, kernel_size=1, stride=stride, bias=False)
)
# SE layers
self.fc1 = nn.Conv2d(planes, planes//16, kernel_size=1)
self.fc2 = nn.Conv2d(planes//16, planes, kernel_size=1)
def forward(self, x):
out = F.relu(self.bn1(x))
shortcut = self.shortcut(out) if hasattr(self, 'shortcut') else x
out = self.conv1(out)
out = self.conv2(F.relu(self.bn2(out)))
# Squeeze
w = F.avg_pool2d(out, out.size(2))
w = F.relu(self.fc1(w))
w = F.sigmoid(self.fc2(w))
# Excitation
out = out * w
out += shortcut
return out
class SENet(nn.Module):
def __init__(self, block, num_blocks, num_classes=10):
super(SENet, self).__init__()
self.in_planes = 64
self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)
self.linear = nn.Linear(512, num_classes)
def _make_layer(self, block, planes, num_blocks, stride):
strides = [stride] + [1]*(num_blocks-1)
layers = []
for stride in strides:
layers.append(block(self.in_planes, planes, stride))
self.in_planes = planes
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = F.avg_pool2d(out, 4)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
def SENet18():
return SENet(PreActBlock, [2,2,2,2])
net = SENet18()
y = net(torch.randn(1,3,32,32))
print(y.size())
print(net)