Part -1: 参考资料
参考资料1
万分感谢这个大佬,祝他报送清华北大!
本文同步发表于知乎
Part 0: 一些介绍
莫队由莫涛神仙首次提出,是一种区间操作算法。
即便是板子题,难度也很高(差评)
所以,在阅读后文之前,请你先深呼吸,喝杯咖啡,吃点饼干,听听自己喜欢的歌
然后,停止呼吸,放下杯子,扔开饼干,摘下耳机,接受莫涛大神思想光辉的洗礼
Part 1:莫队算法的引入
先别谈莫队,我们来回顾一下,遇到区间问题一般怎么解决?
很好,暴力线段树
也就是说,我们一直在通过维护两个序列——左序列\([l,mid]\)与右序列\([mid + 1,r]\),从而来维护\([l, r]\),当然,这个操作会一直递归下去
然而,当题目这么问:
令数组\(Q\)大小为\(n\)且每个元素\(Q_i < n\),有\(m\)个询问,每次询问给定\(l,r\),请找出\([l,r]\)中至少重复出现\(k\)此的数字的个数
换句话说:
在\(Q_l\)到\(Q_r\)内找出现次数多余\(k\)的数字的个数
of course,你可以暴力,但你会暴零
那么我们试着用线段树,首先,你需要维护左边的序列,然后你需要维护右边的序列,然后……
然后你会发现很难做到短时间甚至\(O(1)\)的时间完成对线段树单一节点的维护,因为你总是要层层递进向上叠加。
淦!这不是欺负人吗
我们先试试暴力吧,用个\(count\)记录一下出现次数,然后在扫一遍
暴力是万能的,答案当然正确,但是你的时间复杂度哭了——\(O(n^2)\)
那么我们可以看看是否可以改进一下,用上\(t(wo)p(oints)\)算法:
假设有两个指针,\(l\)和\(r\),每次询问的时候用移动\(l\)和\(r\)的方式来尝试和要求区间重合
是不是有点蒙?我举个栗子
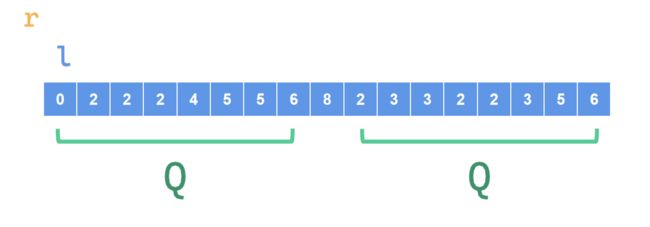
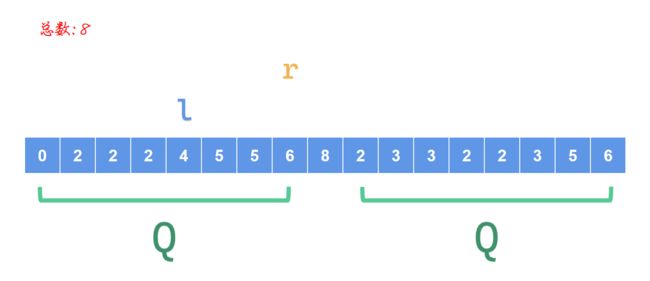
此图中,两个Q是待求的区间
初始化\(r = 0,l = 1\)
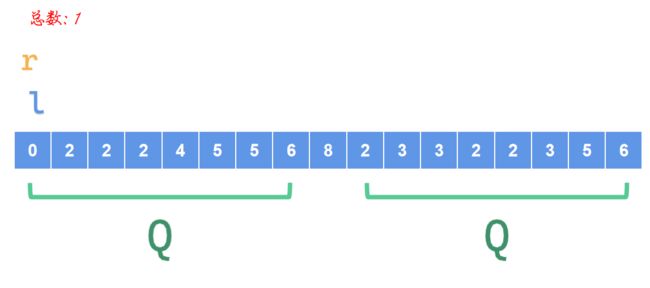
此时,发现\(l\)和要求的区间左端重合了,而\(r\)没有,那么我们把\(r\)往右边移动一位
此时,\(r\)发现了一个新的值\(0\),总数记录一下,继续右移动
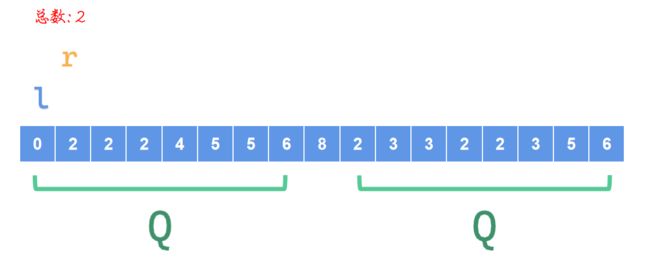
\(r\)又发现了一个新数值\(2\),总数记录一下,继续右移动
此处\(2\)被记录过了,总数值不变
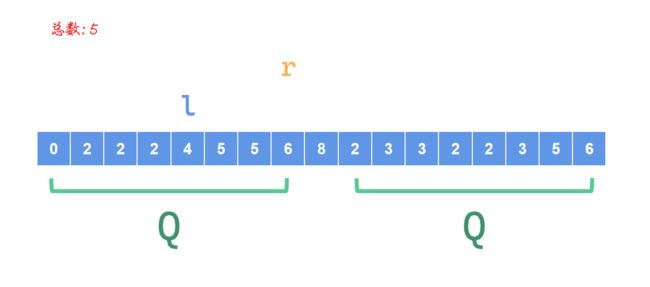
一直到\(r\)与右端点重合,得到下图:
第一个区间就算处理完了,我们来看下一个
首先,\(l\)不在左端点,我们把它右移
这一次,\(l\)所遇到的数值在区间\([l, r]\)只能够存在,总数不变
下一次也是如此,一直到
你会发现,这时,区间\([l,r]\)将(也就是在下一次移动后)不会有\(2\)存在了,那么总数就一个\(-1\),而正好本题需要统计的就是区间内数值的个数,总数改变:
如此循环往复,得到最终答案,所以我们可以得出这个代码
int arr[maxn], cnt[maxn] // 每个位置的数值、每个数值的计数器
int l = 1, r = 0, now = 0; // 左指针、右指针、当前统计结果(总数)
void add(int pos) { // 添加一个数
if(!cnt[arr[pos]]) ++ now; // 在区间中新出现,总数要+1
++ cnt[arr[pos]];
}
void del(int pos) { // 删除一个数
-- cnt[arr[pos]];
if(!cnt[arr[pos]]) -- now; // 在区间中不再出现,总数要-1
}
void work() {
for(int i = 1; i <= q; i ++) {
int ql, qr;
scanf("%d%d", &ql, &qr);
while(l < ql) del(l++); // 左指针在查询区间左方,左指针向右移直到与查询区间左端点重合
while(l > ql) add(--l); // 左指针在查询区间左端点右方,左指针左移
while(r < qr) add(++r); // 右指针在查询区间右端点左方,右指针右移
while(r > qr) del(r--); // 否则左移
printf("%d\n", now); // 输出统计结果
}
}
嗯,干得漂亮,但是这是莫队吗?不是
如果区间特别多,\(l,r\)反复横跳,结果皮断了腿,时间复杂度\(O(nm)\)
那么现在的问题已经变成了:如何尽量减少\(l,r\)移动的次数?
Part 2:莫队的正确打开方式
首先,看到尽量减少\(l,r\)移动的次数,我们会想到排个序
排序排什么的顺序呢?是排端点吗?显然不是,哪怕左端点有序,右端点就会杂乱无章;右端点有序,左端点就会杂乱无章……
这里,我们运用一下分块的思想,把序列分为\(\sqrt{n}\)块,把查询区间按照左端点所在块的序号排个序,如果左端点所在块相同,再按右端点排序。
这个算法需要的时间复杂度为\(sort+move_{\texttt{左指针}}\)
由于\(sort\)的时间复杂度为\(O(n\log n)\),\(move_{\texttt{做指针}}\)的时间复杂度为\(O(n\sqrt{n})\),那么总的时间复杂度为\(O(n\sqrt{n})\)
好耶!降了一个根号!鼓掌!
其次,我们需要考虑一下更新的策略
一般来说,我们只要找到指针移动一位以后,统计数据与当前数据的差值,找出规律(可以用数学方法或打表),然后每次移动时用这个规律更新就行
最后给出总代码:
#include
#include
#include
#include
using namespace std;
#define maxn 1010000
#define maxb 1010
int aa[maxn], cnt[maxn], belong[maxn];
int n, m, size, bnum, now, ans[maxn];
struct query {
int l, r, id;
} q[maxn];
int cmp(query a, query b) {
return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
#define isdigit(x) ((x) >= '0' && (x) <= '9')
int read() {
int res = 0;
char c = getchar();
while(!isdigit(c)) c = getchar();
while(isdigit(c)) res = (res << 1) + (res << 3) + c - 48, c = getchar();
return res;
}
void printi(int x) {
if(x / 10) printi(x / 10);
putchar(x % 10 + '0');
}
int main() {
scanf("%d", &n);
size = sqrt(n);
bnum = ceil((double)n / size);
for(int i = 1; i <= bnum; ++i)
for(int j = (i - 1) * size + 1; j <= i * size; ++j) {
belong[j] = i;
}
for(int i = 1; i <= n; ++i) aa[i] = read();
m = read();
for(int i = 1; i <= m; ++i) {
q[i].l = read(), q[i].r = read();
q[i].id = i;
}
sort(q + 1, q + m + 1, cmp);
int l = 1, r = 0;
for(int i = 1; i <= m; ++i) {
int ql = q[i].l, qr = q[i].r;
while(l < ql) now -= !--cnt[aa[l++]];
while(l > ql) now += !cnt[aa[--l]]++;
while(r < qr) now += !cnt[aa[++r]]++;
while(r > qr) now -= !--cnt[aa[r--]];
ans[q[i].id] = now;
}
for(int i = 1; i <= m; ++i) printi(ans[i]),putchar('\n');
return 0;
}
Part 3:关于莫队的一些卡常数
卡常数作为OIer的家常便饭,相信大家一定不陌生了
卡常数包括:
- 位运算
O2- 快读
- ……
而莫队的神奇之处在于他的独特优化:奇偶性排序
原代码:
int cmp(query a, query b) {
return belong[a.l] == belong[b.l] ? a.r < b.r : belong[a.l] < belong[b.l];
}
改为
int cmp(query a, query b) {
return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
别人说跑的很快我还不信,自己跑了一下才知道……
真的跑的很快啊……
Part 4: 能修改的莫队
我知道,你拿着上面别个大佬写的代码(再次膜拜写这个代码的大佬orz)兴冲冲的去刷题,一路上披荆斩棘,直到你看到了Luogu1903——国家集训队-数颜色,你彻底傻了眼
妈耶,他要是这么一修改我岂不是要重新sort?跑了跑了
由于莫队本身就是离线的,而你需要修改,得想个办法让他在线,具体做法是:“就是再弄一指针,在修改操作上跳来跳去,如果当前修改多了就改回来,改少了就改过去,直到次数恰当为止。”
(再次感谢这个大佬,,好喜欢这个解释)