孪生网络:使用双头神经网络进行元学习
深度神经网络有一个大问题-他们一直渴望数据。 当数据太少时(无法到达算法可以接受的数量)深度神经网络很难推广。 这种现象突出了人类和机器认知之间的差距。 人们可以通过很少的训练示例来学习复杂的模式(尽管速度较慢)。
需要像我们这样思考的机器
自我监督学习的研究正在发展,以开发完全不需要标签的结构(在训练数据本身中巧妙地找到标签),但其用例却受到限制。
半监督学习是另一个快速发展的领域,它利用通过无监督培训学到的潜在变量来提高监督学习的性能。这是一个重要的概念,但其范围仅限于无监督与受监督数据比率相对较大且无标记数据与标记数据兼容的用例。
也许一个主意囊括了所有主意-开发能够充分利用有限的标记数据的方法和体系结构;使机器更像人类那样思考。正式名称是元学习,通常称为“学习如何学习”。
元学习和自然语言处理中常用的术语是“少次学习”或“零次学习”。这些指的是能够用很少或没有(分别)预先训练模型的数据来识别新概念。零次学习的一个例子是在接受英语到法语和法语到德语翻译任务的培训后将英语翻译成德语。
孪生网络(Siamese network)
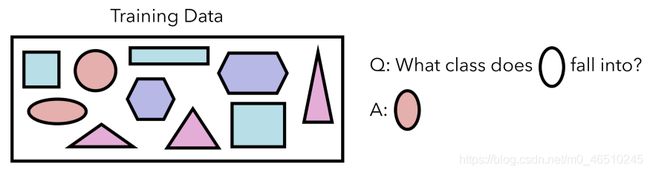
让我们看一下一项需要少量学习的机器学习任务,以及孪生网络的独特架构是如何实现的。 我们的训练数据包含十个形状,属于四种形状类型之一。 每个类别的数据量很少,但我们希望能够归纳和识别新形状。
我们的数据集有10个形状。
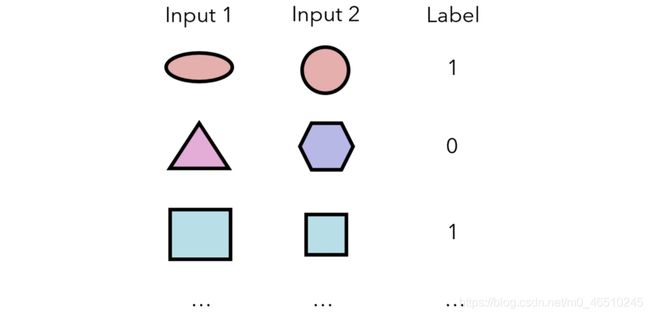
孪生神经网络测量两个输入属于同一类别的概率。 从这个意义上讲,它不会直接输出任何输入的类; 相反,它基于对一个输入的理解与另一个输入的显式关系。 将产生以下数据来训练模型:
因此,对于数据集中的n个样本,可以在(n²-n)/ 2个唯一的输入对(每个输入之间有n²个可能的配对,两个相同样本之间的n个配对,/ 2以考虑a&b和n)上训练孪生网络。 b&a被视为单独的组合)。
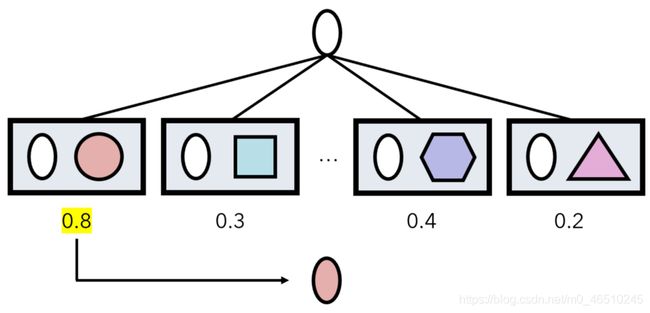
然后,在预测某些输入a的过程中,孪生网络对(a,x)进行数据集中每个样本x的预测。 a的类别是产生最大网络输出的数据点x的类别。
方框代表通过算法的预测,数字代表输出。
孪生网络采用两个输入,然后通过嵌入函数将它们(分别)编码为特征向量,该函数由几个卷积层组成。 两个特征向量通过“距离层”合并,该距离层仅计算L1距离| f1-f2 |。 或者,也可以通过L2,余弦等计算距离。输出是距离矢量的S型压缩线性组合。
值得一提的是,在这种情况下,“嵌入”实际上只是原始输入层与卷积神经网络的传统元素(如卷积层和池化层)的编码表示。嵌入的原因是,嵌入点之间的距离被获取并处理以形成输出
*注:嵌入定义为一个空间,在该空间中映射点之间的距离意味着某些东西;例如,在NLP嵌入中,单词“ man”和“ boy”在空间中的物理距离应比“ man”和“ purple”的关系小,例如,它们之间的关系很小。
孪生网络的名称来自于连体双胞胎,或双胞胎在出生时相连的双胞胎,看起来好像有两个头。考虑到孪生网络的出现,这是有道理的。
孪生网络的一个关键部分是,虽然有两个编码两个输入的“头部”,但它们具有相同的权重。这很有道理; f(a,b)应具有与f(b,a)相同的内部构成。无论输入的顺序如何,编码过程都必须相同。
可以说孪生网络在图像识别过程中增加了更多的结构。卷积神经网络更不用担心:“这是一个庞大的架构,您可以用它来做您想做的事”;连体网络将图像映射到嵌入(确定图像中的关键特征),通过该嵌入计算距离(直接比较两者)并进行解释以得出结果。
孪生网络背后的思想
从根本上讲,孪生网络代表了我们对图像识别的看法的转变。 当机器对彼此相关的概念进行理解时(与传统的图像识别一样,从零开始构建表示形式则相反),他们可以学习的数据更少。
这很好地解释了为什么人们能够通过很少的训练实例就能识别和学习概念。 我们通过复杂的层次结构和相互纠缠的关系来存储信息:橙色类似于苹果,但与汽车有很大不同。 当与现有概念相关地描述一个新概念时,学习会更有效。
作为另一个类推,请考虑以下数字系列:2101、2102、2099、2101、2097、2100、2095。继续-尝试记住它,然后再向下滚动。 它很难!
幸运的是,有一种更有效的方式来记忆该集合:表达与前一个数字相关的每个数字。 如果我们记得第一个数字是2101,我们只需要记住1,-3、2,-4、3,-5。 与其处理复杂的大型概念(相对于数量级而言),不如将它们相对于其他对象建立起来,会更加有效。
实际应用与讨论
孪生网络可用于一次性学习-通过数据增强仅学习一个训练示例即可学习概念。 例如,可以对图像进行较小的旋转,移动和缩放。 由于数据集的大小以n²的速度增长,因此可以提供大量信息。
此外,它们还可以用于验证问题(识别同一个人的两个面孔,两个指纹,两个手势等)—实际上,许多最新的实时面部识别系统都采用了孪生神经网络。 这些网络在执行此任务方面优于标准图像识别体系结构,后者在处理大量分类时遇到了巨大困难(我们正在与成千上万的人交谈)。
通常,孪生网络可以很好地处理类不平衡问题。这使其吸引了诸如图像识别之类的任务。部分原因可以归因于嵌入的结构性;另一方面,在庞大的卷积网络的广阔区域中,微小的的特征往往被过滤掉了。
通常,答案是简单地使卷积神经网络变大,但是网络的持续超大型化已成为现实的极限。
重要的是要意识到,尽管预测过程可能很长(遍历数据中的每个样本),但实际上孪生网络是在小型数据集上进行训练的,而孪生网络通常需要较小的体系结构,同时还要加深理解。另外,实际上,项的嵌入通常是预先计算和缓存的,因为它们的值经常使用。
它们还可以用于排名问题,在该问题中,网络输出的不是两个输入是否属于同一类,而是输出第一个输入是否排名高于第二个输入,以及相似性问题(例如测量两个摘录的内容) 。
此外,孪生网络可以适用于任何数据类型,包括图像之外的那些文本和结构化数据。
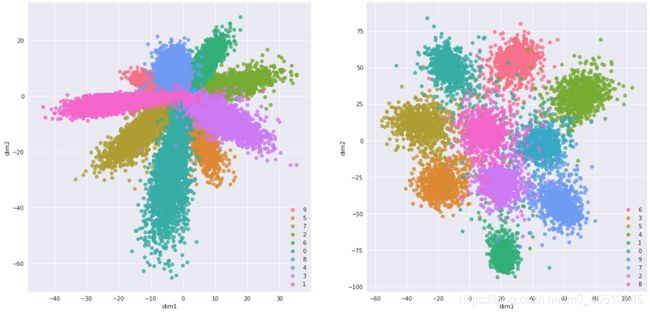
还需要注意的是,孪生网络会产生非常非常好的嵌入。与其他成熟的流形学习方法(例如t-SNE和IsoMap)相比,它们的生产成本更高,但是是很好的辅助结果。这可能是其独特架构的结果。
总结
- 当前的深度学习解决方案需要太多数据。 像自我监督和半监督学习这样的努力可以充当辅助,但是更深层的问题是机器的思维方式不像人类。 元学习旨在让AI学习学习。
- 孪生网络采用两个输入,使用与嵌入相同的权重对其进行编码,解释嵌入的差异,并输出两个输入属于同一类的概率。
- 孪生网络能够更有效地学习,因为它们在先前的学习中立足于新概念,而不是盲目地从头开始学习每一个新概念。 这就是为什么常规大小的神经网络无法执行具有大量类的任务的原因。
- 孪生网络的一些优势包括良好的泛化能力,每个类别只有一个数据点,以及对类别不平衡的强大鲁棒性。
孪生网络论文:http://www.cs.toronto.edu/~rsalakhu/papers/oneshot1.pdf
作者:Andre Ye
deephub翻译组