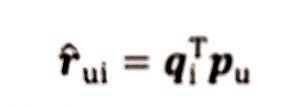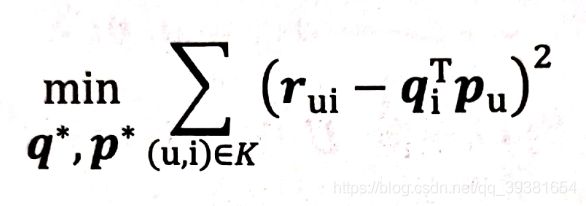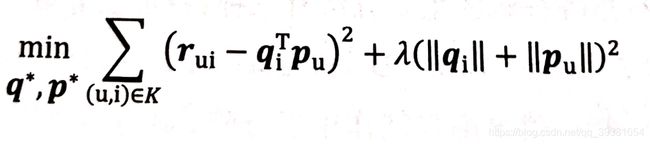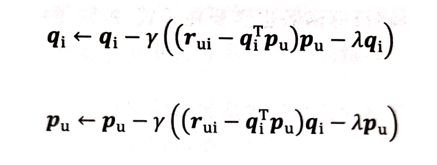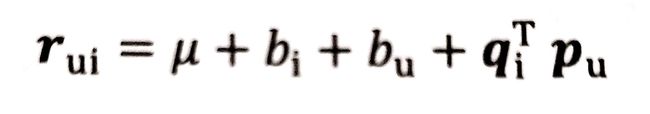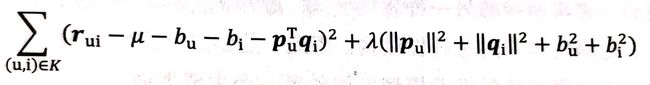【概念解析】全面理解矩阵分解MF在推荐系统中的应用
全面理解矩阵分解MF在推荐系统中的应用
那么，这是本系列的第二篇文章，讨论的是关于第一篇协同过滤之后的改进算法矩阵分解（MF），我会从多个方面讨论该算法的与案例以及它的优缺点。矩阵分解并不是某一种单一的方法，虽然我们最常用的是其中的梯度下降法，但是你会发现在我们之前学习的线性代数中有很多技术可以拿来实现矩阵分解，比如特征值分解ED和奇异值分解SVD，只不过这两种方法都有自己的不足而无法满足实际推荐系统的需要，我会在下文中说明为什么历史选择了梯度下降法。其实，我发现我在上一节最后一部分给出的案例代码当中写的其实不是单纯的协同过滤系统，而是结合了SVD奇异值分解去分解协同过滤共现矩阵的改进版协同过滤，大家可以结合来看看，案例本身是模仿自《机器学习实战》这本书。不过，我们主要还是针对在推荐系统中的应用来去解释MF的主流方法为主。
问题引入
在很多情况下，数据中的一小段携带了数据集中的大部分信息，而其他信息要么是噪声，要不就是不相关的一些信息。所以我们把目光头像了矩阵分解领域，在线性代数中还有很多矩阵分解技术。矩阵分解可以将原始矩阵表示成新的易于处理的形式，这种新的形式将是两个或多个矩阵的乘积的形式。我们可以用代数中的因子分解来类比理解这个概念，比如我想分解数字12，那么（2,6）（3,4）（1,12）都是可以接受的答案。我这里只是想说MF其实有多种方法，但是不同的矩阵分解技术具有不同的性质，其中有些更适合于某个应用，有些则更适合其他应用。
我们在上一篇文章中介绍了协同过滤的不足，协同过滤的头部效应明显、泛化能力差，矩阵分解就是针对解决这个问题而被提出的。矩阵分解简单来说就是在协同过滤算法中的共现矩阵的基础上加入了隐向量的概念，加强了模型处理稀疏矩阵的能力。针对性的解决了协同过滤存在的主要问题。
理解矩阵分解的原理
现在我们举一个例子来帮助我们理解MF的原理，就以视频网站的推荐场景来作为案例，我们可以通过使用协同过滤和使用矩阵分解两种方法来进行推荐，通过这个过程感受MF的原理。
首先我们知道其实协同过滤的逻辑非常简单，算法找到用户可能喜欢的视频是基于用户观看历史的，找到跟目标用户看过相同视频的相似用户，然后找到这些相似用户喜欢看的其他视频推荐给目标用户。
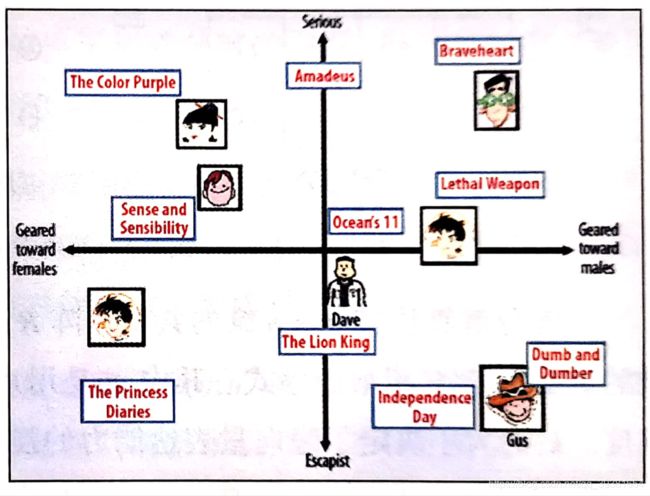
而矩阵分解算法则期望为每一个用户和视频生成一个隐向量，将用户和视频定位到隐向量的标识空间上，距离相近的用户和视频表明兴趣特点接近，在推荐过程中应该讲距离相近的视频推荐给目标用户。举个例子：
Pic_1：MF矩阵分解小例子
如果希望给图中坐标原点出的Dave推荐视频，那么可以发现离Dave最近的两个视频分别是《The Lion King》和《Ocean’s 11》那么可以根据向量距离由近及远的生成推荐列表。
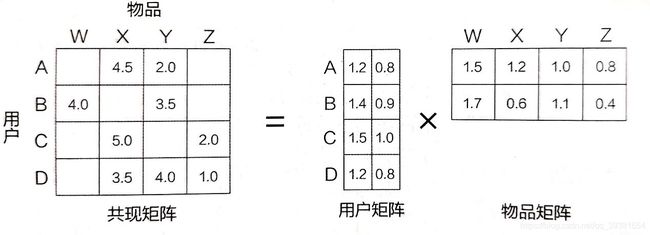
用隐向量去表达用户和物品，还要保证相似的用户及用户可能喜欢的物品的距离相近，实用的方法就是MF。在MF的框架中，用户和物品的隐向量是通过分解共现矩阵得到的：
Pic_2：矩阵分解具体样式
矩阵分解算法将m*n维的共现矩阵R分解为m*k维的用户矩阵U和k*n维的物品矩阵V相乘的形式。其中m为用户的数量，n为物品的数量，k是隐向量维度。K的大小决定了隐向量表达能力的强弱。k的取值越小，隐向量包含的信息就越少，相对来讲泛化能力就越高；反之k取值越大，隐向量的表达能力越强，但泛化能力相对降低。但并不是说刻意为了追求高的泛化能力而去降低k的维度，这是没有意义的，因为那样推荐效果也会下降。通常k的取值是在实验的过程中折中取值的，以此来保证推荐效果和工程开销能保持平衡。
既然我们现在已经实现了分解，那么该如何计算得分rui呢（用户u对物品i的预估评分），公式如下：
For_1：MF算法得分预测函数
其中pu是用户u在用户矩阵U中对应行向量，qi是物品i对应物品矩阵中的列向量。
矩阵求解的方法分类
矩阵求解的方法常见的方法有三种：特征值分解，奇异值分解和梯度下降方法。
根据之前的学习我们知道，特征值分解只能针对方阵来进行，但是我们的实际推荐系统中的共现矩阵用户的数量往往远远大于物品的数量，所以几乎不可能出现方阵，所以显然我们不能选择特征值分解的方法来分解矩阵。
而奇异值分解相对来说就可以解决了，而且我们在机器学习阶段也学习过还比较熟悉。SVD的核心是将任意矩阵表示为三个矩阵相乘的形式，即M=UΣVT，其中，U和V分别是两个m阶和n阶的正交阵，Σ则是一个m*n的近似对角阵（因为不是方阵）。对角阵的元素值即包含着原始共现矩阵特征的隐特征。截断奇异值分解可以取Σ近似对角阵的前k个隐特征（认为前K个奇异值包含9成以上的信息），抛弃其他维度的特征来完成分解。可以说奇异值分解几乎完美的实现了我们刚刚解释的MF的原理，事实上，SVD也有着它的缺陷，最致命的两个缺陷直接导致SVD也不是适合应用到推荐系统中来的MF方法：
- 奇异值分解对于稠密的共现矩阵分解结果是很好的。但是现实是，大部分需要用到推荐的场景中，用户-物品共现矩阵的密度是很稀疏的，这与奇异值分解的应用条件相悖。如果想要应用奇异值分解就必须对缺失的元素进行填充，这也无疑加大了工作量。
- SVD的计算复杂度是非常高的，它的计算复杂度能够达到O(m*n²)的水平，这对于商品数量动辄上百万，用户千万级的系统来说是无法容忍的。
所以根据以上两个问题，SVD也不适用于大规模的系数矩阵分解问题，小规模的像我们上一节使用的数据集规模还是可以的。因此，梯度下降法成了MF的主要方法，这里对其进行主要介绍（但也是基于实际场景进行阐述的）。
梯度下降法的优化过程
我们刚才在讲述MF原理的时候给出了它的得分函数rui的表达式，所以现在我们可以去定义一个新的目标函数形式出来用于优化：
For_2：目标函数原始形式
该目标函数的目的是为了让原始评分rui与用户向量和物品向量之积qiTpu的差尽量小，这样才能最大限度的保留共现矩阵的有效信息。其中K代表的是所有用户评分样本的集合，也就是共现矩阵的全部。
但是我们根据以前的优化经验就知道，这个形式的目标函数是会发生过拟合的，他缺少正则化项的参与。（在这里简单说明一下：对于加入了正则化的损失函数来说，模型权重的值越大，损失函数越大。但是梯度下降的方向是朝着Loss小的方向发展的，因此正则化项的实际作用是希望在尽量不影响原模型与数据集之间损失表达的前提下，使模型的权重变小，权重的减小自然会让模型的输出波动更小，即降低了过拟合的发生可能。而拟合效果越好，模型的泛化能力越强，这也是优化的主要目标之一。）所以，现在为刚才我们的定义好的目标函数加上正则化项：
标题For_3：加入正则化项后的目标损失函数
然后我们后续的工作就是使用我们的老朋友，梯度下降法对目标损失函数进行迭代优化，直到目标函数收敛为止。而梯度下降的核心实际就是求偏导数，来取得梯度下降的方向和幅度。
利用求偏导的结果沿梯度的反方向对参数进行更新：（γ是学习率）
For_4：逆梯度（梯度下降）方向更新参数
迭代上述步骤不断更新参数，知道迭代次数超过设置上限或者损失函数收敛为止。
优化结果分析
在完成矩阵分解之后，既可以得到所有用户和物品的隐向量，在对某用户进行推荐时，可利用该用户的隐向量与所有物品的隐向量进行逐一的内积运算来计算出该用户对所有物品的评分预测，根据评分的高低排序取得TopN推荐序列。
可以看出在矩阵分析算法中，由于隐向量的存在，使得任意用户和物品之间都可以预测分值。而通过刚才的过程也可以知道，矩阵分解产生隐向量的过程其实就是对协同过滤共现矩阵的全局拟合过程。因此隐向量是可以囊括全局信息的，却有着更强大的泛化能力。
而对于协同过滤来说，如果两个用户没有相同的历史行为，两个物品没有共同的人购买，那么这两个用户和两个物品的相似度就都为0。因此，协同过滤CF不具备泛化利用全局信息的能力，他只能通过利用用户和物品自己的信息进行相似度计算。
方法改进（消除用户和物品打分的偏差）
在《深度学习推荐系统》中还有一种对MF的改进方案，事实上我在之前的学习中也没有关注到这一点，那就是，我们在进行矩阵分解的过程中，用户事实上是有着不同的打分体系的（比如：在5分为满分的情况下，有的用户认为3分就是很低的分数了，而有的用户认为1分才是差评）。同理，不同的物品衡量标准也有所不同（电资产评的平均分he日用品的平均分显然差异会很大）。那么我们如何应对这种问题呢（这里要学习思想，因为这个问题不仅MF会需要处理，任何时候我们都要更多地去考虑用户的心理才能开发出好的系统）
为了消除用户和物品打分偏差bias，我们通常做法是在矩阵分解时加入用户和物品的偏差向量，这个偏差可以包含一些均值信息，比如我们刚才总结的打分函数，现在就可以变化一下：
For_5：更新后的打分函数
其中，μ是全局偏差常熟，bi是物品偏差系数（可使用物品i收到的所有评分的均值来表达）同理，bu是用户偏差系数（可使用用户u给出的所有评分的均值）
当然，这样一来损失函数也要变化了：
For_6：更新后的损失函数
加入了打分偏差项之后，MF得到的隐向量就能更好地反映不同用户对不同产品的真实态度差异，事实上就是综合了更多的全局均值因素，去减少因为差异所带来的噪声。这样可以更好的去捕捉和评价数据中有价值的信息，避免推荐结果产生偏差。
矩阵分解的优势和局限性
这里讨论优势的话肯定是针对CF来说的，毕竟MF的产生就是为了解决CF的缺陷：
- 首先，泛化能力相对于CF大大增强。MF在一定程度上解决了数据稀疏的问题。
- 其次，空间复杂度相对要低，因为通过分解，我们得到了隐向量的概念表示，因此CF中需要维护的巨大的相似性矩阵可以舍弃掉了，空间复杂度大大降低。
- 最后，MF有着更好的可扩展性和灵活性。矩阵分解自重产出的是User-Item隐向量，这其实与深度学习中的Embedding思想类似，因此矩阵分解的结果非常适合与其他特征进行组合拼接，并且便于深度学习网络的结合。
关于局限性，也很明显，MF同样不容易考虑用户物品以及上下文的信息，这使得矩阵分解丧失了利用很多有效信息的机会。同时在缺乏用户历史行为时，无法进行有效推荐（尽管，在这一点上比CF要好很多）。
为了解决这些问题，逻辑回归模型以及后续发展出来的FM，FMM凭借其天然的融合不同特征的能力，主键在推荐系统领域得到更广泛的应用。关于这些模型，将在稍后的文章中继续介绍。
延伸阅读
文章撰写的过程中参考了一下前辈的博客给出了很多MF的延伸研究，有兴趣的话可以研究一下这几篇论文：（参考自 - https://blog.csdn.net/qq_23968185/article/details/70477613）
一、基于投影梯度法的非负矩阵分解
论文：Projected gradient methods for non-negative matrix factorization
代码：Matlab及Python源码
二、基于类牛顿法的最小二乘矩阵近似解法
论文：Fast Newton-type Methods for the Least Squares Nonnegative Matrix Approximation Problem
PPT：https://www.niss.org/sites/default/files/Dhillon_workshop.pdf
三、基于alternating nonnegative least squares（ANLS）框架的一种NMF分解方法
论文：Toward Faster Nonnegative Matrix Factorization: A New Algorithm and Comparisons
四、 active-set-like算法求解NMF
论文： Fast nonnegative matrix factorization: An active-set-like method and comparisons