java 从零开始手写 redis（11）clock时钟淘汰算法详解及实现

前言

java从零手写实现redis（一）如何实现固定大小的缓存？

java从零手写实现redis（三）redis expire 过期原理

java从零手写实现redis（三）内存数据如何重启不丢失？

java从零手写实现redis（四）添加监听器

java从零手写实现redis（五）过期策略的另一种实现思路

java从零手写实现redis（六）AOF 持久化原理详解及实现

java从零开始手写 redis（七）LRU 缓存淘汰策略详解

前面我们实现了 FIFO/LRU/LFU 等常见的淘汰策略，不过在操作系统中，实际上使用的是时钟页面置换算法。

LRU 的性能确实很好，不过比较消耗内存，而且实现比较麻烦。

时钟页面置换算法就是一种近似 LRU 的算法实现，可以看作是对 FIFO 算法的改进。

Clock 页面置换算法

为什么需要 clock 算法？

LRU算法的性能接近于OPT,但是实现起来比较困难，且开销大；FIFO算法实现简单，但性能差。

所以操作系统的设计者尝试了很多算法，试图用比较小的开销接近LRU的性能，这类算法都是CLOCK算法的变体。

由于该算法循环地检查各页面的情况，故称为CLOCK算法，又称为最近未用(Not Recently Used, NRU)算法。

基本思路

需要用到页表项的访问位（access bit），当一个页面被装入内存时，把该位初始化为0，然后如果这个页被访问（读/写）时，硬件把它置为1.

把各个页面组织成环形链表（类似钟表面），把指针指向最老的页面（最先进来）；

当发生一个缺页中断，考察指针所指向的最老的页面，若它的访问为为0，则立即淘汰。若访问为1，则把该位置为0，然后指针往下移动一格。如此下去，直到找到被淘汰的页面，然后把指针移动到它的下一格。

个人疑惑

（1）如果找了一圈发现元素都是 1 怎么办？

是不是直接默认取第一个元素，这样认为就是回到了朴素的 FIFO 机制。

（2）访问的性能问题

这里的遍历可以认为是一个循环链表：

每一个节点内容：

K key;
boolean accessFlag;

朴素的 FIFO 非常简单，直接往队列中扔元素就行，然后淘汰最老的一个元素。

这个如果真的使用链表作为数据结构，那么查找，更新时间复杂度就是 O(N)，显然性能一般。

能想到的方案就是 HashMap 中存储 key+双向链表节点。

和性能改进版本的 LRU 对比，就是每次更新不做节点的移除调整，而只是更新对应的标志位。

简单的CLOCK算法

是通过给每一个访问的页面关联一个附加位(reference bit)，有些地方也叫做使用位(use bit)。

他的主要思想是：当某一页装入主存时，将use bit初始化为0；如果该页之后又被访问到，使用位也还是标记成1。

对于页面置换算法，候选的帧集合可以看成是一个循环缓冲区，并且有一个指针和缓冲区相关联。遇到页面替换时，指针指向缓冲区的下一帧。

如果这页进入主存后发现没有空余的帧(frame)，即所有页面的使用位均为1，那么这时候从指针开始循环一个缓冲区，将之前的使用位都清0，并且留在最初的位置上，换出该桢对应的页。

ps: 这里发现没有空余的帧，会将所有使用位都清零。

例子

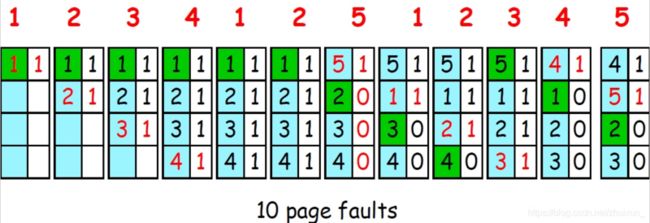
以下面这个页面置换过程为例，访问的页面依次是:1,2,3,4,1,2,5,1,2,3,4,5。

主存有4个空闲的帧，每个页面对应的结构为(页面号，使用位)。

最开始页面号1进入主存，主存里面有空闲的帧，将其使用位记成1，由于主存中之前没有页面1，所以会发生缺页中断。

同理随后的页面2，3，4进入主存，将其使用位记成1，发生缺页中断。

当之后的页面1，2进入主存时，由于页面1,2已经在主存中，不做处理。

当之后的页面5进入主存时，主存内没有空余的帧，这时候随着指针循环移动整个缓冲区，将之前页面的使用位全部清0，即这时候页面1,2,3,4对应的使用位全部为0，指针回到最初的位置，将页面1替换出去，页面5换入主存，同时使用位标记成1。

以此类推，可知CLOCK共发生10次缺页中断。

Gclock(Generalized clock page replacement algorithm)

算法思想

该算法是Clock的变种。

相对于Clock标志位采用的是二进制0和1表示，Gclock的标志位采用的是一个整数，意味着理论上可以一直增加到无穷大。

工作原理

（1）当待缓存对象在缓存中时，把其标记位的值加1。同时，指针指向该对象的下一个对象。

（2）若不在缓存中时，检查指针指向对象的标记位。如果是0，则用待缓存对象替换该对象；否则，把标记位的值减1，指针指向下一个对象。如此直到淘汰一个对象为止。由于标记位的值允许大于1，所以指针可能循环多遍才淘汰一个对象。

ps: 这个有点类似于简化版本的 LFU，统计了对应的出现次数。

WSclock(Working set clock page replacement algorithm)

算法思想

该算法同样是clock的变种，可能是实际运用最广泛的算法。

它采用clock的原理，是ws算法的增强版。

算法数据结构为循环链表，每个缓存对象保存了"最近使用的时间"rt和"是否引用"的R标志位,使用一个周期计时器t。age表示为当前时间和rt的差值

工作原理

（1）当待缓存对象存在缓存中时，更新rt为当前时间。同时，指针指向该对象的下一个对象。

（2）若不存在于缓存中时，如果缓存没满，则更新指针指向位置的rt为当前时间,R为1。同时，指针指向下一个对象。如果满了，则需要淘汰一个对象。检查指针指向的对象，

• R为1，说明对象在working set中，则重置R为0，指针指向下一个对象。
• R为0。如果age大于t，说明对象不在working set中，则替换该对象，并置R为1，rt为当前时间。如果age不大于t，则继续寻找淘汰对象。如果回到指针开始的位置，还未寻找到淘汰对象，则淘汰遇到的第一个R为0的对象。

二次机会法（或者enhanced clock）

改进型的CLOCK算法

思路：减少修改页的缺页处理开销

修改Clock算法，使它允许脏页总是在一次时钟头扫描中保留下来，同时使用脏位（dity bit,也叫写位）和使用位来指导置换

算法流程

在之前的CLOCK算法上面除了使用位(used bit)，还增加了一个修改位(modified bit)，有些地方也叫做dirty bit。

现在每一页有两个状态，分别是(使用位，修改位)，可分为以下四种情况考虑：

(0,0)：最近没有使用使用也没有修改，最佳状态！

(0,1)：修改过但最近没有使用，将会被写

(1,0)：使用过但没有被修改，下一轮将再次被用

(1,1)：使用过也修改过，下一轮页面置换最后的选择

例子

以下面这个页面置换过程为例：

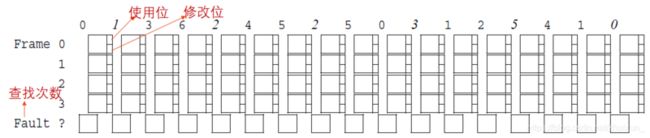
访问的页面依次是:0,1,3,6,2,4,5,2,5,0,3,1,2,5,4,1,0，其中红色数字表示将要修改的页面，即他们的modified bit将被设置成1，在下图中这些页面用斜体表示，使用位和修改位如下图所示。下面的"Fault ?"表示缺页时查找空闲frame的次数。

替换顺序

1. 从指针当前的位置开始寻找主存中满足(使用位，修改位)为(0,0)的页面；
2. 如果第1步没有找到满足条件的，接着寻找状态为(0,1)页面；
3. 如果依然没有找到，指针回到最初的位置，将集合中所有页面的使用位设置成0。重复第1步，并且如果有必要，重复第2步，这样一定可以找到将要替换的页面。

java 实现 clock 算法

说明

本文主要实现一个简单版本的 clock 算法，并对常规的实现加上一定的性能优化。（全网可能是独家的，或者说第一个这么实现的）

优化主要是基于性能的考虑，类似于前面对于 LRU 的性能优化，将查询操作从 O(N) 优化到 O(1)。

实现思路

我们定义一个符合当前业务场景的循环链表（这个后期也可以独立出去，有时间单独写一个数据结构项目，便于复用）

定义包含 accessFlag 的节点。

我们使用双向链表，而不是单向链表，这样删除的性能是最好的。

使用 map 保存 key 的信息，避免循环整个链表判断 key 是否存在，用空间换取时间。

好了，接下来就是快乐的编码阶段了。

代码实现

节点定义

/**
 * 循环链表节点
 * @author binbin.hou
 * @since 0.0.15
 * @param  key
 * @param  value
 */
public class CircleListNode {

    /**
     * 键
     * @since 0.0.15
     */
    private K key;

    /**
     * 值
     * @since 0.0.15
     */
    private V value = null;

    /**
     * 是否被访问过
     * @since 0.0.15
     */
    private boolean accessFlag = false;

    /**
     * 后一个节点
     * @since 0.0.15
     */
    private CircleListNode pre;

    /**
     * 后一个节点
     * @since 0.0.15
     */
    private CircleListNode next;

    //getter & setter
}

这里很简单的几个元素：key, value, accessFlag（是否访问过的标识），然后就是 next, pre 用户实现双向链表。

双向链表实现

基本属性

为了和原来的 Lru 双向链表保持一致，我们实现原来的额接口。

public class LruMapCircleList implements ILruMap {

    private static final Log log = LogFactory.getLog(LruMapCircleList.class);

    /**
     * 头结点
     * @since 0.0.15
     */
    private CircleListNode head;

    /**
     * 映射 map
     * @since 0.0.15
     */
    private Map> indexMap;

    public LruMapCircleList() {
        // 双向循环链表
        this.head = new CircleListNode<>(null);
        this.head.next(this.head);
        this.head.pre(this.head);

        indexMap = new HashMap<>();
    }

}

初始化 Head 节点，indexMap 用户保存 key 和双向节点之间的关系。

删除元素

/**
 * 移除元素
 *
 * 1. 是否存在，不存在则忽略
 * 2. 存在则移除，从链表+map中移除
 *
 * head==>1==>2==>head
 *
 * 删除 2 之后：
 * head==>1==>head
 * @param key 元素
 * @since 0.0.15
 */
@Override
public void removeKey(final K key) {
    CircleListNode node = indexMap.get(key);
    if(ObjectUtil.isNull(node)) {
        log.warn("对应的删除信息不存在：{}", key);
        return;
    }
    CircleListNode pre = node.pre();
    CircleListNode next = node.next();
    //1-->(x2)-->3  直接移除2
    pre.next(next);
    next.pre(pre);
    indexMap.remove(key);
    log.debug("Key: {} 从循环链表中移除", key);
}

节点的删除不难，直接从循环链表中移除节点即可，同时移除 indexMap 中的信息。

更新

此处对于 put/get 用的是同一个方法，实际上如果想实现增强版本的 clock 算法，二者还是区分开比较好，不过个人感觉原理差不多，此处就不再实现了，估计这就是淘汰算法的最后一个小节。

/**
 * 放入元素
 *
 * 类似于 FIFO，直接放在队列的最后
 * 
 * head==>1==>head
 * 加入元素：
 *
 * head==>1==>2==>head
 *
 * （1）如果元素不存在，则直接插入。
 * 默认 accessFlag = 0;
 * （2）如果已经存在，则更新 accessFlag=1;
 *
 * @param key 元素
 * @since 0.0.15
 */
@Override
public void updateKey(final K key) {
    CircleListNode node = indexMap.get(key);
    // 存在
    if(ObjectUtil.isNotNull(node)) {
        node.accessFlag(true);
        log.debug("节点已存在，设置节点访问标识为 true, key: {}", key);
    } else {
        // 不存在，则插入到最后
        node = new CircleListNode<>(key);
        CircleListNode tail = head.pre();
        tail.next(node);
        node.pre(tail);
        node.next(head);
        head.pre(node);
        // 放入 indexMap 中，便于快速定位
        indexMap.put(key, node);
        log.debug("节点不存在，新增节点到链表中：{}", key);
    }
}

这里主要就是区分下节点是否已经存在。

（1）已存在，直接获取节点，更新 accessFlag=true;

（2）不存在：插入新的节点，accessFlag = false

淘汰数据

/**
 * 删除最老的元素
 *
 * （1）从 head.next 开始遍历，如果元素 accessFlag = 0，则直接移除
 * （2）如果 accessFlag=1，则设置其值为0，循环下一个节点。
 *
 * @return 结果
 * @since 0.0.15
 */
@Override
public ICacheEntry removeEldest() {
    //fast-fail
    if(isEmpty()) {
        log.error("当前列表为空，无法进行删除");
        throw new CacheRuntimeException("不可删除头结点!");
    }
    // 从最老的元素开始，此处直接从 head.next 开始，后续可以考虑优化记录这个 key
    CircleListNode node = this.head;
    while (node.next() != this.head) {
        // 下一个元素
        node = node.next();
        if(!node.accessFlag()) {
            // 未访问，直接淘汰
            K key = node.key();
            this.removeKey(key);
            return CacheEntry.of(key, node.value());
        } else {
            // 设置当前 accessFlag = 0,继续下一个
            node.accessFlag(false);
        }
    }
    // 如果循环一遍都没找到，直接取第一个元素即可。
    CircleListNode firstNode = this.head.next();
    return CacheEntry.of(firstNode.key(), firstNode.value());
}

直接遍历节点，遇到 accessFlag=0 的直接淘汰即可。

如果 accessFlag=1，则设置其值为0，然后继续下一个。（这里有点免死金牌只能用一次的感觉）

循环一遍都没有找到，实际上直接取 head.next 即可，降级为 FIFO。当然因为我们已经更新 accessFlag=0 了，实际上继续循环也可以。

• 实现的不足之处

这里有一个待改进点：我们不见得每次都从开始循环。这样实际上缺点比较明显，导致越先入队的元素第二次一定被淘汰，其他未被访问的元素可能会一直存在，可以用一个元素记住这个位置。（上一次被淘汰的节点的 next 节点），感觉这样才更加符合 clock 算法的思想。

还有一种方法就是不把访问过的 accessFlag 置为0，循环一圈都找不到元素直接降级为 FIFO，不过这个在大部分元素被访问之后，性能会变差。所以还是建议标记一下上次循环的位置。

调用

我们在 cache 满的时候，调用下当前循环链表即可：

import com.github.houbb.cache.api.ICache;
import com.github.houbb.cache.api.ICacheEntry;
import com.github.houbb.cache.api.ICacheEvictContext;
import com.github.houbb.cache.core.model.CacheEntry;
import com.github.houbb.cache.core.support.struct.lru.ILruMap;
import com.github.houbb.cache.core.support.struct.lru.impl.LruMapCircleList;
import com.github.houbb.log.integration.core.Log;
import com.github.houbb.log.integration.core.LogFactory;

/**
 * 淘汰策略-clock 算法
 *
 * @author binbin.hou
 * @since 0.0.15
 */
public class CacheEvictClock extends AbstractCacheEvict {

    private static final Log log = LogFactory.getLog(CacheEvictClock.class);

    /**
     * 循环链表
     * @since 0.0.15
     */
    private final ILruMap circleList;

    public CacheEvictClock() {
        this.circleList = new LruMapCircleList<>();
    }

    @Override
    protected ICacheEntry doEvict(ICacheEvictContext context) {
        ICacheEntry result = null;
        final ICache cache = context.cache();
        // 超过限制，移除队尾的元素
        if(cache.size() >= context.size()) {
            ICacheEntry  evictEntry = circleList.removeEldest();;
            // 执行缓存移除操作
            final K evictKey = evictEntry.key();
            V evictValue = cache.remove(evictKey);

            log.debug("基于 clock 算法淘汰 key：{}, value: {}", evictKey, evictValue);
            result = new CacheEntry<>(evictKey, evictValue);
        }

        return result;
    }


    /**
     * 更新信息
     * @param key 元素
     * @since 0.0.15
     */
    @Override
    public void updateKey(final K key) {
        this.circleList.updateKey(key);
    }

    /**
     * 移除元素
     *
     * @param key 元素
     * @since 0.0.15
     */
    @Override
    public void removeKey(final K key) {
        this.circleList.removeKey(key);
    }

}

其实调用的地方没什么难度，就是直接调用下方法即可。

测试

好的，代码写完我们来简单的验证一下。

测试代码

ICache cache = CacheBs.newInstance()
        .size(3)
        .evict(CacheEvicts.clock())
        .build();
cache.put("A", "hello");
cache.put("B", "world");
cache.put("C", "FIFO");
// 访问一次A
cache.get("A");
cache.put("D", "LRU");
Assert.assertEquals(3, cache.size());
System.out.println(cache.keySet());

日志

[DEBUG] [2020-10-07 11:32:55.396] [main] [c.g.h.c.c.s.s.l.i.LruMapCircleList.updateKey] - 节点不存在，新增节点到链表中：A
[DEBUG] [2020-10-07 11:32:55.398] [main] [c.g.h.c.c.s.s.l.i.LruMapCircleList.updateKey] - 节点不存在，新增节点到链表中：B
[DEBUG] [2020-10-07 11:32:55.401] [main] [c.g.h.c.c.s.s.l.i.LruMapCircleList.updateKey] - 节点不存在，新增节点到链表中：C
[DEBUG] [2020-10-07 11:32:55.403] [main] [c.g.h.c.c.s.s.l.i.LruMapCircleList.updateKey] - 节点已存在，设置节点访问标识为 true, key: A
[DEBUG] [2020-10-07 11:32:55.404] [main] [c.g.h.c.c.s.s.l.i.LruMapCircleList.removeKey] - Key: B 从循环链表中移除
[DEBUG] [2020-10-07 11:32:55.406] [main] [c.g.h.c.c.s.e.CacheEvictClock.doEvict] - 基于 clock 算法淘汰 key：B, value: world
[DEBUG] [2020-10-07 11:32:55.410] [main] [c.g.h.c.c.s.l.r.CacheRemoveListener.listen] - Remove key: B, value: world, type: evict
[DEBUG] [2020-10-07 11:32:55.411] [main] [c.g.h.c.c.s.s.l.i.LruMapCircleList.updateKey] - 节点不存在，新增节点到链表中：D
[D, A, C]

符合我们的预期。

LRU、FIFO与Clock的比较

LRU和FIFO本质都是先进先出的思路，但LRU是针对页面的最近访问时间来进行排序，所以需要在每一次页面访问的时候动态的调整各个页面之间的先后顺序（每一个页面的最近访问时间变了）；而FIFO针对页面进入内存的时间来进行排序，这个时间是固定不变的，所以页面之间的先后顺序是固定不变的。

如果程序局部性，则LRU会很好。如果内存中所有页面都没有被访问过会退化为FIFO（如页面进入内存后没有被访问，最近访问时间与进入内存的时间相同）。

LRU算法性能较好，但系统开销较大；FIFO算法的系统的开销较小，但可能发生Belady现象。

因此，择衷的办法就是Clock算法，在每一次页面访问时，它不必去动态调整页面在链表中的顺序，而仅仅是做一个标记，等待发生缺页中断的时候，再把它移动到链表的末尾。

对于内存当中未被访问的页面，Clock算法的表现与LRU一样好，而对于那些曾经访问过的页面，它不能像LRU那样记住它们的准确访问顺序。

置换算法补充

常见的置换算法，我们基本已经讲述了一遍了。

不过算法的变种，不同场景的算法也比较多，这里补充没有详解的算法，此处就不做对应的实现了。

目的为了完善整个淘汰算法的认知体系。

最佳置换算法(OPT)

最佳(Optimal, OPT)置换算法所选择的被淘汰页面将是以后永不使用的，或者是在最长时间内不再被访问的页面,这样可以保证获得最低的缺页率。

但由于人们目前无法预知进程在内存下的若千页面中哪个是未来最长时间内不再被访问的，因而该算法无法实现。

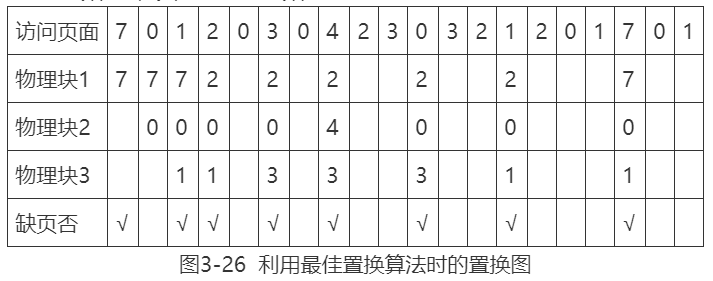
最佳置换算法可以用来评价其他算法。假定系统为某进程分配了三个物理块，并考虑有以下页面号引用串：

7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2, 1, 2, 0, 1, 7, 0, 1

进程运行时，先将7, 0, 1三个页面依次装入内存。

进程要访问页面2时，产生缺页中断，根据最佳置换算法，选择第18次访问才需调入的页面7予以淘汰。

然后，访问页面0时，因为已在内存中所以不必产生缺页中断。访问页面3时又会根据最佳置换算法将页面1淘汰……依此类推，如图3-26所示。

从图中可以看出釆用最佳置换算法时的情况。

可以看到，发生缺页中断的次数为9，页面置换的次数为6。

当然这个是理论算法，实际是无法实现的，因为我们无法预知后面的数据会被如何使用。

页面缓冲算法(PBA：Page Buffering Algorithm)　

虽然LRU和Clock置换算法都比FIFO算法好，但它们都需要一定的硬件支持，并需付出较多的开销，而且，置换一个已修改的页比置换未修改页的开销要大。

而页面缓冲算法(PBA)则既可改善分页系统的性能，又可采用一种较简单的置换策略。

VAX/VMS操作系统便是使用页面缓冲算法。它采用了前述的可变分配和局部置换方式，置换算法采用的是FIFO。

该算法规定将一个被淘汰的页放入两个链表中的一个，即如果页面未被修改，就将它直接放入空闲链表中；否则，便放入已修改页面的链表中。须注意的是，这时页面在内存中并不做物理上的移动，而只是将页表中的表项移到上述两个链表之一中。

空闲页面链表，实际上是一个空闲物理块链表，其中的每个物理块都是空闲的，因此，可在其中装入程序或数据。当需要读入一个页面时，便可利用空闲物理块链表中的第一个物理块来装入该页。当有一个未被修改的页要换出时，实际上并不将它换出内存，而是把该未被修改的页所在的物理块挂在自由页链表的末尾。

类似地，在置换一个已修改的页面时，也将其所在的物理块挂在修改页面链表的末尾。利用这种方式可使已被修改的页面和未被修改的页面都仍然保留在内存中。当该进程以后再次访问这些页面时，只需花费较小的开销，使这些页面又返回到该进程的驻留集中。当被修改的页面数目达到一定值时，例如64个页面，再将它们一起写回到磁盘上，从而显著地减少了磁盘I/O的操作次数。

一个较简单的页面缓冲算法已在MACH操作系统中实现了，只是它没有区分已修改页面和未修改页面。

置换算法对比

算法	注释
最优算法	不可实现，但可作为基准
NRU（最近未使用）算法	LRU的粗糙的近似
FIFO算法	可能抛弃重要（常使用）页面
第二次机会算法	比FIFO有大的改善
时钟算法	现实的
LRU（最近最少使用）算法	很优秀，但难以实现
NFU（最不经常使用）算法	LRU的近似
老化算法	非常近似LRU
工作集算法	实现起来开销很大
工作集时钟算法	好的有效算法

小结

clock 算法算是一种权衡，在实际的实践应用中，操作系统选择的就是这种算法。

个人理解clock 的好处就是不用频繁地每次访问都去更新元素的位置，只需要淘汰的时候进行一次更新即可，我们在 LRU 中虽然使用双向链表优化，时间复杂度为 O(1)，但是还是比较浪费的。

缓存的淘汰算法到这里基本是告一段落了，感谢你的支持，愿你有所收获。

开源地址： https://github.com/houbb/cache

觉得本文对你有帮助的话，欢迎点赞评论收藏关注一波。你的鼓励，是我最大的动力~

不知道你有哪些收获呢？或者有其他更多的想法，欢迎留言区和我一起讨论，期待与你的思考相遇。