7 道高频面试算法题,你都会了吗?「矩阵 + 位运算 + LRU」
![]()
Attention
- 秋招接近尾声,我总结了
牛客、WanAndroid上,有关笔试面经的帖子中出现的算法题,结合往年考题写了这一系列文章,所有文章均与LeetCode进行核对、测试。欢迎食用
本文将覆盖 「二进制」 + 「位运算」 和 Lru 方面的面试算法题,文中我将给出:
- 面试中的题目
- 解题的思路
- 特定问题的技巧和注意事项
- 考察的知识点及其概念
- 详细的代码和
解析
开始之前,我们先看下会有哪些重点案例:
为了方便大家跟进学习,我在 GitHub 建立了一个仓库
-
仓库地址:超级干货!精心归纳
视频、归类、总结,各位路过的老铁支持一下!给个 Star !
-
现在就让我们开始吧!
1. 矩阵
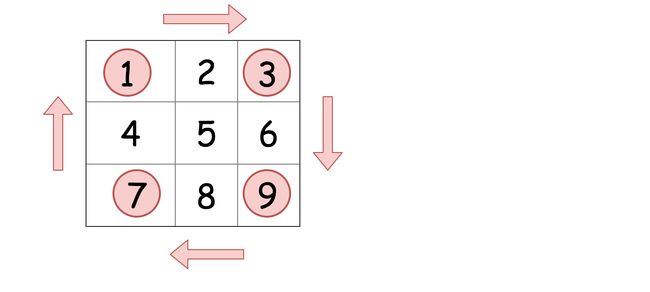
1.1 螺旋矩阵
-
给定一个包含
m x n个要素的矩阵,(m行,n列),按照螺旋顺序,返回该矩阵中的所有要素。 -
示例 :
输入:
[
[1, 2, 3, 4],
[5, 6, 7, 8],
[9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]
1.1.1 解题思路
- 我们定义矩阵的第 k 层是到最近边界距离为 k 的所有顶点。例如,下图矩阵最外层元素都是
第 1 层,次外层元素都是第 2 层,然后是第 3 层的。
[[1, 1, 1, 1, 1, 1, 1],
[1, 2, 2, 2, 2, 2, 1],
[1, 2, 3, 3, 3, 2, 1],
[1, 2, 2, 2, 2, 2, 1],
[1, 1, 1, 1, 1, 1, 1]]
-
对于每层,我们从左上方开始以顺时针的顺序遍历所有元素,假设当前层左上角坐标是 (r1, c1) \text{(r1, c1)} (r1, c1),右下角坐标是 (r2, c2) \text{(r2, c2)} (r2, c2)。
-
首先,遍历上方的所有元素
(r1, c),按照c = c1,...,c2的顺序。然后遍历右侧的所有元素(r, c2),按照r = r1+1,...,r2的顺序。如果这一层有四条边(也就是r1 < r2并且c1 < c2),我们以下图所示的方式遍历下方的元素和左侧的元素。
public List < Integer > spiralOrder(int[][] matrix) {
List ans = newArrayList();
if (matrix.length == 0)
return ans;
int r1 = 0, r2 = matrix.length - 1;
int c1 = 0, c2 = matrix[0].length - 1;
while (r1 <= r2 && c1 <= c2) {
for (int c = c1; c <= c2; c++) ans.add(matrix[r1][c]);
for (int r = r1 + 1; r <= r2; r++) ans.add(matrix[r][c2]);
if (r1 < r2 && c1 < c2) {
for (int c = c2 - 1; c > c1; c--) ans.add(matrix[r2][c]);
for (int r = r2; r > r1; r--) ans.add(matrix[r][c1]);
}
r1++;
r2--;
c1++;
c2--;
}
return ans;
}
1.2 判断数独是否合法
-
请判定一个
数独是否有效。该数独可能只填充了部分数字,其中缺少的数字用 . 表示。 -
维护一个
HashSet用来记同一行、同一列、同一九宫格是否存在相同数字
![]()
- 示例 :
输入:
[
["8","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
输出: false
解释: 除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。
但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
- 说明:
- 一个有效的数独(部分已被填充)
不一定是可解的。 - 只需要根据以上规则,验证已经填入的数字是否
有效即可。 - 给定数独序列只包含数字
1-9和字符'.'。 - 给定数独永远是
9x9形式的。`
1.2.1 解题思路
-
首先,让我们来讨论下面两个问题:
-
如何枚举子数独 ?
-
可以使用
box_index = (row / 3) * 3 + columns / 3,其中 / 是整数除法。
-
如何确保行 / 列 / 子数独中没有重复项?
-
可以利用
value -> count哈希映射来跟踪所有已经遇到的值。 -
现在,我们完成了这个算法的所有准备工作:
- 遍历数独。
- 检查看到每个单元格值是否已经在当前的行 / 列 / 子数独中出现过:
- 如果出现重复,返回
false。 - 如果没有,则保留此值以进行进一步跟踪。
- 返回
true。
public boolean isValidSudoku(char[][] board) {
Set seen = new HashSet();
for (int i=0; i<9; ++i) {
for (int j=0; j<9; ++j) {
char number = board[i][j];
if (number != '.')
if (!seen.add(number + " in row " + i) ||
!seen.add(number + " in column " + j) ||
!seen.add(number + " in block " + i / 3 + "-" + j / 3))
return false;
}
}
return true;
}
1.3 旋转图像
-
给定一个
N×N的二维矩阵表示图像,90度顺时针旋转图像。 -
示例 :
输入: [[1,1,0,0],[1,0,0,1],[0,1,1,1],[1,0,1,0]]
输出: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
解释: 首先翻转每一行: [[0,0,1,1],[1,0,0,1],[1,1,1,0],[0,1,0,1]];
然后反转图片: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
- 说明:
1 <= A.length = A[0].length <= 20
0 <= A[i][j] <= 1
1.3.1 解题思路
- 我们先来看看每个元素在旋转的过程中是如何移动的:
- 这提供给我们了一个思路,将给定的矩阵分成四个矩形并且将原问题划归为
旋转这些矩形的问题。
- 现在的解法很直接 – 可以在第一个矩形中移动元素并且在 长度为 4 个元素的临时列表中
移动它们。
public void rotate(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return;
}
int length = matrix.length;
for (int i = 0; i < length / 2; i++) {
for (int j = 0; j < (length + 1) / 2; j++){
int tmp = matrix[i][j];
matrix[i][j] = matrix[length - j - 1][i];
matrix[length -j - 1][i] = matrix[length - i - 1][length - j - 1];
matrix[length - i - 1][length - j - 1] = matrix[j][length - i - 1];
matrix[j][length - i - 1] = tmp;
}
}
}
2. 二进制 / 位运算
优点:
特定情况下,计算方便,速度快,被支持面广
如果用算数方法,速度慢,逻辑复杂
位运算不限于一种语言,它是计算机的基本运算方法
2.1 知识点预热
2.2. 只出现一次的数字
-
给出
2 * n + 1个数字,除其中一个数字之外其他每个数字均出现两次,找到这个数字。 -
异或运算具有很好的性质,相同数字异或运算后为0,并且具有交换律和结合律,故将所有数字异或运算后即可得到只出现一次的数字。
-
示例 :
输入: [4,1,2,1,2]
输出: 4
2.2.1 解题思路
-
如果我们对 0 和二进制位做 XOR 运算,得到的仍然是这个二进制位
a ⊕ 0 = a a \oplus 0 = a a⊕0=a a ⊕ 0 = a a⊕0=a a⊕0=a -
如果我们对相同的二进制位做 XOR 运算,返回的结果是 0
a ⊕ a = 0 a \oplus a = 0 a⊕a=0 a ⊕ a = 0 a⊕a=0 a⊕a=0 -
XOR 满足交换律和结合律
a ⊕ b ⊕ a = ( a ⊕ a ) ⊕ b = 0 ⊕ b = b a ⊕ b ⊕ a = ( a ⊕ a ) ⊕ b = 0 ⊕ b = b a \oplus b \oplus a = (a \oplus a) \oplus b = 0 \oplus b = ba⊕b⊕a=(a⊕a)⊕b=0⊕b=b a⊕b⊕a=(a⊕a)⊕b=0⊕b=ba⊕b⊕a=(a⊕a)⊕b=0⊕b=b -
所以我们只需要将
所有的数进行 XOR 操作,得到那个唯一的数字。
public int singleNumber(int[] A) {
if(A == null || A.length == 0) {
return -1;
}
int rst = 0;
for (int i = 0; i < A.length; i++) {
rst ^= A[i];
}
return rst;
}
2.2.2 复杂度分析
- 时间复杂度:
O(n)。我们只需要将 nums \text{nums} nums 中的元素遍历一遍,所以时间复杂度就是 nums \text{nums} nums 中的元素个数。 - 空间复杂度:
O(1)。
2.3 格雷编码
- 格雷编码是一个二进制数字系统,在该系统中,两个连续的数值仅有一个二进制的差异。给定一个
非负整数 n,表示该代码中所有二进制的总数,请找出其格雷编码顺序。一个格雷编码顺序必须以0开始,并覆盖所有的2n个整数。例子——输入:2;输出:[0, 1, 3, 2];解释:0 - 00,1 - 01,3 - 11,2 - 10
2.3.1 解题思路
- 格雷码生成公式:
G(i) = i ^ (i >> 2)
public ArrayList grayCode(int n) {
ArrayList result = new ArrayList();
for (int i = 0; i < (1 << n); i++) {
result.add(i ^ (i >> 1));
}
return result;
}
3 其他
3.1 整数反转
-
将一个整数中的数字进行
颠倒,当颠倒后的整数溢出时,返回 0 (标记为 32 位整数)。 -
示例 :
输入: -123
输出: -321
3.1.1 解题思路
- 利用
除 10 取余的方法,将最低位和最高倒序输出即可
public int reverseInteger(int n) {
int reversed_n = 0;
while (n != 0) {
int temp = reversed_n * 10 + n % 10;
n = n / 10;
if (temp / 10 != reversed_n) {
reversed_n = 0;
break;
}
reversed_n = temp;
}
return reversed_n;
}
3.2 LRU缓存策略
-
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
-
获取数据
get(key)- 如果密钥(key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。
写入数据put(key, value)- 如果密钥不存在,则写入其数据值。当缓存容量达到上限时,它应该在写入新数据之前删除最近最少使用的数据值,从而为新的数据值留出空间。 -
示例:
LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得密钥 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得密钥 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4
3.2.1 解题思路
解法一:
- 自定义数据结构:
- 实现一个链表用于记录缓存,并处理调用使用频率
- 定义一个
HashMap用于记录缓存内容
public class LRUCache {
private class Node{
Node prev;
Node next;
int key;
int value;
public Node(int key, int value) {
this.key = key;
this.value = value;
this.prev = null;
this.next = null;
}
}
private int capacity;
private HashMap<Integer, Node> hs = new HashMap<Integer, Node>();
private Node head = new Node(-1, -1);// 头
private Node tail = new Node(-1, -1);// 尾
public LRUCache(int capacity) {
this.capacity = capacity;
tail.prev = head;
head.next = tail;
}
public int get(int key) {
if( !hs.containsKey(key)) {
//key找不到
return -1;
}
// remove current
Node current = hs.get(key);
current.prev.next = current.next;
current.next.prev = current.prev;
// move current to tail
move_to_tail(current); //每次get,使用次数+1,最近使用,放于尾部
return hs.get(key).value;
}
public void set(int key, int value) {
//数据放入缓存
// get 这个方法会把key挪到最末端,因此,不需要再调用 move_to_tail
if (get(key) != -1) {
hs.get(key).value = value;
return;
}
if (hs.size() == capacity) {
//超出缓存上限
hs.remove(head.next.key); //删除头部数据
head.next = head.next.next;
head.next.prev = head;
}
Node insert = new Node(key, value); //新建节点
hs.put(key, insert);
move_to_tail(insert); //放于尾部
}
private void move_to_tail(Node current) {
//移动数据至尾部
current.prev = tail.prev;
tail.prev = current;
current.prev.next = current;
current.next = tail;
}
}
解法二:
-
题目要求实现
LRU缓存机制,需要在O(1)时间内完成如下操作: -
获取键 / 检查键是否存在
-
设置键
-
删除最先插入的键
-
前两个操作可以用标准的哈希表在
O(1)时间内完成。
-
有一种叫做
有序字典的数据结构,综合了哈希表和链表,在 Java 中为LinkedHashMap。 -
下面用这个数据结构来实现。
class LRUCache extends LinkedHashMap<Integer, Integer>{
private int capacity;
public LRUCache(int capacity) {
super(capacity, 0.75F, true);
this.capacity = capacity;
}
public int get(int key) {
return super.getOrDefault(key, -1);
}
public void put(int key, int value) {
super.put(key, value);
}
@Override
protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
return size() > capacity;
}
}
3.2.2 复杂度分析
- 时间复杂度:对于 put 和 get 操作复杂度是 O ( 1 ) O(1) O(1),因为有序字典中的所有操作:
get/in/set/move_to_end/popitem(get/containsKey/put/remove)都可以在常数时间内完成。
空间复杂度: O ( c a p a c i t y ) O(capacity) O(capacity),因为空间只用于有序字典存储最多 capacity + 1 个元素。
4 Attention
- 为了提高文章质量,防止冗长乏味
下一部分算法题
-
本片文章篇幅总结越长。我一直觉得,一片过长的文章,就像一堂超长的 会议/课堂,体验很不好,所以我打算再开一篇文章
-
在后续文章中,我将继续针对
链表栈队列堆动态规划矩阵位运算等近百种,面试高频算法题,及其图文解析 + 教学视频 + 范例代码,进行深入剖析有兴趣可以继续关注 _yuanhao 的编程世界 -
不求快,只求优质,每篇文章将以 2 ~ 3 天的周期进行更新,力求保持高质量输出
相关文章
面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」之 字符串处理+动态规划 合集!
「面试高频」二叉搜索树+双指针+贪心 算法题指北
面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」之 二分 + 哈希表 + 堆 + 优先队列 部分!
面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」必问之 链表 + 栈 + 队列 部分!
? 面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」必问之 排序 + 二叉树 部分!?
高效解决「SQLite」数据库并发访问安全问题,只这一篇就够了
每个人都要学的图片压缩终极奥义,有效解决 Android 程序 OOM
Android 让你的 Room 搭上 RxJava 的顺风车 从重复的代码中解脱出来
ViewModel 和 ViewModelProvider.Factory:ViewModel 的创建者
单例模式-全局可用的 context 对象,这一篇就够了
请点赞!因为你的鼓励是我写作的最大动力!
![]()
为了方便大家跟进学习,我在 GitHub 建立了一个仓库
仓库地址:超级干货!精心归纳视频、归类、总结,各位路过的老铁支持一下!给个 Star !