目前在做等值线等值面相关的功能,用户可拖拽控制点修改等值线,再用等值线生成等值面。因为初始的等值线点数据太多,不利于用户操作,所以先使用道格拉斯-普克算法(Douglas–Peucker)进行等值线抽稀,再将抽稀后的控制点使用贝塞尔曲线算法进行平滑。
对于贝塞尔曲线算法的平滑过程,有人做了很详细的示意图,推荐大家看下贝塞尔曲线算法之JS获取点
可以了解到贝赛尔曲线算法平滑得到的曲线是经过起始点的,同时二阶算法需要三个点,三阶算法需要四个点,四阶算法需要五个点,以此类推。
一般的来说,三阶贝塞尔曲线就已经够用了,而且效果还不错,所以我选择了三次贝塞尔曲线平滑算法来进行控制点的平滑处理。
贝塞尔曲线平滑后的等值线是基本不经过控制点的,考虑到用户操作逻辑,以及点线关系(我的控制点是等值线抽稀得到的,所以等值线是经过控制点的),所以采用三次贝塞尔曲线过点平滑算法来进行控制点的平滑处理。
过点平滑的原理就是以相邻两个控制点为起始点,然后往起始点中间插入其他过程点(不是在起始点直线上选择点),这样平滑得到的曲线是经过起始点的,而曲线如何平滑是由插入的点来控制的,三次贝塞尔曲线需要四个点,那就需要在起始点中间插入两个点。
大致思路就是,先算出相邻原始点的中点,在把相邻中点连成的线段平移到对应的原始点,以平移后的中点作为控制点,相邻原始点为起始点画贝塞尔曲线,这样就保证了连接处的光滑。而贝塞尔曲线本身是光滑的,所以就把这些原始点用光滑曲线连起来了。具体代码及示意图如下:
代码:
function createCurve(originPoint, option){
//控制点收缩系数 ,经调试0.6较好
let scale = option.tension || 0.6;
//平滑插值插入的最大点数
let maxpoints = option.pointsPerSeg
let originCount = originPoint.length
let curvePoint = []
let midpoints = []
//生成中点
for(let i = 0 ;i < originCount - 1 ; i++){
midpoints.push([
(originPoint[i][0] + originPoint[i + 1][0])/2.0,
(originPoint[i][1] + originPoint[i + 1][1])/2.0
])
}
//平移中点
let extrapoints = []
for(let i = 1 ;i < originCount - 1 ; i++){
let backi = i - 1;
let midinmid = [
(midpoints[i][0] + midpoints[backi][0])/2.0,
(midpoints[i][1] + midpoints[backi][1])/2.0
]
let offsetx = originPoint[i][0] - midinmid[0];
let offsety = originPoint[i][1] - midinmid[1];
let extraindex = 2 * i;
extrapoints[extraindex] = [
midpoints[backi][0] + offsetx,
midpoints[backi][1] + offsety
]
//朝 originPoint[i]方向收缩
let addx = (extrapoints[extraindex][0] - originPoint[i][0]) * scale;
let addy = (extrapoints[extraindex][1] - originPoint[i][1]) * scale;
extrapoints[extraindex] = [
originPoint[i][0] + addx,
originPoint[i][1] + addy
]
let extranexti = extraindex + 1;
extrapoints[extranexti] = [
midpoints[i][0] + offsetx,
midpoints[i][1] + offsety
]
//朝 originPoint[i]方向收缩
addx = (extrapoints[extranexti][0] - originPoint[i][0]) * scale;
addy = (extrapoints[extranexti][1] - originPoint[i][1]) * scale;
extrapoints[extranexti] = [
originPoint[i][0] + addx,
originPoint[i][1] + addy
]
}
let controlPoint = []
//生成4控制点,产生贝塞尔曲线
for(let i = 1 ;i < originCount - 2 ; i++){
controlPoint[0] = originPoint[i];
let extraindex = 2 * i;
controlPoint[1] = extrapoints[extraindex + 1];
let extranexti = extraindex + 2;
controlPoint[2] = extrapoints[extranexti];
let nexti = i + 1;
controlPoint[3] = originPoint[nexti];
for(let n = maxpoints; n >= 0; n--){
//存入曲线点
curvePoint.push( bezier3func(n / maxpoints, controlPoint) );
}
}
return curvePoint
}
//三次贝塞尔曲线
function bezier3func(uu, controlP){
let partX0 = controlP[0][0] * uu * uu * uu;
let partX1 = 3 * controlP[1][0] * uu * uu * (1 - uu);
let partX2 = 3 * controlP[2][0] * uu * (1 - uu) * (1 - uu);
let partX3 = controlP[3][0] * (1 - uu) * (1 - uu) * (1 - uu);
let partX = partX0 + partX1 + partX2 + partX3;
let partY0 = controlP[0][1] * uu * uu * uu;
let partY1 = 3 * controlP[1][1] * uu * uu * (1 - uu);
let partY2 = 3 * controlP[2][1] * uu * (1 - uu) * (1 - uu);
let partY3 = controlP[3][1] * (1 - uu) * (1 - uu) * (1 - uu);
let partY = partY0 + partY1 + partY2 + partY3;
return [partX, partY]
}c++版的可以看穿过已知点画平滑曲线(3次贝塞尔曲线)
然而事情到这里并没有结束,还有坑需要填,直接使用该算法进行平滑,在实际应用中发现控制点距离近的话,平滑的曲线会有尖角或交叉现象。
这是因为插入的两个新控制点和起始控制点位置特殊,平滑后产生尖角或交叉,如下所示:
优化思路是判断四个点的关系,获取直线控制点1-新控制点1与直线控制点2-新控制点2之间的交点(如果有的话),如果交点在线段控制点1-点1中时,用交点替换点1,线段控制点2-点2同理。或者以控制点1、交点、控制点2三点,然后使用二次贝赛尔曲线算法进行平滑。新的效果示意图如下所示: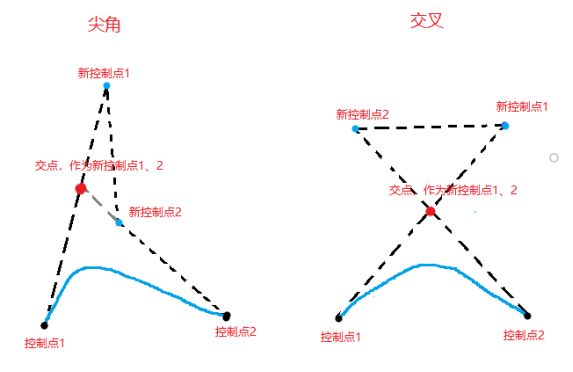
优化前与优化后的效果对比如下:左边为优化前的平滑效果,右边是优化后的平滑效果:
优化后的代码:
function createCurve(originPoint, option){
//控制点收缩系数 ,经调试0.6较好
let scale = option.tension || 0.6;
//平滑插值插入的最大点数
let maxpoints = option.pointsPerSeg
let originCount = originPoint.length
let curvePoint = []
let midpoints = []
//生成中点
for(let i = 0 ;i < originCount - 1 ; i++){
midpoints.push([
(originPoint[i][0] + originPoint[i + 1][0])/2.0,
(originPoint[i][1] + originPoint[i + 1][1])/2.0
])
}
//平移中点
let extrapoints = []
for(let i = 1 ;i < originCount - 1 ; i++){
let backi = i - 1;
let midinmid = [
(midpoints[i][0] + midpoints[backi][0])/2.0,
(midpoints[i][1] + midpoints[backi][1])/2.0
]
let offsetx = originPoint[i][0] - midinmid[0];
let offsety = originPoint[i][1] - midinmid[1];
let extraindex = 2 * i;
extrapoints[extraindex] = [
midpoints[backi][0] + offsetx,
midpoints[backi][1] + offsety
]
//朝 originPoint[i]方向收缩
let addx = (extrapoints[extraindex][0] - originPoint[i][0]) * scale;
let addy = (extrapoints[extraindex][1] - originPoint[i][1]) * scale;
extrapoints[extraindex] = [
originPoint[i][0] + addx,
originPoint[i][1] + addy
]
let extranexti = extraindex + 1;
extrapoints[extranexti] = [
midpoints[i][0] + offsetx,
midpoints[i][1] + offsety
]
//朝 originPoint[i]方向收缩
addx = (extrapoints[extranexti][0] - originPoint[i][0]) * scale;
addy = (extrapoints[extranexti][1] - originPoint[i][1]) * scale;
extrapoints[extranexti] = [
originPoint[i][0] + addx,
originPoint[i][1] + addy
]
}
let controlPoint = []
//生成4控制点,产生贝塞尔曲线
for(let i = 1 ;i < originCount - 2 ; i++){
controlPoint[0] = originPoint[i];
let extraindex = 2 * i;
controlPoint[1] = extrapoints[extraindex + 1];
let extranexti = extraindex + 2;
controlPoint[2] = extrapoints[extranexti];
let nexti = i + 1;
controlPoint[3] = originPoint[nexti];
let fn = bezier3func;
let cp = intersects(controlPoint.slice(0, 2), controlPoint.slice(-2))
if(cp && isContains(controlPoint[0], controlPoint[1], cp)){
controlPoint[1] = cp
}
if(cp && isContains(controlPoint[2], controlPoint[3], cp)){
controlPoint[2] = cp
}
if(controlPoint[1][0] == controlPoint[2][0] && controlPoint[1][1] == controlPoint[2][1]){
fn = bezier2func
controlPoint.splice(1, 1)
}
for(var n = maxpoints; n >= 0; n--){
//存入曲线点
curvePoint.push( fn(n / maxpoints, controlPoint) );
}
}
return curvePoint
}
//三次贝塞尔曲线
function bezier3func(uu, controlP){
let partX0 = controlP[0][0] * uu * uu * uu;
let partX1 = 3 * controlP[1][0] * uu * uu * (1 - uu);
let partX2 = 3 * controlP[2][0] * uu * (1 - uu) * (1 - uu);
let partX3 = controlP[3][0] * (1 - uu) * (1 - uu) * (1 - uu);
let partX = partX0 + partX1 + partX2 + partX3;
let partY0 = controlP[0][1] * uu * uu * uu;
let partY1 = 3 * controlP[1][1] * uu * uu * (1 - uu);
let partY2 = 3 * controlP[2][1] * uu * (1 - uu) * (1 - uu);
let partY3 = controlP[3][1] * (1 - uu) * (1 - uu) * (1 - uu);
let partY = partY0 + partY1 + partY2 + partY3;
return [partX, partY]
}
//二次贝塞尔曲线
function bezier2func(uu, controlP){
let partX0 = controlP[0][0] * uu * uu;
let partX1 = 2 * controlP[1][0] * uu * (1 - uu);
let partX2 = controlP[2][0] * (1 - uu) * (1 - uu);
let partX = partX0 + partX1 + partX2;
let partY0 = controlP[0][1] * uu * uu;
let partY1 = 2 * controlP[1][1] * uu * (1 - uu);
let partY2 = controlP[2][1] * (1 - uu) * (1 - uu);
let partY = partY0 + partY1 + partY2;
return [partX, partY]
}
/**
* Find a point that intersects LineStrings with two coordinates each
* 找到一个点,该点与每个线串有两个坐标相交
*/
function intersects(coords1, coords2) {
if (coords1.length !== 2) {
throw new Error(" line1 must only contain 2 coordinates");
}
if (coords2.length !== 2) {
throw new Error(" line2 must only contain 2 coordinates");
}
const x1 = coords1[0][0];
const y1 = coords1[0][1];
const x2 = coords1[1][0];
const y2 = coords1[1][1];
const x3 = coords2[0][0];
const y3 = coords2[0][1];
const x4 = coords2[1][0];
const y4 = coords2[1][1];
//斜率交叉相乘 k1 = (y4 - y3) / (x4 - x3) ... k2 = (y2 - y1) / (x2 - x1)
//k1 k2 同乘 (x4 - x3) * (x2 - x1) 得到denom
const denom = ((y4 - y3) * (x2 - x1)) - ((x4 - x3) * (y2 - y1));
const numeA = ((x4 - x3) * (y1 - y3)) - ((y4 - y3) * (x1 - x3));
const numeB = ((x2 - x1) * (y1 - y3)) - ((y2 - y1) * (x1 - x3));
if (denom === 0) { //斜率一样,平行线
return null;
}
const uA = numeA / denom;
const uB = numeB / denom;
const x = x1 + (uA * (x2 - x1));
const y = y1 + (uA * (y2 - y1));
return [x, y];
}
function isContains(sp, ep, p) {
return (
(p[0] > ep[0] && p[0] < sp[0]) || (p[0] > sp[0] && p[0] < ep[0])
) && (
(p[1] > ep[1] && p[1] < sp[1]) || (p[1] > sp[1] && p[1] < ep[1])
)
} 
