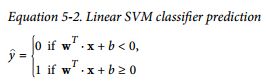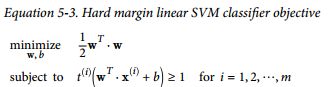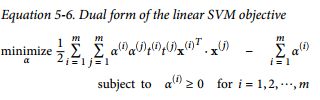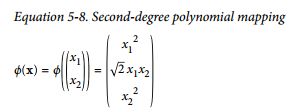核心:dual problem,kernel trick,
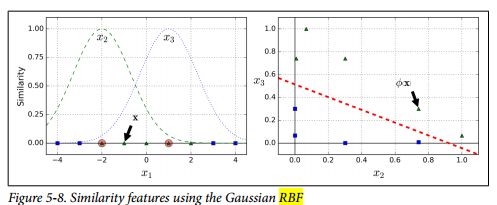
最原始的SVM是处理线性可分的情况,对于非线性可分的,可以使用soft margin SVM(不需要所有的instance都分类正确);也可以加入其他非线性的feature或者Similarity Features,强行使得线性可分,比如以下加入二阶feature后就线性可分了
上图用的是高维的Polynomial feature,下图是adding similarity feature,分别计算每个instance到左图中2个红点的距离,就把原始的一维数据转化为2维数据,而且也变得线性可分了
但是显示的加入其他高维的feature会使得计算量变大,这时就要用到kernel trick,It makes it possible to get the same result as if you added many polynomial features, even with very high-degree polynomials, without actually having to add them.
上面2种方法对应的kernel就叫Polynomial Kernel和Gaussian RBF Kernel,那kernel trick 具体是怎么样的呢?怎么把它apply到SVM中呢?
这就要引出对偶问题,因为SVM的原问题并不支持kernel trick的,SVM分类器是一个最大化间隔的分类器,对于linear SVM来说,预测是这样计算的
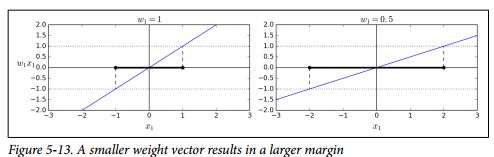
一个直观的理解就是:The smaller the weight vector w, the larger the margin
所以就可以minimize weight w
因为 ∥ w ∥is not differentiable,我们就用了上述w平方, 还有一个约束条件t(i)= –1 for negative instances (if y(i)= 0) and t(i)= 1 for positive instances (if y(i)= 1)。
这时一个QP problem,有蛮多现成的方法来解,但是因为这个原问题无法使用kernel trick(为什么后面会谈到),我们打算将原问题转化为对偶问题
The solution to the dual problem typically gives a lower bound to the solution of the primal problem, but under some conditions it can even have the same solutions as the primal problem. Luckily, the SVM problem happens to meet these conditions(KKT条件)
对应的对偶问题形式是(TODO:对偶问题的推导):
解为(TODO:为什么解是这个):
那为什么这个就可以apply kernel trick呢?先来看下kernel trick具体含义,加入我们想加入一些二阶的feature
如果计算2个转化后的feature vector的dot product的话:
可以看到The dot product of the transformed vectors is equal to the square of
the dot product of the original vectors:
这意味着:you don’t actually need to transform the training instances at all,我们只需要计算原始的2个低维向量的dot product就可以得到高维空间上的dot product,这样就可以makes the whole process much more computationally efficient,而注意到SVM的dual problem就有2个向量的点积形式,在求解和预测的时候都可以用kernel trick
b为:
In Machine Learning, a kernelis a function capable of computing the dot product ϕ(a)T·ϕ(b) based only on the original vectors aand b, without having to compute (or even to know about) the transformation ϕ,以下是一些常见的kernel
Others:
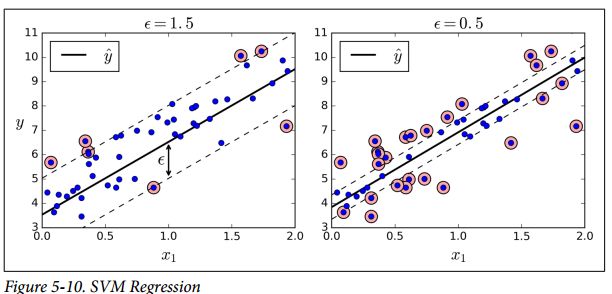
1. SVM regression:SVM Regression tries to fit as many instances as possible on the street while limiting margin violations
给定一个ϵ,目标是使得2条边界线囊括的instance越多越好
2. Linear SVM classifiercost function
第一项使得w越小越好,第二项计算的是 the total of all margin violations,The function max(0, 1 – t) is called the hinge lossfunction
Exercises
1、 Why is it important to scale the inputs when using SVMs?
SVMs try to fit the largest possible “street” between the classes (see the first answer), so if the training set is not scaled, the SVM will tend to neglect small features
2. Should you use the primal or the dual form of the SVM problem to train a model on a training set with millions of instances and hundreds of features?
This question applies only to linear SVMs since kernelized can only use the dual form. The computational complexity of the primal form of the SVM problem is proportional to the number of training instances m, while the computational complexity of the dual form is proportional to a number between m2 and m3. So if there are millions of instances, you should definitely use the primal form, because the dual form will be much too slow