去除有向图中两节点间的环

问题描述：给出点及点间的关系，指定点为根节点，把有向图转化为树。其中，有向图中的环，只是两个节点之间。比如

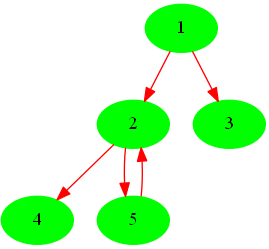   经过去掉环得到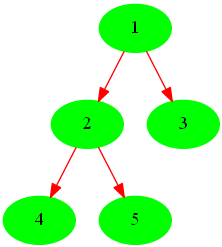   

其中图的表示为：

1->2

2->4

2->5

1->3

5->2

解决之道
先用字典node_dic把整个图表示出来；列表has_kid存放不是叶子的节点；列表node_list是个队列，存放本节点和它的孩子；列表have_exist表示已经存在的节点，对于node_list如果不是孩子节点，又不在have_exist中，当被遍历是存于have_exist，同时在node_lst删除该节点。之后遍历node_list，如果之前已经存在于have_exist中了，则删除之间的关系。剩下的部分为无环图。

示例

node_dic: {1:[2, 3], 2:[4, 5], 5:[2]}

has_kid: [1, 2, 5]

指定根节点为1

 步骤

*）一开始node_list存放根节点：(注意node_list背景色为红色，have_eist为绿色)

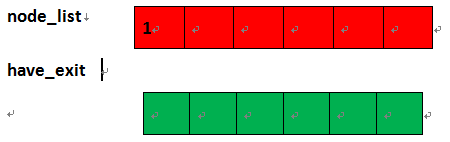
此时：node_dic: {1:[2, 3], 2:[4, 5], 5:[2]}

**）看node_list的第一个节点，不在have_exist，又不是孩子节点，把它所有的孩子存于队列node_list,查看孩子是否在have_exist，要是在就删除node_dic中的关系。最后删除首节点

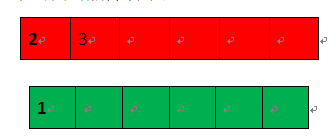
***）看node_list的第一个节点，不在have_exist，又不是孩子节点，把它所有的孩子存于队列node_list,查看孩子是否在have_exist，要是在就删除node_dic中的同时删除首节点。

 

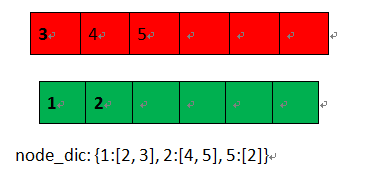
****）看node_list的第一个节点4、5，是孩子节点，直接删除该节点

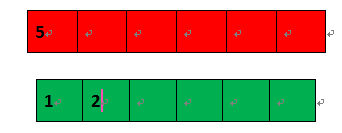
此时：node_dic: {1:[2, 3], 2:[4, 5], 5:[2]}

*****）看node_list的第一个节点，在have_exist，删除首节点,同时删除node_dice中的关系。

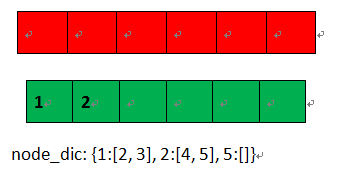
参考代码（python）

node_relation = ['1->2', '2->4', '2->5', '5->2', '1->3']

root = '1'

node_dic = {}

have_kid = []

have_exist = []

node_list = []

for key in node_relation:

    chunk = key.split("->")

    if not chunk[0] in have_kid:

        have_kid.append(chunk[0])

    if not node_dic.has_key(chunk[0]):

        node_dic[chunk[0]] = []

        node_dic[chunk[0]].append(chunk[1])

    else:

        node_dic[chunk[0]].append(chunk[1])

node_list.append(root)

while len(node_list) != 0:

    rmtmp = []

    if not node_list[0] in have_kid:

        node_list.remove(node_list[0])

    else:

        for key in node_dic[node_list[0]]:

            node_list.append(key)

            if key in have_exist:

                rmtmp.append(key)

        if node_list[0] not in have_exist:

            have_exist.append(node_list[0])

        for keyy in rmtmp:

            node_dic[node_list[0]].remove(keyy)

        node_list.remove(node_list[0])

print node_dic

    

结果：{'1': ['2', '3'], '2': ['4'], '5': []}