找出一堆整数中两个元素和为指定值的所有组合

问题描述

5, 5,-7, 5, 9, -1, 5, 1, 9, 4, 6 这堆数中两个数的和为10的组合有:5+5, 9+1, 4+6,如何快速的找出这样的组合？

假定

数组a[]存放元素，数组大小为len_a

指定和为aim

思路一

先排序，low=0(最低位置)，up=len_a(最高位置)

• 当a[low]+a[up]>aim时，hig=high-1
• 当a[low]+a[up]<aim时，low=low+1
• 当a[low]+a[up]=aim时，输出a[low]、a[up]

代码：

#include <iostream>  

#include <algorithm>  

using namespace std;  

  

void printPairSums(int data[], int size, int sum);  

int main(int argc, char* argv[])  

{  

    int data[] = {1, 5, 9, -1, 4, 6, -2, 3, -8};  

    int size = sizeof(data) / sizeof(data[0]);  

    int i;  

    sort(data, data + size);  

    printPairSums(data, size, 8);  

  

    return 0;  

}  

void printPairSums(int data[], int size, int sum)  

{  

    int first = 0;  

    int last = size -1;  

    int s = 0;  

    while (first < last)  

    {  

        s = data[first] + data[last];  

        if (s == sum)  

        {  

            cout << data[first] << " + " << data[last] << " = " << sum << endl;  

            first++;  

            last--;  

        }  

        else if (s < sum)  

        {  

            first++;  

        }  

        else  

        {  

            last--;  

        }  

    }  

}  

 

思路二

位操作（详细解释看http://www.cnblogs.com/kaituorensheng/p/3169570.html）

思路：

#include <iostream>

#include <algorithm>

using namespace std;

void setBit(char *entry, int nBits)

{

    entry[nBits/8] = entry[nBits/8] | (1 << (nBits%8));

}

void setBit_0(char *entry, int nBits)

{

    entry[nBits/8] = entry[nBits/8] & ~(1 << (nBits%8));

}


int checkBit(char *entry, int nBits)

{

    return entry[nBits/8] & (1 << (nBits%8));

}

int main()

{

    int data[] = {5,-7, 9, -1, 1, 9, 4, 6};

    int aim = 10;

    int size = sizeof(data) / sizeof(data[0]);

    int i, min=data[0], max=data[0];

    int num_aim = 0;

    if(aim % 2 == 0)

    {

        for(i=0; i<size; i++)

        {

            if (aim / 2 == data[i])

                num_aim += 1;

        }

    }



    for(i=1; i<size; i++)

    {

        if(data[i] < min)

            min = data[i];

        if(data[i] > max)

            max = data[i];

    }

    int dis_e = (max-min) / 8 + 1;

    char entry[dis_e];

    for (i=0; i<dis_e; i++)

    {

        entry[i] = 0;

    }

    int dis = 0 - min;



    for(i=0; i<size; i++)

    {

        setBit(entry, data[i]+dis);

    }



    if(aim % 2==0)

    {

        setBit_0(entry, aim/2 + dis);

        if(num_aim > 1)

            cout << data[i] << " " << (aim - data[i]) << endl;

    }

    for(i=0; i<size; i++)

    {

        if(checkBit(entry,  aim - data[i] + dis) != 0)

        {

            setBit_0(entry, data[i] + dis);

            setBit_0(entry, aim - data[i] + dis);

            cout << data[i] << " " << (aim - data[i]) << endl;

        }

    }

}

 

问题扩展

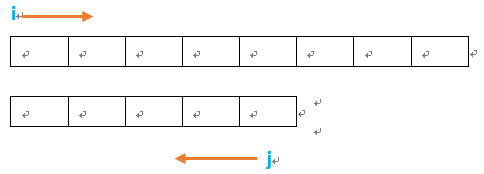
已知两个升序数组，从两个数组中各取一个数值，求使得两个数之和为给定值的所有组合。

问题本质和一位数组一样，一个从一个数组的开始前进，一个从另外一个数组的最后后退。