POJ 1470 Closest Common Ancestors （LCA，离线Tarjan算法）

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 13372		Accepted: 4340

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form: 

nr_of_vertices 
vertex:(nr_of_successors) successor1 successor2 ... successorn 
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form: 
nr_of_pairs 
(u v) (x y) ... 

The input file contents several data sets (at least one). 
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
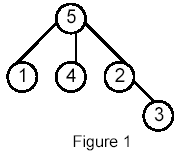
For example, for the following tree: 

Sample Input

5

5:(3) 1 4 2

1:(0)

4:(0)

2:(1) 3

3:(0)

6

(1 5) (1 4) (4 2)

      (2 3)

(1 3) (4 3)

Sample Output

2:1

5:5

Hint

Huge input, scanf is recommended.

 

 

  1 /* ***********************************************

  2 Author        :kuangbin

  3 Created Time  :2013-9-5 9:11:48

  4 File Name     :F:\2013ACM练习\专题学习\LCA\POJ1470_2.cpp

  5 ************************************************ */

  6 

  7 #include <stdio.h>

  8 #include <string.h>

  9 #include <iostream>

 10 #include <algorithm>

 11 #include <vector>

 12 #include <queue>

 13 #include <set>

 14 #include <map>

 15 #include <string>

 16 #include <math.h>

 17 #include <stdlib.h>

 18 #include <time.h>

 19 using namespace std;

 20 /*

 21  * POJ 1470

 22  * 给出一颗有向树，Q个查询

 23  * 输出查询结果中每个点出现次数

 24  */

 25 /*

 26  * LCA离线算法，Tarjan

 27  * 复杂度O(n+Q);

 28  */

 29 const int MAXN = 1010;

 30 const int MAXQ = 500010;//查询数的最大值

 31 

 32 //并查集部分

 33 int F[MAXN];//需要初始化为-1

 34 int find(int x)

 35 {

 36     if(F[x] == -1)return x;

 37     return F[x] = find(F[x]);

 38 }

 39 void bing(int u,int v)

 40 {

 41     int t1 = find(u);

 42     int t2 = find(v);

 43     if(t1 != t2)

 44         F[t1] = t2;

 45 }

 46 //************************

 47 bool vis[MAXN];//访问标记

 48 int ancestor[MAXN];//祖先

 49 struct Edge

 50 {

 51     int to,next;

 52 }edge[MAXN*2];

 53 int head[MAXN],tot;

 54 void addedge(int u,int v)

 55 {

 56     edge[tot].to = v;

 57     edge[tot].next = head[u];

 58     head[u] = tot++;

 59 }

 60 

 61 struct Query

 62 {

 63     int q,next;

 64     int index;//查询编号

 65 }query[MAXQ*2];

 66 int answer[MAXQ];//存储最后的查询结果，下标0~Q-1

 67 int h[MAXQ];

 68 int tt;

 69 int Q;

 70 

 71 void add_query(int u,int v,int index)

 72 {

 73     query[tt].q = v;

 74     query[tt].next = h[u];

 75     query[tt].index = index;

 76     h[u] = tt++;

 77     query[tt].q = u;

 78     query[tt].next = h[v];

 79     query[tt].index = index;

 80     h[v] = tt++;

 81 }

 82 

 83 void init()

 84 {

 85     tot = 0;

 86     memset(head,-1,sizeof(head));

 87     tt = 0;

 88     memset(h,-1,sizeof(h));

 89     memset(vis,false,sizeof(vis));

 90     memset(F,-1,sizeof(F));

 91     memset(ancestor,0,sizeof(ancestor));

 92 }

 93 

 94 void LCA(int u)

 95 {

 96     ancestor[u] = u;

 97     vis[u] = true;

 98     for(int i = head[u];i != -1;i = edge[i].next)

 99     {

100         int v = edge[i].to;

101         if(vis[v])continue;

102         LCA(v);

103         bing(u,v);

104         ancestor[find(u)] = u;

105     }

106     for(int i = h[u];i != -1;i = query[i].next)

107     {

108         int v = query[i].q;

109         if(vis[v])

110         {

111             answer[query[i].index] = ancestor[find(v)];

112         }

113     }

114 }

115 

116 bool flag[MAXN];

117 int Count_num[MAXN];

118 int main()

119 {

120     //freopen("in.txt","r",stdin);

121     //freopen("out.txt","w",stdout);

122     int n;

123     int u,v,k;

124     while(scanf("%d",&n) == 1)

125     {

126         init();

127         memset(flag,false,sizeof(flag));

128         for(int i = 1;i <= n;i++)

129         {

130             scanf("%d:(%d)",&u,&k);

131             while(k--)

132             {

133                 scanf("%d",&v);

134                 flag[v] = true;

135                 addedge(u,v);

136                 addedge(v,u);

137             }

138         }

139         scanf("%d",&Q);

140         for(int i = 0;i < Q;i++)

141         {

142             char ch;

143             cin>>ch;

144             scanf("%d %d)",&u,&v);

145             add_query(u,v,i);

146         }

147         int root;

148         for(int i = 1;i <= n;i++)

149             if(!flag[i])

150             {

151                 root = i;

152                 break;

153             }

154         LCA(root);

155         memset(Count_num,0,sizeof(Count_num));

156         for(int i = 0;i < Q;i++)

157             Count_num[answer[i]]++;

158         for(int i = 1;i <= n;i++)

159             if(Count_num[i] > 0)

160                 printf("%d:%d\n",i,Count_num[i]);

161     }

162     return 0;

163 }