用JavaScript玩转游戏编程(一)掉宝类型概率
问题定义
游戏(和一些模拟程序)经常需要使用随机数,去应付不同的游戏(或商业)逻辑。本文分析一个常见问题:有N类物件,设第i类物件的出现概率为P(X=i),如何产生这样的随机变量X?
例如对概率的要求是
P(X=0)=0.12
P(X=1)=0.4
P(X=2)=0.4
P(X=3)=0.07
P(X=4)=0.01
输入数组<0.12, 0.4, 0.4, 0.07, 0.01> 输出符合以上概率的随机数序列,如<1, 4, 2, 1, 2, 2, 1, 0, ...> 。
以下先谈一些统计学背景知识,再给这问题的可行解法。
概率分布
这问题要产生一个随机变量,接近指定的概率分布(probability distribution)。大部份程序语言都提供接近均匀分布(uniformly distributed)的伪随机数产生器(pseudorandom number generator, PRNG),例如JavaScript提供的Math.random()函数,可传回 [0, 1)半开区间的均匀分布伪随机数。
密度分布函数
现在,不仿测试一下JavaScript的Math.random()函数,看看它是否均匀分布。一个变数的分布以密度分布函数(probability density function, PDF)定义,一般写作f_X(x),随机变量X在区间[a,b]上的概率为定积分:
为了把PDF视觉化,可以把X分为若干区间,统计各区间X出现的频率,绘画其直方图(histogram)。笔者写了一个简单的JavaScript框架,用HTML5 Canvas绘画直方图。以下测试代码,可绘画Math.random()的PDF估值(estimate)。
在统计学中,每个数据称为取样(sample),当取样数目n越大,可以看到其PDF估值越接近平均。
读者可以试试,把x的赋值改为Math.pow(Math.random(), 2)。你会发现,PDF的分布改变了,其密度更集中于左边。读者也可以改为其他表达式(只要其输出在[0, 1)的范围),看看其分布。如果想看精确一点,也可以加大frequency数组。
累积分布函数
密度分布函数,可以变换为累积分布函数(cumulative distribution function, CDF),代表随机变量X小于x的概率:
在X为连续(continuous)的情况下,CDF可用PDF定义:
在X为离散(discrete)的情况下,CDF可定义为:
以下的pdf2cdf()函数,能把离散的PDF数组,转换为CDF数组。由于浮点小数相加会有误差,最后的值可能少于1,有机会产生bug,函数里强制指定最后一个元素为1。
function pdf2cdf(pdf) {
var cdf = pdf.slice();
for (var i = 1; i < cdf.length - 1; i++)
cdf[i] += cdf[i - 1];
// Force set last cdf to 1, preventing floating-point summing error in the loop.
cdf[cdf.length - 1] = 1;
return cdf;
}
以下代码测试绘画Math.random()的CDF估值(只把plotPdf改了為plotCdf):
均匀分布的Math.random(),其CDF估值接近斜线。
题解
这问题其实正式来说,可称为模拟离散取样(simulated discrete sampling),跟据有限类别的指定概率,来模拟取样。
要制造指定的概率分布随机变量,关键就是如何把均匀分布变换。
逆变换取样
在上节中,显示了CDF的一些特性,例如CDF的范围是[0,1],而且是一个单调递增(monotonic increasing)函数。逆变换取样(inverse transform sampling)利用了这些特性,去解决这个问题。逆变换取样方法其实很简单,给一个目标CDF,只要计算其逆函数(inverse function),就可以把均匀的随机变数转换为目标CDF:
这方法能用在所有CDF(包括连续及离散的)。其数学证明可参考维基百科。
下图显示这个方法的直观解读,在Y轴[0,1]范围里均匀取样(y_i),之后向右和CDF取交点,求交点的X轴位置(x_i),X则是符合CDF的概率分布。
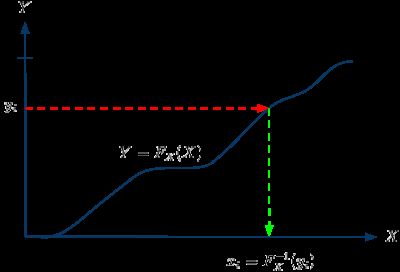
这个方法用在离散的情况就更简单,只需搜寻目标的CDF,找出超过均匀取样的元素即可。代码如下:
function discreteSampling(cdf) {
var y = Math.random();
for (var x in cdf)
if (y < cdf[x])
return x;
return -1; // should never runs here, assuming last element in cdf is 1
}
题目的测试:
分析
在离散的情况下(本文题目要求),其时间复杂度是O(N),其中N为类别数目。
读者可能会注意到,这里用了线性搜寻(linear search),如果targetPdf数组是由大至小排列,平均而言会更快找到结果。另外,也可以用二分搜寻(binary search),那么复杂度会降低为O(lg N),这留给读者作为练习。
事实上,这个问题用二分搜寻是标准的方法。那么,还有没有更快的方法呢?答案是肯定的,例如别名方法(alias method)、近似方法等,有兴趣的读者可参考[1]。当然,在N很小的情况下,线性搜寻和二分搜寻也足够。
结语
笔者以前的著作也简单提及过这个问题,不过本文加入理论背景,希望读者能更深入了解。这个问题在游戏中经常使用,例如按设计概率产生怪物、宝物,或是用来控制非玩家角色(non-playable character, NPC)的行为。模拟取样亦使用在计算机图形学上,例如粒子系统,或是采用蒙地卡罗积分法(Monte Carlo integration)的渲染算法。后者大概会在不可预计的将来,于另一系列里探讨。
笔者撰写本文,灵感来自这篇博文。其算法实际上是储存CDF的逆函数取样,利用空间和有限的CDF精确度,换取O(1)的时间复杂度。衡量N的大小、精确度、空间需求、缓存延迟后,或许该方法也能适合某些个别需求。但对于该文作者说N最大为100,二分搜寻只需最多7次迭代,因缓存问题可能二分搜寻更快。有鉴于该文未详细讨论这些需求分析、背后理论、以至代码可能对一些网友来说比较难理解,希望本文能加以补充。
这系列会探讨一些游戏编程相关的问题,例如随机相关(PRNG、洗牌、其他随机取样方法)、游戏机制相关(状态机、细包自动机)等等。网友们也可以提供一些题目,大家互相讨论学习。
本文的JavaScript完整程序可在此下载。
参考
- [1] David Cline, Anshuman Razdan, Peter Wonka. A Comparison of Tabular PDF Inversion Methods. Computer Graphics Forum. volume 28. number 1. pages 154-160. 2009
更新
- 2010-04-21 感谢livepine,修正问题定义中,数组最后一个值。
- 2010-04-26 修正下载连结