主成分分析PCA的前世今生

这篇博客会以攻略形式介绍PCA在前世今生。

    其实，主成分分析知识一种分析算法，他的前生：应用场景；后世：输出结果的去向，在网上的博客都没有详细的提示。这里，我将从应用场景开始，介绍到得出PCA结果后，接下来的后续操作。

 

前世篇

  

我们要先从多元线性回归开始。对图9-3作一下多远线性回归

X1——总产值，X2——存储量，X3——总消费，Y——进口总额

从最直白的讲，对Y进行多元线性回归分析，就是在X1，X2，X3前加个系数，然后总体相加的结果，越接近越好。

用R的多远线性归回方法分析看看：

conomy<-data.frame(

  x1=c(149.3, 161.2, 171.5, 175.5, 180.8, 190.7,202.1, 212.4, 226.1, 231.9, 239.0),

  x2=c(4.2, 4.1, 3.1, 3.1, 1.1, 2.2, 2.1, 5.6, 5.0, 5.1, 0.7),

  x3=c(108.1, 114.8, 123.2, 126.9, 132.1, 137.7,

       146.0, 154.1, 162.3, 164.3, 167.6),

  y=c(15.9, 16.4, 19.0, 19.1, 18.8, 20.4, 22.7,

      26.5, 28.1, 27.6, 26.3)

)



lm.sol <- lm(y~x1+x2+x3, data=conomy)

summary(lm.sol)

结果：

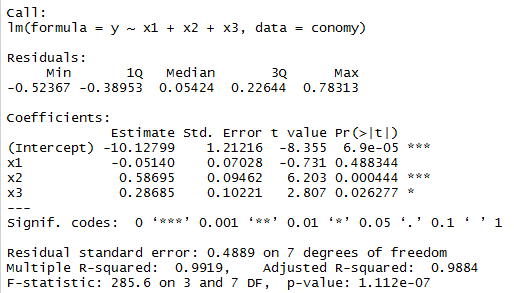
因此，通过简单粗暴（未经删选变量）的线性回归分析，也可以得出结果Y=-10.12799-0.0514X1+0.58695X2+0.28685X3，

但我们发现X1没有*（sigif，*越多越好），而且X1的系数是负数，就是说国内总产值越高，进口量却降低，

其主要原因是三个变量存在多重共线性，矩阵的行列式接近0。

所以，就引发了一个问题，如何筛选有效变量和降维，这里就要正式介绍主成分分析算法了。

 

主成分分析的今生

 Pearson于1901年提出，再由Hotelling（1933）加以发展的一种多变量统计方法

 通过析取主成分显出最大的个别差异，也用来削减回归分析和聚类分析中变量的数目

 可以使用样本协方差矩阵或相关系数矩阵作为出发点进行分析

 成分的保留：Kaiser主张（1960）将特征值小于1的成分放弃，只保留特征值大于1的成分

 如果能用不超过3-5个成分就能解释变异的80%，就算是成功

主成分实际研究的是变量与变量之间的关系，不管你有多少样本，其相关矩阵只和样本的维度有关。比如上例中，X1，X2，X3是维度，1~11是样本数。主成分分析第一步获取样本的协方差阵：而且显然cov（Xi，Xj）=cov（Xj，Xi）。

 

根据矩阵定理，实对角矩阵必定存在正交矩阵Q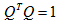（），使得：

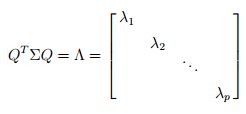这里的∑即协方差矩阵。

因为我们要筛选最能表现Y的X分量，从集合意义上来说，就是找X之间差异最大的，比如要体现“人”的特点

，那么找一个黑人和一个白人的观测值，要比找两个白人好。而表现差异的统计量，我们在初中就接触过，

不错，就是方差（或标准差），接下来我们要找协方差之间差距（方差）最大的变量。

 

数学家又来刷存在感了：

                         
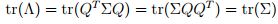
有上式可以推到出：

                            

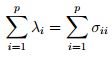
这里λi就是特征值，σii就是第i个对角元素，表明特征值λ可以表示X之间的方差，即X之间的差异程度，在F1方向上的X分量最大。

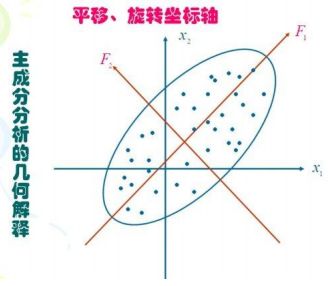
好了，现在我们缕一缕思路，要找可以表示Y的最好X变量，我们现在已经找到了差距最大的两两X分量（λ最大），

可以把X1和X2的差距看成是在F1轴上的距离，接下来，我们要做的是把X1，X2映射（投影）到F1，F2轴上，

即用F=a1*X1+a2*X2的形式。我们惊奇的发现，a1，a2构成的向量正好就是协方差对应的特征向量！！！

 

顺理成章的，我们求得特征向量A[a1,a2,a3,a4,a5……an]，这里要说明的是，λ从大到小排列后，

A中的an是对应λ的特征向量。至此，关于X的主成分分析完成，找到了相互正交的特征向量A（矩阵定理：实对称矩阵的特征向量两两正交）。

好的，我们用matalb和R分别实现。

matlab：

1，自己实现

A=[1 2 3 4 5

    4 2 3 6 1

     5 8 11 4 6];%自定义矩阵

 [n,p]=size(A);
 AA=cov(A)%求A的协方差矩阵


 [T,lambda]=eig(AA);%T是特征向量，lambda是特征值

lambda=diag(lambda); % p*1向量

[lambda ind]=sort(lambda,'descend');%降序排列lambda

T=T(:,ind); % (fliplr)



%方差贡献率;

Xsum=sum(lambda);

rate=lambda/Xsum;



% 累计方差贡献率和主成分数

sumrate=0;

for m=1:p

  sumrate=sumrate+rate(m);

    if sumrate>0.85

      break

    end

end

m%取前几个主成分

结果：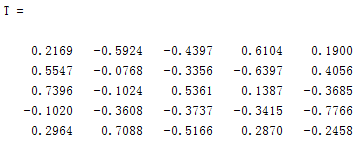

2，用matlab自带princecomp()函数计算

[coeff, score, latent2, tsquare] = princomp(A)

%A—原始数据或无量纲化后的数据，每一行是样品，每一列是变量（指标）

%coeff — 是p阶矩阵，每一列是主成分的系数向量，即特征值对应的标准正交向量

%score — 是p阶矩阵，每个元素都是主成分的得分，第一列是第一主成分，依此类推

%latent— 特征值，按从大到小的顺序排列的列向量

%tsquare — T统计量

        

结果：和我自己的T计算一致（后面三个系数不同是由于累积贡献率不同所致），score就是用主成分反表示X，latent2是特征值，tsquare是检验函数，没什么用。

 

这里补充说明：pcacov()函数.

在Matlab软件中，进行主成分分析的命令有两个，一个是直接对协方差矩阵进行计算，另一个是对无量纲化以后的数据矩阵进行计算.
[pc, latent, explained] = pcacov(X)
    X—（原始数据或无量纲化后的数据）的协方差矩阵
    pc — 每一列是主成分的系数向量，即特征值对应的标准正交向量
    latent— 特征值，按从大到小的顺序排列的列向量
    explained— 每个特征值的方差贡献率

[coeff, score, latent, tsquare] = princomp(X)
    X—原始数据或无量纲化后的数据，每一行是样品，每一列是变量（指标）
    coeff — 是p阶矩阵，每一列是主成分的系数向量，即特征值对应的标准正交向量
    score — 是p阶矩阵，每个元素都是主成分的得分，第一列是第一主成分，依此类推
    latent— 特征值，按从大到小的顺序排列的列向量
    tsquare — T统计量

 

这两个函数就是输入值不一样，其实可以明显发现：pcacov(cov(A))=princomp(A)%cov（）为求A的协方差函数

R语言：

   这里继续前文的法国经济数据做研究。

conomy

 

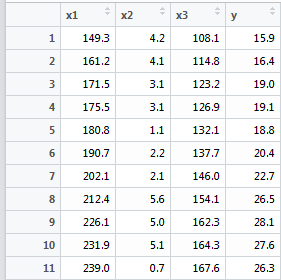
conomy.pr<-princomp(~x1+x2+x3, data=conomy, cor=T)//建立模型

summary(conomy.pr, loadings=TRUE)//观察

        

结果：staandard deviation表示标准擦，即aqrt（λ），proportion of variance表示主成分贡献率，Cumulative Proportion是累积贡献率。

而loadings是用主成分反表示X变量的系数，也可叫载重，在matlab中是score。我的理解就是新的主成分变量占原来变量的比重。

 

主成分分析后世

 

介绍完主成分分析，其实并没有结束，还有最后一步，用新得到的主成分去建立多远线性回归（降维后）。

pre<-predict(conomy.pr)

conomy$z1<-pre[,1]; conomy$z2<-pre[,2]

lm.sol<-lm(y~z1+z2, data=conomy)

summary(lm.sol)

                              

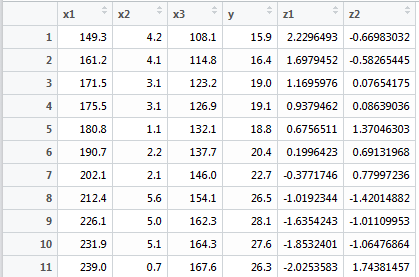
来解释一下Z1和Z2：

根据Z1计算的结果：

x1平均值	194.59	3.3	139.73
sd标准差	29.9999	1.6492	20.6344

再乘以主成分1的系数，正好就是-0.706*（149.3-194.59）/29.999-0.707*（108.1-139.73）/20.644=2.229.

依次类推，得到原响应变量和主成分的关系。

 

还有一步，可以进行，也可以不进行，就是通过主成分为媒介，建立yuan因变量和原自变量的关系（连乘系数即可，变回原坐标）

 

 最后补充两个主成分分析图：

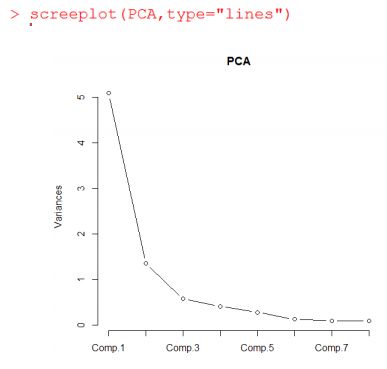
这叫碎石图（好逗逼的名字），横轴是主成分的个数，纵轴是特征值。有条虚线是随机数模拟计算出的特征值。此图用来确定主成分个数，特征值大于1的保留，最大拐点之上的保留。

这是bi图（名字忘了），是研究一对主成分对某个样本的关系，箭头长短代表着主成分矩阵系数的大小（我觉得没什么卵用）

 

 ps：以上数据和公式摘自薛毅《机器学习》一书，部分图像代码参考炼数成金课程ppt。