GitHub源码分享
项目主页: https://github.com/gozhuyinglong/blog-demos
本文源码: https://github.com/gozhuyinglong/blog-demos/tree/main/java-data-structures/src/main/java/com/github/gozhuyinglong/datastructures/linkedlist
1. 前言
通过前篇文章《数组》了解到数组的存储结构是一块连续的内存,插入和删除元素时其每个部分都有可能整体移动。为了避免这样的线性开销,我们需要保证数据可以不连续存储。本篇介绍另一种数据结构:链表。
2. 链表(Linked List)
链表是一种线性的数据结构,其物理存储结构是零散的,数据元素通过指针实现链表的逻辑顺序。链表由一系列结点(链表中每一个元素称为节点)组成,节点可以在内存中动态生成。
链表的特性:
- 链表是以节点(Node)的方式来存储,所以又叫链式存储。
- 节点可以连续存储,也可以不连续存储。
- 节点的逻辑顺序与物理顺序可以不一致
- 表可以扩充(不像数组那样还得重新分配内存空间)
链表分为单链表、双链表和环形链表,下面通过实例逐个介绍。
3. 单链表(Singly Linked List)
单链表又叫单向链表,其节点由两部分构成:
data域:数据域,用来存储元素数据next域:用于指向下一节点
单链表的结构如下图:
3.1 单链表的操作
单链表的所有操作都是从head开始,head本身不存储元素,其next指向第一个节点,然后顺着next链进行一步步操作。其尾部节点的next指向为空,这也是判断尾部节点的依据。
这里主要介绍插入和删除节点的操作。
3.1.1 插入节点
向单链表中插入一个新节点,可以通过调整两次next指向来完成。如下图所示,X为新节点,将其next指向为A2,再将A1的next指向为X即可。
若是从尾部节点插入,直接将尾部节点的next指向新节点即可。
3.1.2 删除节点
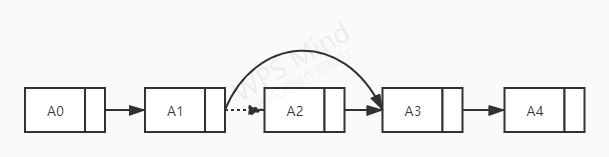
从单链表中删除一个节点,可以通过修改next指向来实现,如下图所示,将A1的next指向为A3,这样便删除A2,A2的内存空间会自动被垃圾回收。
若是删除尾部节点,直接将上一节点的next指向为空即可。
3.2 代码实现
我们使用Java代码来实现一个单链表。其中Node类存储单链表的一个节点,SinglyLinkedList类实现了单链表的所有操作方法。SinglyLinkedList类使用带头节点的方式实现,即head节点,该节点不存储数据,只是标记单链表的开始。
public class SinglyLinkedListDemo {
public static void main(String[] args) {
Node node1 = new Node(1, "张三");
Node node2 = new Node(3, "李四");
Node node3 = new Node(7, "王五");
Node node4 = new Node(5, "赵六");
SinglyLinkedList singlyLinkedList = new SinglyLinkedList();
System.out.println("-----------添加节点(尾部)");
singlyLinkedList.add(node1);
singlyLinkedList.add(node2);
singlyLinkedList.add(node3);
singlyLinkedList.add(node4);
singlyLinkedList.print();
System.out.println("-----------获取某个节点");
Node node = singlyLinkedList.get(3);
System.out.println(node);
singlyLinkedList.remove(node3);
System.out.println("-----------移除节点");
singlyLinkedList.print();
System.out.println("-----------修改节点");
singlyLinkedList.update(new Node(5, "赵六2"));
singlyLinkedList.print();
System.out.println("-----------按顺序添加节点");
Node node5 = new Node(4, "王朝");
singlyLinkedList.addOfOrder(node5);
singlyLinkedList.print();
}
private static class SinglyLinkedList {
// head节点是单链表的开始,不用来存储数据
private Node head = new Node(0, null);
/**
* 将节点添加到尾部
*
* @param node
*/
public void add(Node node) {
Node temp = head;
while (true) {
if (temp.next == null) {
temp.next = node;
break;
}
temp = temp.next;
}
}
/**
* 按顺序添加节点
*
* @param node
*/
public void addOfOrder(Node node) {
Node temp = head;
while (true) {
if (temp.next == null) {
temp.next = node;
break;
} else if(temp.next.key > node.getKey()){
node.next = temp.next;
temp.next = node;
break;
}
temp = temp.next;
}
}
/**
* 获取某个节点
*
* @param key
* @return
*/
public Node get(int key) {
if (head.next == null) {
return null;
}
Node temp = head.next;
while (temp != null) {
if (temp.key == key) {
return temp;
}
temp = temp.next;
}
return null;
}
/**
* 移除一个节点
*
* @param node
*/
public void remove(Node node) {
Node temp = head;
while (true) {
if (temp.next == null) {
break;
}
if (temp.next.key == node.key) {
temp.next = temp.next.next;
break;
}
temp = temp.next;
}
}
/**
* 修改一个节点
*
* @param node
*/
public void update(Node node) {
Node temp = head.next;
while (true) {
if (temp == null) {
break;
}
if (temp.key == node.key) {
temp.value = node.value;
break;
}
temp = temp.next;
}
}
/**
* 打印链表
*/
public void print() {
Node temp = head.next;
while (temp != null) {
System.out.println(temp.toString());
temp = temp.next;
}
}
}
private static class Node {
private final int key;
private String value;
private Node next;
public Node(int key, String value) {
this.key = key;
this.value = value;
}
public int getKey() {
return key;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public Node getNext() {
return next;
}
@Override
public String toString() {
return "Node{" +
"key=" + key +
", value='" + value + '\'' +
'}';
}
}
}输出结果:
-----------添加节点(尾部)
Node{key=1, value='张三'}
Node{key=3, value='李四'}
Node{key=7, value='王五'}
Node{key=5, value='赵六'}
-----------获取某个节点
Node{key=3, value='李四'}
-----------移除节点
Node{key=1, value='张三'}
Node{key=3, value='李四'}
Node{key=5, value='赵六'}
-----------修改节点
Node{key=1, value='张三'}
Node{key=3, value='李四'}
Node{key=5, value='赵六2'}
-----------按顺序添加节点
Node{key=1, value='张三'}
Node{key=3, value='李四'}
Node{key=4, value='王朝'}
Node{key=5, value='赵六2'}3.3 单链表的缺点
通过对单链表的分析,可以看出单链表有如下缺点:
(1)单链表的查找方法只能是一个方向
(2)单链表不能自我删除,需要靠上一节点进行辅助操作。
而这些缺点可以通过双链表来解决,下面来看详细介绍。
4. 双链表(Doubly Linked List)
双链表又叫双向链表,其节点由三部分构成:
prev域:用于指向上一节点data域:数据域,用来存储元素数据next域:用于指向下一节点
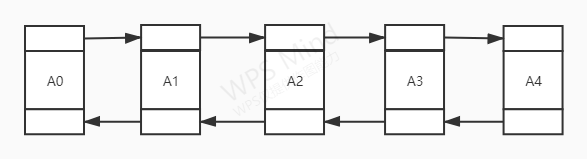
双链表的结构如下图:
4.1 双链表的操作
双链表的操作可以从两端开始,从第一个节点通过next指向可以一步步操作到尾部,从最后一个节点通过prev指向可以一步步操作到头部。
这里主要介绍插入和删除节点的操作。
4.1.1 插入节点
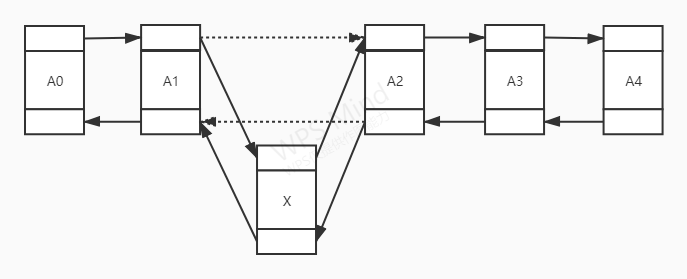
向双链表中插入一个新节点,需要通过调整两次prev指向和两次next指向来完成。如下图所示,X为新节点,将A1的next指向X,将X的next指向A2,将A2的prev指向X,将X的prev指向A1即可。
4.1.2 删除节点
从双链表中删除一个节点,需要通过调整一次prev指向和一次next指向来完成。如下图所示,删除A2节点,将A1的next指向A3,将A3的 prev指向A1即可。
4.2 代码实现
我们使用Java代码来实现一个双链表。其中 Node类存储双链表的一个节点,DoublyLinkedListDemo类实现双链表的所有操作方法。DoublyLinkedListDemo类使用不带头节点的方式实现,其中first为第一个节点,last为最后一个节点。这两个节点默认都为空,若只有一个元素时,则两个节点指向同一元素。
public class DoublyLinkedListDemo {
public static void main(String[] args) {
DoublyLinkedList doublyLinkedList = new DoublyLinkedList();
System.out.println("-----------从尾部添加节点");
doublyLinkedList
.addToTail(new Node(1, "张三"))
.addToTail(new Node(3, "李四"))
.addToTail(new Node(7, "王五"))
.addToTail(new Node(5, "赵六"))
.print();
System.out.println("-----------从头部添加节点");
doublyLinkedList
.addToHead(new Node(0, "朱开山"))
.print();
System.out.println("-----------获取某个节点");
System.out.println(doublyLinkedList.get(3));
System.out.println("-----------移除节点");
doublyLinkedList
.remove(new Node(3, "李四"))
.print();
System.out.println("-----------修改节点");
doublyLinkedList
.update(new Node(5, "赵六2")).print();
System.out.println("-----------按顺序添加节点");
doublyLinkedList
.addOfOrder(new Node(4, "王朝"))
.print();
}
private static class DoublyLinkedList {
private Node first = null; // first节点是双链表的头部,即第一个节点
private Node last = null; // tail节点是双链表的尾部,即最后一个节点
/**
* 从尾部添加
*
* @param node
*/
public DoublyLinkedList addToTail(Node node) {
if (last == null) {
first = node;
} else {
last.next = node;
node.prev = last;
}
last = node;
return this;
}
/**
* 按照顺序添加
*
* @param node
*/
public DoublyLinkedList addOfOrder(Node node) {
if (first == null) {
first = node;
last = node;
return this;
}
// node比头节点小,将node设为头节点
if (first.key > node.key) {
first.prev = node;
node.next = first;
first = node;
return this;
}
// node比尾节点大,将node设为尾节点
if (last.key < node.key) {
last.next = node;
node.prev = last;
last = node;
return this;
}
Node temp = first.next;
while (true) {
if (temp.key > node.key) {
node.next = temp;
node.prev = temp.prev;
temp.prev.next = node;
temp.prev = node;
break;
}
temp = temp.next;
}
return this;
}
/**
* 从头部添加
*
* @param node
*/
public DoublyLinkedList addToHead(Node node) {
if (first == null) {
last = node;
} else {
node.next = first;
first.prev = node;
}
first = node;
return this;
}
/**
* 获取节点
*
* @param key
* @return
*/
public Node get(int key) {
if (first == null) {
return null;
}
Node temp = first;
while (temp != null) {
if (temp.key == key) {
return temp;
}
temp = temp.next;
}
return null;
}
/**
* 移除节点
*
* @param node
*/
public DoublyLinkedList remove(Node node) {
if (first == null) {
return this;
}
// 要移除的是头节点
if (first == node) {
first.next.prev = null;
first = first.next;
return this;
}
// 要移除的是尾节点
if (last == node) {
last.prev.next = null;
last = last.prev;
return this;
}
Node temp = first.next;
while (temp != null) {
if (temp.key == node.key) {
temp.prev.next = temp.next;
temp.next.prev = temp.prev;
break;
}
temp = temp.next;
}
return this;
}
/**
* 修改某个节点
*
* @param node
*/
public DoublyLinkedList update(Node node) {
if (first == null) {
return this;
}
Node temp = first;
while (temp != null) {
if (temp.key == node.key) {
temp.value = node.value;
break;
}
temp = temp.next;
}
return this;
}
/**
* 打印链表
*/
public void print() {
if (first == null) {
return;
}
Node temp = first;
while (temp != null) {
System.out.println(temp);
temp = temp.next;
}
}
}
private static class Node {
private final int key;
private String value;
private Node prev; // 指向上一节点
private Node next; // 指向下一节点
public Node(int key, String value) {
this.key = key;
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"key=" + key +
", value='" + value + '\'' +
'}';
}
}
}输出结果:
-----------从尾部添加节点
Node{key=1, value='张三'}
Node{key=3, value='李四'}
Node{key=7, value='王五'}
Node{key=5, value='赵六'}
-----------从头部添加节点
Node{key=0, value='朱开山'}
Node{key=1, value='张三'}
Node{key=3, value='李四'}
Node{key=7, value='王五'}
Node{key=5, value='赵六'}
-----------获取某个节点
Node{key=3, value='李四'}
-----------移除节点
Node{key=0, value='朱开山'}
Node{key=1, value='张三'}
Node{key=7, value='王五'}
Node{key=5, value='赵六'}
-----------修改节点
Node{key=0, value='朱开山'}
Node{key=1, value='张三'}
Node{key=7, value='王五'}
Node{key=5, value='赵六2'}
-----------按顺序添加节点
Node{key=0, value='朱开山'}
Node{key=1, value='张三'}
Node{key=4, value='王朝'}
Node{key=7, value='王五'}
Node{key=5, value='赵六2'}5. 环形链表(Circular Linked List)
环形链表又叫循环链表,本文讲述的是环形单向链表,其与单链表的唯一区别是尾部节点的next不再为空,则是指向了头部节点,这样便形成了一个环。
环形链表的结构如下图:
5.1 约瑟夫问题
约瑟夫问题:有时也称为约瑟夫斯置换,是一个计算机科学和数学中的问题。在计算机编程的算法中,类似问题又称为约瑟夫环。又称“丢手绢问题”。
引自百度百科:
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第 k个人。接着,再越过k-1个人,并杀掉第 k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15 个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。
问题分析与算法设计
约瑟夫问题并不难,但求解的方法很多;题目的变化形式也很多。这里给出一种实现方法。
题目中30个人围成一圈,因而启发我们用一个循环的链来表示,可以使用结构数组来构成一个循环链。结构中有两个成员,其一为指向下一个人的指针,以构成环形的链;其二为该人是否被扔下海的标记,为1表示还在船上。从第一个人开始对还未扔下海的人进行计数,每数到9时,将结构中的标记改为0,表示该人已被扔下海了。这样循环计数直到有15个人被扔下海为止。
5.2 代码实现
我们使用Java代码来实现一个环形链表,并将节点按约瑟夫问题顺序出列。
public class CircularLinkedListDemo {
public static void main(String[] args) {
CircularLinkedList circularLinkedList = new CircularLinkedList();
System.out.println("-----------添加10个节点");
for (int i = 1; i <= 10; i++) {
circularLinkedList.add(new Node(i));
}
circularLinkedList.print();
System.out.println("-----------按约瑟夫问题顺序出列");
circularLinkedList.josephusProblem(3);
}
private static class CircularLinkedList {
private Node first = null; // 头部节点,即第一个节点
/**
* 添加节点,并将新添加的节点的next指向头部,形成一个环形
*
* @param node
* @return
*/
public void add(Node node) {
if (first == null) {
first = node;
first.next = first;
return;
}
Node temp = first;
while (true) {
if (temp.next == null || temp.next == first) {
temp.next = node;
node.next = first;
break;
}
temp = temp.next;
}
}
/**
* 按约瑟夫问题顺序出列
* 即从第1个元素开始报数,报到num时当前元素出列,然后重新从下一个元素开始报数,直至所有元素出列
*
* @param num 表示报几次数
*/
public void josephusProblem(int num) {
Node currentNode = first;
// 将当前节点指向最后一个节点
do {
currentNode = currentNode.next;
} while (currentNode.next != first);
// 开始出列
while (true) {
// 当前节点要指向待出列节点的前一节点(双向环形队列不需要)
for (int i = 0; i < num - 1; i++) {
currentNode = currentNode.next;
}
System.out.printf("%s\t", currentNode.next.no);
if(currentNode.next == currentNode){
break;
}
currentNode.next = currentNode.next.next;
}
}
/**
* 输出节点
*/
public void print() {
if (first == null) {
return;
}
Node temp = first;
while (true) {
System.out.printf("%s\t", temp.no);
if (temp.next == first) {
break;
}
temp = temp.next;
}
System.out.println();
}
}
private static class Node {
private final int no;
private Node next; // 指向下一节点
public Node(int no) {
this.no = no;
}
@Override
public String toString() {
return "Node{" +
"no=" + no +
'}';
}
}
}输出结果:
-----------添加10个节点
1 2 3 4 5 6 7 8 9 10
-----------按约瑟夫问题顺序出列
3 6 9 2 7 1 8 5 10 4