对称加密(2) 对称加密算法
对称加密(2) 对称加密算法
经典的对称加密算法是DES算法,后来又衍生出3DES、TripleDES等增强型的DES算法。此外,.NET还提供了RC2、Rijndael等对称加密算法。下面分别详细介绍。
DES加密算法
对称加密算法中最经典的算法莫过于DES加密算法。DES加密采用的是分组加密的方法,使用56位密钥加密64位明文,最后产生64位密文。DES算法的基本流程如图6-2所示。
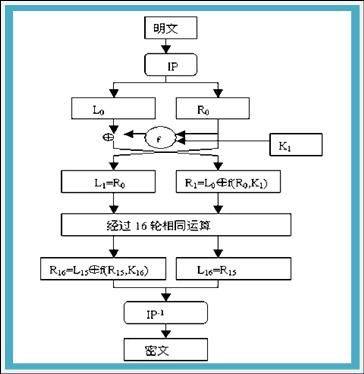
图6-2 DES加密算法基本流程
现在对图6-2的整个流程做简要的分析。DES对64位的明文分组M进行操作,M经过一个初始置换IP置换成m0,将m0明文分成左半部分和右半部分m0=(L0,R0),各32位长。然后进行16轮完全相同的运算,这些运算称为函数f,在运算过程中,数据与密匙结合。经过16轮运算之后,可以看到第16轮运算,将右侧第15轮运算的结果(R15)作为左侧运算的最终结果(L16),而右侧最后的结果(R16)为左侧第15轮运算结果(L15)和函数f运算结果的异或运算所得。此后,再将左、右部分合在一起经过一个逆置换,输出密文。
实际加密过程要分成两个同时进行的过程,即加密过程和密钥生成过程,如图6-3所示。结合图6-2和图6-3简单讲解密钥生成过程。

图6-3 加密与密钥生成
如图6-3所示,在16轮循环的每一轮中,密匙位移位,然后再从密匙的64位中选出48位。通过一个扩展置换将数据的右半部分扩展成48位,并通过一个异或操作替代成新的32位数据,在将其置换一次。这四步运算构成了图6-2中的函数f。然后,通过另一个异或运算,函数f的输出与左半部分结合,其结果成为新的右半部分,原来的右半部分成为新的左半部分。该操作重复16次。
DES算法的解密过程和加密过程几乎完全相同,只是使用密钥的顺序相反。
关于DES算法的更加详细的细节不在本书的讲解范围之内,请读者参考相关资料。
NIST(National Institute of Standards and Technology,美国国家标准技术研究院)在1999年发布了新的DES加密标准,3DES取代DES成为新的加密标准。3DES采用168位的密钥,三重加密,但速度较慢。之后,又出现了AES(Advanced Encryption Standard,先进加密标准)等高级对称机密算法。
TripleDES加密算法
由于DES算法安全性方面的原因,为了提高DES算法的抗攻击性,因此提出了Triple-DES算法。
Triple-DES算法的基本原理是:用两个密钥对数据进行3次加密/解密运算。即首先使用第一个密钥对数据进行加密,然后用第二个密钥对其进行解密,最后用第一个密钥再加密。这两个密钥可以是同一个,也可以不同,它们也可以来源于一个128位密钥,只是在加密/解密时将其分割成两个64位的密钥,分别轮换使用这两个64位密钥去完成加密/解密运算。Triple-DES算法保留了DES算法运算速度快的特点,通过增加运算次数和密钥长度(两个64位密钥相当于128位密钥)来增加破解者的破解时间,但是从密码学本身来说,其安全强度并没有增加。
RC系列算法
现在我们用到的RC系列算法包括RC2、RC4、RC5、RC6算法,其中RC4是序列密码算法,其他三种是分组密码算法。
(1) RC2算法
该算法设计的目的是用来取代DES算法,它采用密钥长度可变的对明文采取64位分组的分组加密算法,属于Festel网络结构。
(2) RC4算法
该算法是一个密钥长度可变的面向字节流的加密算法,以随机置换为基础。该算法执行速度快,每输出1字节的结果仅需要8~16字节的机器指令。RC4算法比较容易描述,它首先用8~2048位可变长度的密钥初始化一个256字节的状态矢量S。S的成员标记为S[0],S[1],…,S[255],整个置换过程都包含0~255的8比特数。对于加密和解密,设字节数据为K,由S中256个元素按一定方式选出一个元素生成,每生成一个K值,元素中的数据就要被重新置换一次。RC4初始化的伪代码如代码清单6-1所示。
代码清单6-1 RC4初始化的伪代码
for i=0 to 255
{
S[i]=i;
T[i]=K[i mod KeyLen ];
}
j=0;
for i=0 to 255
{
j=(j+T[i]+S[i]) mod 256;
swap(S[i],S[j];
}
如代码清单6-1所示,初始化开始时,S的元素按从0到255依次赋值,同时建立一个临时矢量T。如果密钥K的长度为256字节,则将K赋值给T。否则,若密钥长度为KeyLen字节,则将K的值赋给T的前KeyLen个元素,并循环重复用K余下的元素赋给T剩下的元素。从“j=0”开始,用T产生S的初始置换。从S[0]~S[255],对每个S[i]根据T[i]确定的方案,将S[i]置换成S中的另一字节。
在完成S的初始化之后,输入密钥将被抛弃,接下来将使用密钥流,生成密钥流的伪代码如代码清单6-2所示。
代码清单6-2 生成密钥流
i=0;
j=0;
while(true)
{
i=(i+1) mod 256;
j=(j+S[i]) mod 256;
swap(S[i],j[i];
T=(S[i]+S[j]) mod 256;
K=S[T];
}
如代码清单6-2所示,密钥流的生成是从S[0]到S[255],对每个S[i]根据当前S的值将S[i]与S中的另一字节替换,当S[255]完成置换后操作继续重复。在加密过程中将K的值与下一明文字节异或,解密过程中将K的值与下一密文字节异或即可。
(3) RC5算法
该算法是一种分组长度、密钥长度、加密迭代轮数都可变的分组加密算法。该算法主要包含三部分内容:密钥扩展、加密算法和解密算法。该算法包含三个参数:w(字的长度,单位:位)、r(迭代次数)、b(密钥长度,单位:字节)。由于RC5算法需要(2r+2)个w位密钥,所以需要密钥扩展。
通过密钥扩展,把密钥K扩展成密钥阵S,它由K所决定的t=2(r+1)个随机二进制字构成。密钥扩展算法利用了两个幻常数:
函数Odd(x)的结果为与x最近的奇整数。密钥扩展的第一步是将密钥K转换成字格式,利用K的各字节构造字阵L。密钥扩展的第二步是利用模232线性同余算法初始化S阵。密钥扩展的第三步是L阵和S阵混合。
加密过程也很简单。假设选用的数据分组长度为2w位(w允许的值有16、32和64),迭代次数为r轮(r为0~255)。首先将明文划分成两个w位的字A和B,运算过程如代码清单6-3所示。
代码清单6-3 RC5算法加密过程
A=A+S0;
B=B+S1;
for i=1 to r
{
A=((A+B)<<<B))+S2i;
B= ((B+A) <<<A)) +S2i+1;
}
代码清单6-3的结果输出到寄存器A和B中。
解密过程是加密过程的逆运算,基本过程如代码清单6-4所示。
代码清单6-4 RC5算法解密过程
for i=r down to 1
{
B=((B- S2i+1)>>>A)+A;
A=((A- S2i)>>>B)+B;
}
B=B-S1;
A=A-S0;
说明 加密和解密过程中的加减都是模2w的,表示逐位异或。<<<表示循环左移,>>>表示循环右移。
(4) RC6算法
RC6秉承了RC5设计简单、广泛使用数据相关的循环移位思想,同时增强了抵抗攻击的能力,改进了RC5中循环移位的位数依赖于寄存器中所有位的不足。
RC6的特点是输入的明文由原先2个区块扩展为4个区块,另外,在运算方面则是使用了整数乘法,而整数乘法的使用则在每一个运算回合中增加了扩散(diffusion)的行为,并且使得即使很少的回合数也有很高的安全性。同时,RC6中所用的操作可以在大部分处理器上高效率地实现,提高了加密速度。RC6是一种安全、架构完整而且简单的区块加密法。它提供了较好的测试结果和参数方面相当大的弹性。RC6可以抵抗所有已知的攻击,能够提供AES所要求的安全性,可以说是近几年来相当优秀的一种加密法。
Rijndael算法
Rijndael是一个反复运算的加密算法,它允许可变动的数据区块及密钥的长度。数据区块与密钥长度的变动是各自独立的。
在Rijndael算法中定义了两个名词:
1) State:在运算过程中所产生的中间值,是一个4×Nb的矩阵,Nb可由数据长度除以32位求得,也就是把数据分割成Nb个区块。
2) Cipher Key:用来做加密运算的密钥,形式是一个4×Nk的矩阵,Nk可由金钥长度除以32位求得,也就是把密钥分割成Nk个32位的子密钥。
在Rijndael算法中,运算的回合数(Nr)是由Nb及Nk决定的,回合数的变动定义如表6-1所示。
表6-1 Rijndael算法回合变动定义
| Nr |
Nb=4 |
Nb=6 |
Nb=8 |
| Nk=4 |
10 |
12 |
14 |
| Nk=6 |
12 |
12 |
14 |
| Nk=8 |
14 |
14 |
14 |
在Rijndael中使用了许多字节层级的运算,而这些运算是以GF(28)为基础架构。也有一些采用了4-byte的字组运算。各种运算的定义如下:
(1) GF(28)的定义
假设一个字节b由b7b6b5b4b3b2b1b0组成,可以把这些bi想象成一个7次多项式的系数,而这些系数不是0就是1:
b7 x7+ b6 x6+ b5 x5+ b4 x4+ b3 x3+ b2 x2+ b1 x + b0
例如,(57)16的二进制表示法为(0101,0111)2,表示成多项式,则为:
x6+ x4+ x2+ x + 1
(2)加法
两个多项式的加法,则是定义为相同指数项的系数和再模2,简单地说,就是作EXOR运算(1+1=0)。例如:
(57)16+(83)16=(01010111)2+(10000011)2 = (11010100)2 = (D4)16
或是
(x6+x4+x2+x+1)+(x7+x+1)=x7+x6+x4+x2
(3)乘法
在乘法运算中,多项式相乘之后的结果很容易造成溢位的问题,解决溢位的方式是把相乘的结果,再模余一个不可分解的多项式m(x)。在Rijndael中,定义一个这样的多项式为m(x)=x8+x4+x3+x+1或是(11B)16例如:
(57)16‧(83)16
=(x6+ x4+ x2+ x + 1)‧(x7+ x + 1)
=x13+ x11+ x9+ x8+ x7+x7+ x5+ x3+ x2+x+x6+ x4+ x2+ x + 1
=(x13+x11+x9+x8+x6+x5+x4+x3+1+x13+x11+x9+x8+x6+x5+x4+x3+1)mod(x8+x4+x3+x+1)
= x7+ x6+ 1
=(C1)16
(4)乘以x
若把b(x)乘以x,得到
b7 x8+ b6 x7+ b5 x6+ b4 x5+ b3 x4+ b2 x3+ b1 x2 + b0x
若b7=0,不会发生溢位问题,答案即是正确的;若b7=1,发生溢位问题,必须减去m(x)。可以把这种运算表示为xtime(x),其运算方式为left shift(若溢位则和(1B)16做EXOR运算),例如:
‘57’· ‘13’ = ‘FE’
‘57’ · ‘02’ = xtime(57) = ‘AE’
‘57’ · ‘04’ = xtime(AE) = ‘47’
‘57’ · ‘08’ = xtime(47) = ‘8E’
‘57’ · ‘10’ = xtime(8E) = ‘07’
‘57’ · ‘13’ = ‘57’ · (‘01’⊕‘02’⊕‘10’) = ‘57’⊕‘AE’⊕‘07’ = ‘FE’
Rijndael算法分为四个步骤:
步骤 1 字节转换。
字节转换是一个以字节为单位的非线性取代运算,取代表(S-box)是经过2个运算过程而建立,并且是可逆的。首先找出每个字节在GF(28)中的乘法反元素;接着经过1个仿射(Affine)转换运算,转换运算的定义如图6-4所示。

图6-4 转换运算定义
取代表生成之后就可以进行字节取代运算。取代运算的示意图如图6-5所示。
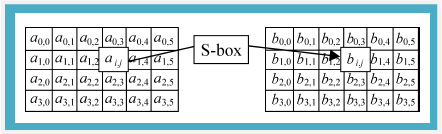
图6-5 取代运算示意图
进行如图6-5的取代运算之后,结果如图6-6所示。
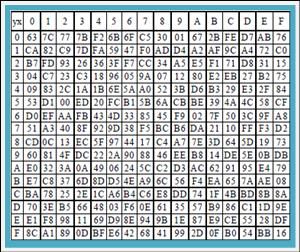
图6-6 取代运算后的S-Box
说明 字节取代转换的反运算:计算仿射对应之后的相反运算可得到S-1-box,以此S-1-box做字节取代(Subbytes)即可。
步骤 2 移行转换。
在这个转换中,State的每一行以不同的偏移量做环状位移:第0 行不动,第1 行位移1 C个字节,第2 行位移2 C个字节,第3 行位移3 C个字节。位移的偏移量C1,C2,C3跟区块的数目(Nb)有关,关系见图6-7。
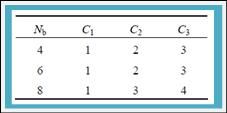
图6-7 C1、 C2、 C3与区块数目(Nb)的关系
移行转换(Shift rows)运算对于State 的影响如图6-8所示。

图6-8 移行转换对State的影响
说明 移行转换的反运算:对第2、第3 及第4 行做Nb-C1、、Nb-C2、Nb-C3个字节的环状位移即可。
步骤 3 混列转换。
在这个转换中,把State当做一个GF(28)中的多项式。并且对一个固定的多项式c(x)作乘法,如果发生溢位,则再模x4 +1. 表示如下:
c(x) ='03' x3 +'01' x2 +'01' x +'02'
c(x)与x4 +1互质,令
b(x) = c(x)⊕ a(x)
以矩阵乘法表示如图6-9所示。

图6-9 混列转换的矩阵乘法表示
State经过混列(Mix columns)运算之后的变化如图6-9所示。
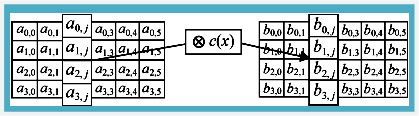
图6-9 混列运算对State的影响
说明 混列转换的反运算是乘以一个特殊的多项式d(x):
('03' x3 +'01' x2 +'01' x +'02' )⊕ d(x)
='01' d(x)
='0B' x3 +'0D' x2 +'09' x +'0E'。
步骤 4 轮密钥加。
这个运算主要是把每一个回合密钥(Roundkey)透过简单的Bitwise exor加入到每一个State中,如图6-10所示。
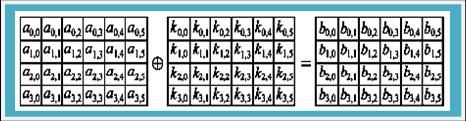
图6-10 Bitwise exor加入后的State
说明 此时Add round key的逆是它自身。