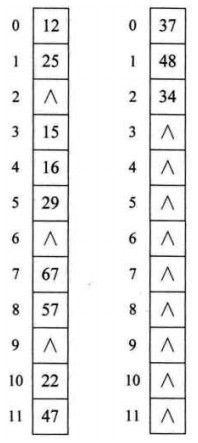
处理散列冲突的方法
1. 开放定址法
开放定址法就是一旦发生冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入。
Hi = (H(key) + di) MOD m, i=1,2,…, k(k<=m-1),其中H(key)为散列函数,m为散列表长,di为增量序列。di可有下列三种取法:
(1)di=1,2,3,…, m-1,称为线性探测再散列;
(2)di=1^2, -(1^2), 2^2, -(2^2), 3^2, …, ±(k^2),(k<=m/2),称二为次探测再散列;
(3)di=伪随机数序列,称为伪随机探测再散列。
所谓伪随机数,用同样的随机种子,将得到相同的数列。
2. 再散列函数法
Hi=RHi(key), i=1,2,…,k RHi均是不同的散列函数(比如除留余数、折叠、平方取中),在同义词产生地址冲突时就换用另一个散列函数计算散列地址,直到碰撞不再发生,这种方法不易产生“聚集”,但增加了计算时间。
3. 链地址法
将所有关键字为同义词的记录存储在一个单链表中,称这种表为同义词子表,在散列表中只存储所有同义词子表的头指针。
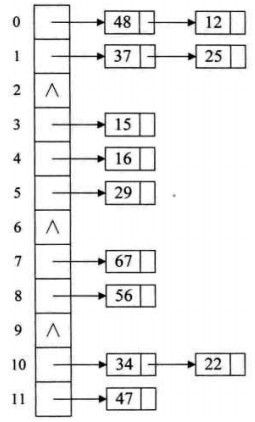
链地址法对于可能会造成很多冲突散列函数来说,提供了绝不会出现找不到地址的保障。但也就带来了查找时需要遍历单链表的性能损耗。
4. 公共溢出区法
为所有冲突的关键字记录建立一个公共的溢出区来存放。在查找时,对给定关键字通过散列函数计算出散列地址后,先与基本表的相应位置进行比对,如果相等,则查找成功;如果不相等,则到溢出表进行顺序查找。如果相对于基本表而言,在有冲突的数据很少的情况下,公共溢出区的结构对查找性能来说还是非常高的。