哈夫曼树与哈夫曼编码

在一般的数据结构的书中，树的那章后面，著者一般都会介绍一下哈夫曼(HUFFMAN)

树和哈夫曼编码。哈夫曼编码是哈夫曼树的一个应用。哈夫曼编码应用广泛，如

JPEG中就应用了哈夫曼编码。 首先介绍什么是哈夫曼树。哈夫曼树又称最优二叉树，

是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点

的权值乘上其到根结点的 路径长度（若根结点为0层，叶结点到根结点的路径长度

为叶结点的层数）。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+...+Wn*Ln)

，N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树，相应的叶结点的路径

长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。

哈夫曼编码步骤：

一、对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算 法，一般还要求以Ti的权值Wi的升序排列。）
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步，直到集合F中只有一棵二叉树为止。

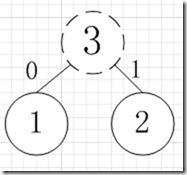
简易的理解就是，假如我有A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树，即取1，2构成新树，其结点为1+2=3，如图：

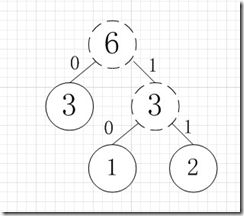
虚线为新生成的结点，第二步再把新生成的权值为3的结点放到剩下的集合中，所以集合变成{5,4,3,3}，再根据第二步，取最小的两个权值构成新树，如图：

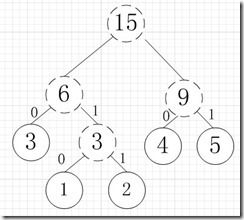
再依次建立哈夫曼树，如下图：

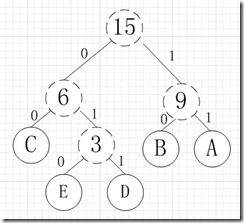
其中各个权值替换对应的字符即为下图：

所以各字符对应的编码为：A->11,B->10,C->00,D->011,E->010

霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩，加密解密等场合。

 

C语言代码实现：

/*-------------------------------------------------------------------------

 * Name:   哈夫曼编码源代码。

 * Date:   2011.04.16

 * Author: Jeffrey Hill+Jezze(解码部分)

 * 在 Win-TC 下测试通过

 * 实现过程：着先通过 HuffmanTree() 函数构造哈夫曼树，然后在主函数 main()中

 *           自底向上开始(也就是从数组序号为零的结点开始)向上层层判断，若在

 *           父结点左侧，则置码为 0,若在右侧,则置码为 1。最后输出生成的编码。

 *------------------------------------------------------------------------*/

#include <stdio.h>

#include<stdlib.h>

#define MAXBIT      100

#define MAXVALUE  10000

#define MAXLEAF     30

#define MAXNODE    MAXLEAF*2 -1

typedef struct 

{

    int bit[MAXBIT];

    int start;

} HCodeType;        /* 编码结构体 */

typedef struct

{

    int weight;

    int parent;

    int lchild;

    int rchild;

    int value;

} HNodeType;        /* 结点结构体 */

/* 构造一颗哈夫曼树 */

void HuffmanTree (HNodeType HuffNode[MAXNODE],  int n)

{ 

    /* i、j： 循环变量，m1、m2：构造哈夫曼树不同过程中两个最小权值结点的权值，

        x1、x2：构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/

    int i, j, m1, m2, x1, x2;

    /* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */

    for (i=0; i<2*n-1; i++)

    {

        HuffNode[i].weight = 0;//权值 

        HuffNode[i].parent =-1;

        HuffNode[i].lchild =-1;

        HuffNode[i].rchild =-1;

        HuffNode[i].value=i; //实际值，可根据情况替换为字母  

    } /* end for */

    /* 输入 n 个叶子结点的权值 */

    for (i=0; i<n; i++)

    {

        printf ("Please input weight of leaf node %d: \n", i);

        scanf ("%d", &HuffNode[i].weight);

    } /* end for */

    /* 循环构造 Huffman 树 */

    for (i=0; i<n-1; i++)

    {

        m1=m2=MAXVALUE;     /* m1、m2中存放两个无父结点且结点权值最小的两个结点 */

        x1=x2=0;

        /* 找出所有结点中权值最小、无父结点的两个结点，并合并之为一颗二叉树 */

        for (j=0; j<n+i; j++)

        {

            if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1)

            {

                m2=m1; 

                x2=x1; 

                m1=HuffNode[j].weight;

                x1=j;

            }

            else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)

            {

                m2=HuffNode[j].weight;

                x2=j;

            }

        } /* end for */

            /* 设置找到的两个子结点 x1、x2 的父结点信息 */

        HuffNode[x1].parent  = n+i;

        HuffNode[x2].parent  = n+i;

        HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;

        HuffNode[n+i].lchild = x1;

        HuffNode[n+i].rchild = x2;

        printf ("x1.weight and x2.weight in round %d: %d, %d\n", i+1, HuffNode[x1].weight, HuffNode[x2].weight);  /* 用于测试 */

        printf ("\n");

    } /* end for */

  /*  for(i=0;i<n+2;i++)

    {

        printf(" Parents:%d,lchild:%d,rchild:%d,value:%d,weight:%d\n",HuffNode[i].parent,HuffNode[i].lchild,HuffNode[i].rchild,HuffNode[i].value,HuffNode[i].weight);

                  }*///测试 

} /* end HuffmanTree */

//解码 

void decodeing(char string[],HNodeType Buf[],int Num)

{

  int i,tmp=0,code[1024];

  int m=2*Num-1;

  char *nump;

  char num[1024];

  for(i=0;i<strlen(string);i++)

  {

   if(string[i]=='0')

  num[i]=0;        

  else

  num[i]=1;                    

  } 

  i=0;

  nump=&num[0];

 while(nump<(&num[strlen(string)]))

 {tmp=m-1;

  while((Buf[tmp].lchild!=-1)&&(Buf[tmp].rchild!=-1))

  {

   if(*nump==0)

   {

     tmp=Buf[tmp].lchild ;          

   } 

   else tmp=Buf[tmp].rchild;

   nump++;

  } 

  printf("%d",Buf[tmp].value);                                  

 }

}

int main(void)

{

    HNodeType HuffNode[MAXNODE];            /* 定义一个结点结构体数组 */

    HCodeType HuffCode[MAXLEAF],  cd;       /* 定义一个编码结构体数组， 同时定义一个临时变量来存放求解编码时的信息 */

    int i, j, c, p, n;

    char pp[100];

    printf ("Please input n:\n");

    scanf ("%d", &n);

    HuffmanTree (HuffNode, n);

    for (i=0; i < n; i++)

    {

        cd.start = n-1;

        c = i;

        p = HuffNode[c].parent;

        while (p != -1)   /* 父结点存在 */

        {

            if (HuffNode[p].lchild == c)

                cd.bit[cd.start] = 0;

            else

                cd.bit[cd.start] = 1;

            cd.start--;        /* 求编码的低一位 */

            c=p;                    

            p=HuffNode[c].parent;    /* 设置下一循环条件 */

        } /* end while */

        /* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */

        for (j=cd.start+1; j<n; j++)

        { HuffCode[i].bit[j] = cd.bit[j];}

        HuffCode[i].start = cd.start;

    } /* end for */

    /* 输出已保存好的所有存在编码的哈夫曼编码 */

    for (i=0; i<n; i++)

    {

        printf ("%d 's Huffman code is: ", i);

        for (j=HuffCode[i].start+1; j < n; j++)

        {

            printf ("%d", HuffCode[i].bit[j]);

        }

        printf(" start:%d",HuffCode[i].start);

        printf ("\n");

    }

/*    for(i=0;i<n;i++){

    for(j=0;j<n;j++)

        {

             printf ("%d", HuffCode[i].bit[j]);           

        }

        printf("\n");

        }*/

    printf("Decoding?Please Enter code:\n");

    scanf("%s",&pp);

decodeing(pp,HuffNode,n);

    getch();

    return 0;

}