Integer类的toBinaryString源码分析

jdk1.8( jdk11代码有所不同)  的Integer包装类中提供了已经封装好的进制转换函数  toBinaryString(),  toOctalString(), toHexString(),下面分析一下它们的源码。

//转二进制
public static String toBinaryString(int i) {
        return toUnsignedString0(i, 1);
}
//转八进制
public static String toOctalString(int i) {
        return toUnsignedString0(i, 3);
}
//转十六进制
public static String toHexString(int i) {
        return toUnsignedString0(i, 4);
}

从以上源码可以看出，它们都调用了toUnsignedString0()这个函数，只是第二个参数shift的值不同. 

1.  toUnsignedString()

接下来我们看看 toUnsignedString()是怎么实现的. 

 private static String toUnsignedString0(int val, int shift) {
        // assert shift > 0 && shift <=5 : "Illegal shift value";
        // 第一步: 计算出用于表示二/八/十六进制的字符数组的长度,并创建字符数组.
        int mag = Integer.SIZE - Integer.numberOfLeadingZeros(val);
        int chars = Math.max(((mag + (shift - 1)) / shift), 1);
        char[] buf = new char[chars];
        //第二步 使用formatUnsignedInt方法填充字符数组，得到所需进制表示的字符串并返回
        formatUnsignedInt(val, shift, buf, 0, chars);
        return new String(buf, true);
}

    第一步中最关键的字符数组长度的计算是通过numberOfLeadingZeros()方法计算int变量的计算机二进制表示的高位连续0位的数量，进而获得最高非0位到最低位的长度，也就是需要表示的位数, 负数的最高位是1。例如整数18在计算机中的二进制存储为0000，0000，0000，0000，0000，0000，0001，0010，那么需要表示的部分便是1，0010，前面的28位均为0，不用表示。而-18在计算机中的二进制存储为 11111111111111111111111111101110， 都须要表示. 

2.  numberOfLeadingZeros()

   这个函数一般给出的解决方案是通过判断高位是否为0，然后移位重复判断，记录连续的0的个数。如下列代码:

 public static int numberOfLeadingZeros0(int i){
        if(i == 0) {
            return 32;  // i为0,则32位全为0
        }
        int n = 0;
        int mask = 0x80000000;   // 即   1000 0000 0000 0000 0000 0000 0000 0000
        int j = i & mask;    //取出符号位，如符号位为 1,表示负数，则直接返回n=0.
        //从高位向低位搜索连续出现的0的个数
        while(j == 0){
            n++;         // 计数0出现的次数
            i <<= 1;     // <<表示左移移位，不分正负数，低位补0 
            j = i & mask;    // 取出左移后最高位的值。
        }
        return n;
}

以上方法的平均时间复杂度是o(k)，k为变量i的位数，如果i为int，k就是32。这种很基本的库函数会经过很多次的调用，需要进一步的优化. 

java源码中的写法更加优秀: 

//求从高位向低，连续出现的0的个数
public static int numberOfLeadingZeros(int i) {
        if (i == 0)
            return 32;
        int n = 1;
        // >>>表示无符号右移，也叫逻辑右移，即若该数为正，则高位补0，而若该数为负数，则右移后高位同样补0
        if (i >>> 16 == 0) { n += 16; i <<= 16; }  // <<表示左移移，不分正负数，低位补0
        if (i >>> 24 == 0) { n +=  8; i <<=  8; }
        if (i >>> 28 == 0) { n +=  4; i <<=  4; }
        if (i >>> 30 == 0) { n +=  2; i <<=  2; }
        n -= i >>> 31;
        return n;
}

这个地方采用的是分治法. (可以想想二分搜索的过程)
意思就是通过划分16，8，4，2等逐步缩小的四个区间进行判断和移位。不管if的代码块是否执行，需要判断的位的区间也在随着代码的推进而逐步缩减。它通过分层次的缩小需要求解的域的范围，减少计算次数. 

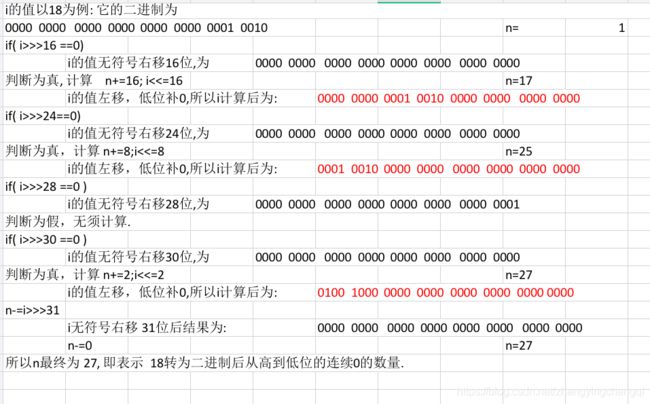
分析过程如下: 

if( i>>>30==0 )判断完后还有两位，为什么最后 n-= i>>>31,  这里i 右移了31位，等于只留下了最高位，那么第二高位怎么没有处理呢?

   因为，在方法的开始已经判断并返回了变量为0即所有的位均为0的情况，所以能进行到后面的代码部分，说明变量不为0，即必然存在至少一个位为1，而我们在选择需要讨论的位区间时，始终选择的是包含位为1的区间进行讨论。所以，在最后区间长度变为2时，区间中必然至少存在一位是1，而我们讨论的是高位连续的0的个数，如果区间第一位为1，那么第二位自然不用讨论。如果区间第一位是0，那么第二位必然是1，也不需要讨论。所以这里只用讨论第一位的情况

3. formatUnsignedInt()

    经过上面的以数字18为例的计算后，我们可以得到18的二进制高位会出现连续的 27个0, 接下来我们回到toUnsignedString()函数看程序. 

//以18为例
private static String toUnsignedString0(int val, int shift) {

        int mag = Integer.SIZE - Integer.numberOfLeadingZeros(val);  // mag=5
        int chars = Math.max(((mag + (shift - 1)) / shift), 1);    //  chars=5
        char[] buf = new char[chars];    

        formatUnsignedInt(val, shift, buf, 0, chars);

        // Use special constructor which takes over "buf".
        return new String(buf, true);
}

它声明了buf字符数组，长度为  5. 接着调用  formatUnsignedInt(   18, 1, buf, 0, 5);  下面分析这个函数的源码: 

// val=18  shift=1     offset=0   len=5
static int formatUnsignedInt(int val, int shift, char[] buf, int offset, int len) {
        int charPos = len;      // 5
        int radix = 1 << shift;   // 左移位，将运算数的二进制整体左移指定位数，低位用0补齐
        //这样二进制的radix为  10(对应10进制为2)  八进制为 1000 (对应10进制为8)  十六进制为 1 0000(对应10进制为16)
        int mask = radix - 1; 
                 // mask为掩码 
                 // 如要转为二进制时mask为1  转为八进制为7   转为十六进制为15
                 // 用二进制表示分别为  1          111          1111
        do {
            buf[offset + --charPos] = Integer.digits[val & mask];
                    // val & mask 相当于一个%(mask+1)运算,它计算出 val对应 mask 这个进制的余数，这个数正好可以对应到 digits中的下标，。 接着通过 Integer.digits取出它的值. 存到 buf数组对应位置
            val >>>= shift;    //再将  val 右移shift位，相当于 /(shift+1). 
            
            //以上对应的就是十进制转n进制的 模n取余法的算法实现了. 
        } while (val != 0 && charPos > 0);

        return charPos;
}

以上调用了   Integer.digits 静态数组. 如下: 

 final static char[] digits = {
        '0' , '1' , '2' , '3' , '4' , '5' ,
        '6' , '7' , '8' , '9' , 'a' , 'b' ,
        'c' , 'd' , 'e' , 'f' , 'g' , 'h' ,
        'i' , 'j' , 'k' , 'l' , 'm' , 'n' ,
        'o' , 'p' , 'q' , 'r' , 's' , 't' ,
        'u' , 'v' , 'w' , 'x' , 'y' , 'z'
};

八进制和十六进制的原理一样，大家可以自行分析.