三维空间刚体运动4-3:四元数线性插值方法:Squad
三维空间刚体运动4-3:四元数线性插值方法:Squad
- 1. Squad的引出
- 2. B e ˊ z i e r c u r v e B\acute{e}zier \space curve Beˊzier curve
-
- 2.1 曲线的引出
- 2.2 公式形式及动画演示
- 3. 样条
-
- 3.1 基本概念
- 3.2 样条曲线
- 4. 贝塞尔样条
-
- 4.1 基本概念
- 4.2 Squad中的三次贝塞尔样条
- 5. de Casteljau算法和Quad算法
-
- 5.1 de Casteljau算法
- 5.2 Quad算法
- 6. Squad算法
-
- 6.1 Squad公式形式
- 6.2 连续一阶可导性证明
-
- 6.2.1 连续性证明
- 6.2.2 一阶可微性( C 1 C_{1} C1)证明
- 6.3 Squad产生的插值曲线
- 6. 代码实现
- 参考文献:
本篇系列文章参照高翔老师《视觉SLAM十四讲从理论到实践》,讲解三维空间刚体运动。博文将原第三讲分为四部分来讲解,其中四元数部分较多较复杂,又分为四部分,总体目录如下:
- 旋转矩阵和变换矩阵;
- 旋转向量表示旋转;
- 欧拉角表示旋转;
- 四元数包括以下部分:
4-1. 四元数表示变换;
4-2. 四元数线性插值方法:LinEuler/LinMat/Lerp/Nlerp/Slerp;
4-3. 四元数多点插值方法:Squad;
4-4. 四元数多点二次插值方法:Spring。
本文相对于原文会适当精简,同时为便于全面理解,会收集其他网络好文,根据作者理解,加入一些注解和扩展知识点,如果您觉得还不错,请一键四连(点赞关注收藏评论),让更多的人看到。
1. Squad的引出
当在两个旋转之间做插值时,Slerp是最优的。但是对于单位四元数集合,Slerp插值曲线差不多等同于一条直线(但在表面是圆弧)。此时多点旋转之间的插值会出现以下问题:
- 插值曲线在控制点(即 p 1 , p 2 . . . p_{1},p_{2}... p1,p2...)不是平滑的;
- 角速度不是常量;
- 角速度在控制点处不连续。
如下图所示:

虽然再参数化(Reparameterization)可以确保整个插值曲线的连续性,实际上插值参数会被转换成关键帧之间一系列离散的帧,因此一个再参数化的插值曲线与分配到的每个关键帧之间的间隙大小有关。两个关键帧插值 q i , q i + 1 q_{i},q_{i+1} qi,qi+1的间隙与它们之间的夹角 θ \theta θ大小成正比,夹角 θ \theta θ可由 cos θ = q i ⋅ q i + 1 \cos\theta=q_{i}\cdot q_{i+1} cosθ=qi⋅qi+1给出。
由于每个子间隙之间的帧数必须是整数,因此角速度只能接近常量,而达不到常量,对比图1.1和图1.2。

然而想要插值曲线变得平滑并不容易,比如类似下面这种情况:平面上两点间插值一条直线很简单,但是即使在最简单的欧式空间中,在多点间创建一条平滑插值曲线也是相当困难的,如图1.3中所示: a ) a) a)表示平面两点间的直线简单插值曲线; b ) b) b)表示多点间的线性插值曲线,关键点处不可微; c ) c) c)表示为保证可微性而使用的三次曲线,比如样条。

我们希望能以牺牲固定角速度为条件,让插值的曲线不仅是平滑连续的,而且让它的一阶甚至是高阶导数是连续的(曲线连续我们称为 C 0 C^{0} C0连续,达到一阶导数连续就叫做 C 1 C^{1} C1连续,在此基础上达到二阶导数连续叫做 C 2 C^{2} C2连续,以此类推)。注意:这里之所以牺牲角速度,是因为在实际应用中更注重路线,而不是特定的角速度。
解决这个问题的方法有很多,在网上能找到很多论文,但是每一种方法想要完全理解都不是那么容易的,而且它们一般都比普通的Slerp或者Nlerp要慢得多。我们在这里只会简单介绍最常见到而且也是最直观的球面四边形插值 (Spherical and quadrangle),或称Squad。
Squad仍然是平面上的向量插值衍生到超球面的结果,所以我们关注的重点首先仍然是向量的插值。平面上多点间插值有多种使用三次曲线的插值方法,比如 B e ˊ z i e r B\acute{e}zier Beˊzier曲线。Squad也用到了 B e ˊ z i e r B\acute{e}zier Beˊzier曲线,因此在具体介绍Squad之前,先详细了解下 B e ˊ z i e r c u r v e B\acute{e}zier \space curve Beˊzier curve和样条的知识。
2. B e ˊ z i e r c u r v e B\acute{e}zier \space curve Beˊzier curve
下面的内容可能会需要一些 B e ˊ z i e r B\acute{e}zier Beˊzier曲线以及样条的前置知识,但即便你不知道也没有关系,我会在下面大致的讲解这些知识。
2.1 曲线的引出
假设我们有一个向量的序列 v 0 , v 1 , . . . , v n \mathbf{v_{0}},\mathbf{v_{1}},...,\mathbf{v_{n}} v0,v1,...,vn,如果我们想对这个序列进行插值,那么我们可以分别对每一对向量 v i \mathbf{v_{i}} vi和 v i + 1 \mathbf{v_{i+1}} vi+1进行插值,然后将插值的曲线连接起来,也就是我们所说的样条(Spline)。如果直接使用Lerp的话,我们会得到这样的结果(假设我们只有五个向量需要插值 v 0 , v 1 , v 2 , v 3 , v 4 \mathbf{v_{0}},\mathbf{v_{1}},\mathbf{v_{2}},\mathbf{v_{3}},\mathbf{v_{4}} v0,v1,v2,v3,v4):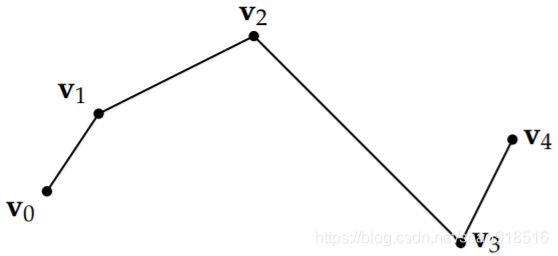
很明显,这个曲线虽然是连续的,但是它的一阶导数(切线)在切换插值向量时都不是连续的。为了解决这个问题,我们最常使用的就是贝塞尔曲线。
贝塞尔曲线( B e ˊ z i e r c u r v e B\acute{e}zier\space curve Beˊzier curve),又称贝兹曲线或贝济埃曲线,是在1962年由法国数学家皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名,称为贝塞尔曲线。贝塞尔曲线为计算机矢量图形学奠定了基础,它的主要意义在于无论是直线或曲线都能在数学上予以描述。它是应用于二维图形应用程序的数学曲线,一般的矢量图形软件通过它来精确画出曲线。我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。
贝塞尔曲线是计算机图形图像造型的基本工具,是图形造型运用得最多的基本线条之一,它由起始点、终止点(也称锚点或数据点,anchor point or data point)、控制点或辅助点(control point or auxiliary point)组成,通过调整控制点(通常有两个或两个以上)调整位于曲线中央的控制线(这条线是虚拟的,中间与贝塞尔曲线交叉,两端是控制端点)。移动两端的端点时贝塞尔曲线改变曲线的曲率(弯曲的程度);移动控制点(也就是移动虚拟的控制线)在起始点和终止点锁定的情况下做均匀移动,绘制出的一条光滑曲线。贝塞尔曲线变化时像可伸缩的皮筋,而贝塞尔曲线的有趣之处更在于它的“皮筋效应”,也就是说,随着点有规律地移动,曲线将产生皮筋伸引一样的变换,带来视觉上的冲击。注意,贝塞尔曲线上的所有控制点、节点均可编辑。这种“智能化”的矢量线条为艺术家提供了一种理想的图形编辑与创造的工具。
2.2 公式形式及动画演示
贝塞尔曲线公式有多种形式,根据未知数 t t t的最高次幂划分,包括线性公式、二次方公式、三次方公式及N次方的通用形式。也可以根据控制点的个数分为一阶贝塞尔曲线(0个控制点)、二阶贝塞尔曲线(1个控制点)、三阶贝塞尔曲线(2个控制点)等等。贝塞尔曲线具有以下特征:
- 曲线通过起点和终点,并与特征多边形首末两边相切于起点和终点,中间点将曲线拉向自己;
- 平面离散点控制曲线的形状,改变一个离散点的坐标,曲线的形状将随之改变(点对曲线具有整体控制性);
- 曲线落在特征多边形的凸包之内,它比特征多边形更趋于光滑。
下面我们看一下它们的公式形式及动画演示:
-
线性公式(一阶贝塞尔曲线)
给定点 P 0 , P 1 P_{0},P_{1} P0,P1,线性贝兹曲线只是一条两点之间由连续点组成的线段。这条线段由下式给出: B ( t ) = P 0 + ( P 1 − P 0 ) t = P 0 ( 1 − t ) + P 1 t , t ∈ [ 0 , 1 ] (2.1) B(t)=P_{0}+(P_{1}-P_{0})t=P_{0}(1-t)+P_{1}t,t\in[0,1]\tag{2.1} B(t)=P0+(P1−P0)t=P0(1−t)+P1t,t∈[0,1](2.1)
其等同于线性插值,插值过程演示如下:
-
二次方公式(二阶贝塞尔曲线)
二次方贝兹曲线的路径由给定点 P 0 , P 1 , P 2 P_{0},P_{1},P_{2} P0,P1,P2的函数 B ( t ) B(t) B(t)追踪: B ( t ) = P 0 ( 1 − t ) 2 + P 1 2 t ( 1 − t ) + P 2 t 2 , t ∈ [ 0 , 1 ] (2.2) B(t)=P_{0}(1-t)^{2}+P_{1}2t(1-t)+P_{2}t^{2},t\in[0,1]\tag{2.2} B(t)=P0(1−t)2+P12t(1−t)+P2t2,t∈[0,1](2.2)
描述一条抛物线,其动画演示如下:
-
三次方公式(三阶贝塞尔曲线)
P 0 , P 1 , P 2 , P 2 P_{0},P_{1},P_{2},P_{2} P0,P1,P2,P2四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于 P 0 P_{0} P0走向 P 1 P_{1} P1,并从 P 2 P_{2} P2的方向来到 P 3 P_{3} P3,一般不会经过 P 1 P_{1} P1或 P 2 P_{2} P2,这两个点只是在那里提供方向资讯。 P 0 P_{0} P0和 P 1 P_{1} P1之间的间距,决定了曲线在转而趋进 P 3 P_{3} P3之前,走向 P 2 P_{2} P2方向的“长度有多长”。
曲线的参数形式为: B ( t ) = P 0 ( 1 − t ) 3 + 3 P 1 t ( 1 − t ) 2 + 3 P 2 t 2 ( 1 − t ) + P 3 t 3 , t ∈ [ 0 , 1 ] (2.3) B(t)=P_{0}(1-t)^{3}+3P_{1}t(1-t)^{2}+3P_{2}t^{2}(1-t)+P_{3}t^{3},t\in[0,1]\tag{2.3} B(t)=P0(1−t)3+3P1t(1−t)2+3P2t2(1−t)+P3t3,t∈[0,1](2.3)
现代的成象系统,如PostScript、Asymptote和Metafont,运用了以贝兹样条组成的三次贝兹曲线,用来描绘曲线轮廓。动画演示如下:

-
一般参数公式
n n n阶贝兹曲线可如下推断。给定点P0、P1、…、Pn,其贝兹曲线即: B ( t ) = ∑ i = 0 n ( n i ) P i ( 1 − t ) n − i t i = ( n 0 ) P 0 ( 1 − t ) n t 0 + ( n 1 ) P 1 ( 1 − t ) n − 1 t 1 + . . . + ( n n ) P n ( 1 − t ) 0 t n , t ∈ [ 0 , 1 ] (2.4) B(t)=\sum_{i=0}^{n}\binom{n}{i}P_{i}(1-t)^{n-i}t^{i}=\binom{n}{0}P_{0}(1-t)^{n}t^{0}+\binom{n}{1}P_{1}(1-t)^{n-1}t^{1}+...+\binom{n}{n}P_{n}(1-t)^{0}t^{n},t\in[0,1]\tag{2.4} B(t)=i=0∑n(in)Pi(1−t)n−iti=(0n)P0(1−t)nt0+(1n)P1(1−t)n−1t1+...+(nn)Pn(1−t)0tn,t∈[0,1](2.4)
在这里展示一下四次及五次贝塞尔曲线的动画形式,其方程可参照一般参数公式。四次贝塞尔曲线的动画形式:
五次贝塞尔曲线的动画形式:
一般参数公式包括递归表达及其展开式,公式说明如下:
1.开始于P0并结束于Pn的曲线,即所谓的端点插值法属性;
2.曲线是直线的充分必要条件是所有的控制点都位于曲线上。同样的,贝塞尔曲线是直线的充分必要条件是控制点共线;
3.曲线的起始点(结束点)相切于贝塞尔多边形的第一节(最后一节)。
4.一条曲线可在任意点切割成两条或任意多条子曲线,每一条子曲线仍是贝塞尔曲线;
5.一些看似简单的曲线(如圆)无法以贝塞尔曲线精确的描述,或分段成贝塞尔曲线(但可以小于千分之一的最大半径误差近似于圆);
6.位于固定偏移量的曲线(来自给定的贝塞尔曲线),又称作偏移曲线(假平行于原来的曲线,如两条铁轨之间的偏移)无法以贝兹曲线精确的形成(某些琐屑实例除外)。无论如何,现存的启发法通常可为实际用途中给出近似值。
到此,我们就有了足够的贝塞尔曲线知识。只要有足够的控制点,任何曲线都可以使用贝塞尔方法绘制。这个说法听上去很美好,但是在实际的曲线设计过程中,一条复杂的贝塞尔曲线的生成是计算高成本的(computationally expensive)。试想一下,如果要设计一条经过12个固定点的曲线,最后生成的曲线方程就是12次的(t的指数的最高次数为12),那么每次微调这些控制点位置,计算机需要重新拟合这条复杂方程式,严重影响计算效率。因此,人们就想出样条线(Spline)方法来完成点的多项式拟合。
3. 样条
3.1 基本概念
样条意思是指通过一组给定点集来生成平滑曲线的柔性带。此概念源于生产实践,“样条”是绘制曲线的一种绘图工具,是富有弹性的细长条。绘图时用压铁使样条通过指定的形值点(样点),并调整样条使它具有满意的形状,然后沿样条画出曲线。
在数学学科数值分析中,样条是一种特殊的函数,由多项式分段定义。样条的英语单词spline来源于可变形的样条工具,那是一种在造船和工程制图时用来画出光滑形状的工具。在中国大陆,早期曾经被称做“齿函数”。后来因为工程学术语中“放样”一词而得名。
在计算机科学的计算机辅助设计和计算机图形学中,样条通常是指分段定义的多项式参数曲线。虽然样条线可以采用单段和多段的方式创建,但对于单段样条线来说。阶次=点数-1,因此单段样条线最多只能使用25个点。单段构造方式受到一定的限制,定义点的数量越多,样条线的阶次越高,而阶次越高样条线会出现意外结果,如变形等。而且单段样条线不能封闭,因此不建议使用单段构造样条线。另外,多段样条线的阶次由用户自己定义(≤24),样条线定义点数量没有限制。但至少比阶次多一点。在设计中,通常采用3~5阶样条线。由于多段样条构造简单,使用方便,拟合准确,并能近似曲线拟合和交互式曲线设计中复杂的形状,所以多段样条是这些领域中曲线的常用表示方法。
在插值问题中,样条插值通常比多项式插值好用。用低阶的样条插值能产生和高阶的多项式插值类似的效果,并且可以避免被称为龙格现象的数值不稳定的出现。并且低阶的样条插值还具有“保凸”的重要性质。
3.2 样条曲线
样条曲线(Spline Curves): 是给定一系列控制点而得到的一条曲线,曲线形状由这些点控制。一般分为插值样条和拟合样条,插值是在原有数据点上进行填充生成曲线,曲线必经过原有数据点;拟合是依据原有数据点,通过参数调整设置,使得生成曲线与原有点差距最小(最小二乘),因此曲线未必会经过原有数据点。
所谓的样条曲线就是分段多项式(Piecewise Polynomials),所谓的“分段”,就是在不同的定义域区间里面,y值对应的表达式是不一样的。样条曲线起源于一个常见问题,即已知若干点的条件下,如何得到通过这些点的一条光滑曲线?
一个简单且行之有效的方法是,把这些点作为限制点(即锚点),然后在这些限制点中放置一条具有弹性的金属片,最后金属片绕过这些点后的最终状态即为所需曲线。而最终得到的形状曲线,就是样条曲线。这也是该名字的由来,其中金属片就是样条,形成的曲线就是样条曲线。如下图:

样条曲线是构建自由曲面的重要曲线,可以是平面样条,也可以是空间样条;可以封闭,也可以开环,可以是单段样条线,也可以是多段样条线。
4. 贝塞尔样条
4.1 基本概念
从编辑便捷性角度看,分段多项式较单一段贝塞尔曲线有优势,因为若需要调整曲线局部,只需要调整分段多项式里面的一条式子即可,其他式子维持不变,这样计算机不需要耗费额外资源,重新计算整条12次方的曲线方程。但现在问题又来了,样条线的每个分段,是怎样的多项式呢?比如下图这12个点,我们最容易想象到的,就是点与点之间,按顺序两两相连,每个分段多项式,都是最简单线性方程。

但是这样显然是不够的,因为这样转角尖锐的效果,不能模拟高次多项式的平滑效果。于是,计算机图形学界,达到了一个共识:样条线的每个分段多项式,使用n = 3的贝塞尔曲线(参考上面动图)。之所以采用三次曲线,是因为三次样条函数要求在各个节点(插值点)处函数值、一阶导数值、二阶导数值连续。这个要求同时具有明显的几何与力学意义。从几何角度而言,最高到二阶导数连续的函数在各节点上光滑且对称地连续,即在节点处左右微小范围内该样条函数是一段圆弧,曲率半径相等。因为细梁(样条函数)的弯矩与曲率成正比,因此在力学意义上,三次样条函数等价于将弹性杆压在各节点处自然弯曲所得到的结果。使用贝塞尔曲线连接的各点如下图:

使用n = 3的贝塞尔曲线原因是要限定相邻的两个分段多项式,在交接点位置的一阶导数相等(斜率相等)和二阶导数相等(斜率的变化率相等),这里留作第五节的证明。直观来看,就是让所有分段曲线能够平滑顺畅地连接起来,最终与单条的高次贝塞尔曲线在形状上没有区别。这里的每一个分段,就称为贝塞尔样条线(Bezier Spline)。各位熟悉的矢量编辑软件,如Illustrator,Coreldraw,inkscape,Gimp等,都是使用这个原理生成曲线,并可以通过每个控制点的把柄(Handles,实质也是控制点)来调整弯曲程度。
除了贝塞尔样条,另外一种贝塞尔曲线的变种是B样条。针对贝塞尔曲线在外形设计的应用中存在一些具体的不足之处,主要有一下三点:
- 确定了多边形的顶点数(m个),也就决定了所定义的Bezier曲线的阶次(m-1次),这样很不灵活;
- 当顶点数(m)较大时,曲线的阶次将比较高。此时,多边形对曲线形状的控制将明显减弱;
- Bezier的调和函数的值,在开区间(0,1)内均不为0。因此,所定义的曲线在(0
为了克服以上提到的在Bezier曲线中存在的问题,Gordon、Riesenfeld和Forrest等人拓展了Bezier曲线,用n次B样条基函数替换了伯恩斯坦基函数,构造了B样条曲线。B样条曲线除了保持Bezier曲线所具有的有点外,还增加了可以对曲线进行局部修改这一突出的优点。除此之外,它还具有对特征多边形更逼近以及多项式阶次较低等优点。因此,B样条曲线在外形设计中得到了更广泛的重视和应用。
B样条曲线曲面源于20世纪70年代早期Pierre Bézier的开创性工作。某种意义上,人们可以认为B样条曲线曲面是贝塞尔曲线曲面之“子”,而非均匀有理B样条(non-uniform rational b-spline, NURBS)是Bézier曲线曲面之“孙”.从时间上大致是对的,他们无疑已经走向成熟。对于B样条曲线和NURBS,本篇没有用到,故这里不再详细讲解。感兴趣的同学,B样条曲线可以参考参考文献7,NURBS可以参考参考文献8。
总结:贝塞尔曲线是由两端的起始点和终止点(也可称为锚点或数据点)构成,并有控制点控制方向的曲线,它并不通过控制点。样条由各个锚点组成,样条曲线穿过每个锚点,两两锚点之间可由任意曲线链接。样条中两两锚点使用贝塞尔曲线连接的话,就称之为贝塞尔样条。
好了,终于铺垫完前置知识,下面看如何根据Squad中贝兹样条及推导算法。
4.2 Squad中的三次贝塞尔样条
回到第二节提到的插值问题,对于 v 0 , v 1 , v 2 , v 3 , v 4 \mathbf{v_{0}},\mathbf{v_{1}},\mathbf{v_{2}},\mathbf{v_{3}},\mathbf{v_{4}} v0,v1,v2,v3,v4进行Lerp插值形成的曲线,如图2.1。很明显,这个曲线虽然是连续的,但是它的一阶导数(切线)在切换插值向量时都不是连续的。我们一开始的想法可能会是将中间的 v 1 , v 2 , v 3 \mathbf{v_{1}},\mathbf{v_{2}},\mathbf{v_{3}} v1,v2,v3作为控制点,直接使用一个四阶 B e ˊ z i e r B\acute{e}zier Beˊzier曲线(因为有五个点)来生成这个近似曲线。但是 B e ˊ z i e r B\acute{e}zier Beˊzier曲线只会经过初始点与最终点(插值),一般不会经过中间的控制点(近似),所以这样求出来的曲线虽然是可导的,但是插值曲线不会经过中间的三个向量:

为了解决这个问题,我们可以分段对每两个向量 v i \mathbf{v_{i}} vi和 v i + 1 \mathbf{v_{i+1}} vi+1之间使用 Bézier曲线进行插值,之后将所有的曲线(即贝塞尔样条)连接起来。因为我们需要让曲线的一阶导数(或者说曲线的趋势)连续,我们还需要知道它们的前一个向量 v i − 1 \mathbf{v_{i-1}} vi−1和后一个向量 v i + 2 \mathbf{v_{i+2}} vi+2,并且用它们生成两个控制点 s i \mathbf{s_{i}} si和 s i + 1 \mathbf{s_{i+1}} si+1来控制曲线的趋势。我们会使用 v i \mathbf{v_{i}} vi和 v i + 1 \mathbf{v_{i+1}} vi+1作为端点(曲线会经过这两个点), s i \mathbf{s_{i}} si和 s i + 1 \mathbf{s_{i+1}} si+1作为中间的控制点,使用一个三次贝塞尔样条(Cubic Bézier Spline,四个点)来近似这个两个向量之间的插值。
在我们的例子中,因为我们一共有四对向量( v 0 v 1 \mathbf{v_{0}}\mathbf{v_{1}} v0v1、 v 1 v 2 \mathbf{v_{1}}\mathbf{v_{2}} v1v2、 v 2 v 3 \mathbf{v_{2}}\mathbf{v_{3}} v2v3、 v 3 v 4 \mathbf{v_{3}}\mathbf{v_{4}} v3v4),我们会使用四个三次贝兹曲线对这五个点进行插值。我们知道,对于三次贝兹曲线所产生的样条,如果想让最终的插值曲线达到 C 1 C_{1} C1连续,则需要让前一个样条在 s i \mathbf{s_{i}} si的控制点与当前样条在 s i \mathbf{s_{i}} si的控制点分别处于最终曲线在 s i \mathbf{s_{i}} si处切线对等的两侧:

在上面的曲线中,蓝色的线就是曲线在点 s i \mathbf{s_{i}} si处的切线,红色的点就是三次Bézier样条的控制点 s i \mathbf{s_{i}} si,分别处于切线对等的两侧( s i \mathbf{s_{i}} si的推导方法放在 5.1 5.1 5.1)。对于两个端点 v 0 \mathbf{v_{0}} v0和 v 4 \mathbf{v_{4}} v4,我们直接将这两个向量的控制点取为它们本身(这不是唯一的做法,但这样是可行的),最终得到一个平滑的曲线。
我们希望将类似的逻辑带到四元数的超球面上,得到四元数序列的插值的方法,但在此之前我们需要了解如何使用de Casteljau算法构造一个三次 Bézier曲线。
5. de Casteljau算法和Quad算法
注意,Quad算法是对de Casteliau算法的简化。
5.1 de Casteljau算法
Bézier曲线的构造有个著名的递归算法叫做de Casteljau算法(de Casteljau’s Algorithm),它对任意次方的 Bézier 曲线都是成立的,但是这里我们只关注三次Bézier曲线的情况。
这个算法最基本的思想就是线性插值的嵌套。假设我们有四个向量
v 0 , v 1 , v 2 , v 3 \mathbf{v_{0}},\mathbf{v_{1}},\mathbf{v_{2}},\mathbf{v_{3}} v0,v1,v2,v3(这里容易混淆,可依次看做 v i , s i , s i + 1 , v i + 1 \mathbf{v_{i}},\mathbf{s_{i}},\mathbf{s_{i+1}},\mathbf{v_{i+1}} vi,si,si+1,vi+1),那么我们可以这样子获得最终的三次 Bézier 曲线:
首先,我们对每一对向量 v 0 v 1 \mathbf{v_{0}}\mathbf{v_{1}} v0v1、 v 1 v 2 \mathbf{v_{1}}\mathbf{v_{2}} v1v2、 v 2 v 3 \mathbf{v_{2}}\mathbf{v_{3}} v2v3进行线性插值,获得 v 01 \mathbf{v_{01}} v01、 v 12 \mathbf{v_{12}} v12、 v 23 \mathbf{v_{23}} v23: v 01 = L e r p ( v 0 , v 1 ; t ) v 12 = L e r p ( v 1 , v 2 ; t ) v 23 = L e r p ( v 2 , v 3 ; t ) \begin{aligned} &\mathbf{v_{01}}=Lerp(\mathbf{v_{0}},\mathbf{v_{1}};t) \\&\mathbf{v_{12}}=Lerp(\mathbf{v_{1}},\mathbf{v_{2}};t) \\&\mathbf{v_{23}}=Lerp(\mathbf{v_{2}},\mathbf{v_{3}};t) \end{aligned} v01=Lerp(v0,v1;t)v12=Lerp(v1,v2;t)v23=Lerp(v2,v3;t)之后,我们对 v 01 v 12 \mathbf{v_{01}}\mathbf{v_{12}} v01v12 和 v 12 v 23 \mathbf{v_{12}}\mathbf{v_{23}} v12v23这两对向量进行线性插值,获得 v 012 \mathbf{v_{012}} v012和 v 123 \mathbf{v_{123}} v123: v 012 = L e r p ( v 01 , v 12 ; t ) v 123 = L e r p ( v 12 , v 23 ; t ) \begin{aligned} &\mathbf{v_{012}}=Lerp(\mathbf{v_{01}},\mathbf{v_{12}};t) \\&\mathbf{v_{123}}=Lerp(\mathbf{v_{12}},\mathbf{v_{23}};t) \end{aligned} v012=Lerp(v01,v12;t)v123=Lerp(v12,v23;t)最后,对 v 012 \mathbf{v_{012}} v012和 v 123 \mathbf{v_{123}} v123进行线性插值获得 v 0123 \mathbf{v_{0123}} v0123,这个向量就是我们想要的最终结果,它就是三次 Bézier 曲线上的点: v 0123 = L e r p ( v 012 , v 123 ; t ) (5.1) \mathbf{v_{0123}}=Lerp(\mathbf{v_{012}},\mathbf{v_{123}};t)\tag{5.1} v0123=Lerp(v012,v123;t)(5.1)虽然这个算法看起来很繁琐,但是我们可以通过一张图来理解它(取 t = 0.4 t=0.4 t=0.4):

可以看到,虽然我们一直在使用线性插值,最终获得的却是一条三次 Bézier曲线(黑色的线)。
如果将这些式子合并起来,我们就能得到三次 Bézier 曲线的递归公式。因为这个式子太长了,我将 L e r p ( v i , v i + 1 ; t ) Lerp(\mathbf{v_{i}},\mathbf{v_{i+1}};t) Lerp(vi,vi+1;t)简写为 L ( v i , v i + 1 ; t ) L(\mathbf{v_{i}},\mathbf{v_{i+1}};t) L(vi,vi+1;t),得到三次 Bézier 曲线的递归公式: B e ˊ z i e r ( v 0 , v 1 , v 2 , v 3 ; t ) = L ( L ( L ( v 0 , v 1 ; t ) , L ( v 0 , v 1 ; t ) ; t ) , L ( L ( v 0 , v 1 ; t ) , L ( v 0 , v 1 ; t ) ; t ) ; t ) (5.2) B\acute{e}zier(\mathbf{v_{0}},\mathbf{v_{1}},\mathbf{v_{2}},\mathbf{v_{3}};t)=L(L(L(\mathbf{v_{0}},\mathbf{v_{1}};t),L(\mathbf{v_{0}},\mathbf{v_{1}};t);t),L(L(\mathbf{v_{0}},\mathbf{v_{1}};t),L(\mathbf{v_{0}},\mathbf{v_{1}};t);t);t)\tag{5.2} Beˊzier(v0,v1,v2,v3;t)=L(L(L(v0,v1;t),L(v0,v1;t);t),L(L(v0,v1;t),L(v0,v1;t);t);t)(5.2)
如果将 L e r p Lerp Lerp的定义 L e r p ( v i , v i + 1 ; t ) = ( 1 − t ) v i + t v i + 1 Lerp(\mathbf{v_{i}},\mathbf{v_{i+1}};t)=(1-t)\mathbf{v_{i}}+t\mathbf{v_{i+1}} Lerp(vi,vi+1;t)=(1−t)vi+tvi+1不断代入并展开的话,我们能获得这样一个式子: B e ˊ z i e r ( v 0 , v 1 , v 2 , v 3 ; t ) = ( 1 − t ) 3 v 0 + 3 ( 1 − t ) 2 t v 1 + 3 ( 1 − t ) t 2 v 2 + t 3 v 3 (5.3) B\acute{e}zier(\mathbf{v_{0}},\mathbf{v_{1}},\mathbf{v_{2}},\mathbf{v_{3}};t)=(1-t)^{3}\mathbf{v_{0}}+3(1-t)^{2}t\mathbf{v_{1}}+3(1-t)t^{2}\mathbf{v_{2}}+t^{3}\mathbf{v_{3}}\tag{5.3} Beˊzier(v0,v1,v2,v3;t)=(1−t)3v0+3(1−t)2tv1+3(1−t)t2v2+t3v3(5.3)因为每项的 t t t的最高次幂都是3,所以我们说它是一个三次Bézier曲线。以上就是de Castelijau算法的全部内容。
我们可以直接将上面的递归公式运用到四元数上,得到四元数的球面Bézier曲线公式,但因为球面的线性插值不是Lerp而是Slerp,我们需要将公式中所有的Lerp全部换成Slerp(你可以想象一下,将四个向量形成的四边形看作是一个网格(Mesh),之后将这个网格贴在球面上)。同样因为公式太长,我会将 S l e r p ( q i , q i + 1 ; t ) Slerp(q_{i},q_{i+1};t) Slerp(qi,qi+1;t)简写为 S ( q i , q i + 1 ; t ) S(q_{i},q_{i+1};t) S(qi,qi+1;t),得到四元数的三次 Bézier 曲线的递归公式:
S B e ˊ z i e r ( q 0 , q 1 , q 2 , q 3 ; t ) = S ( S ( S ( q 0 , q 1 ; t ) , S ( q 1 , q 2 ; t ) ; t ) , S ( S ( q 1 , q 2 ; t ) , S ( q 2 , q 3 ; t ) ; t ) ; t ) (5.4) SB\acute{e}zier(q_{0},q_{1},q_{2},q_{3};t)=S(S(S(q_{0},q_{1};t),S(q_{1},q_{2};t);t),S(S(q_{1},q_{2};t),S(q_{2},q_{3};t);t);t)\tag{5.4} SBeˊzier(q0,q1,q2,q3;t)=S(S(S(q0,q1;t),S(q1,q2;t);t),S(S(q1,q2;t),S(q2,q3;t);t);t)(5.4)
这个其实就是Ken Shoemake在1985年的那篇Paper里提出的插值方法,他也提供了控制点的公式。然而,很明显这个方法实在是太复杂了,仅仅是一个 Slerp 就要使用四个三角函数,而我们这里一共有 7 个 Slerp,如果真的要使用它进行插值会对性能产生非常大的影响。
5.2 Quad算法
于是,Shoemake在1987年提出了一个更高效的近似算法,也就是我们熟悉的Squad。这里容易看晕,我已尽量使推理逻辑严密,请感到晕的读者朋友多看几遍。
我们首先仍然来看平面中向量的情况。我把向量的Squad算法叫做Quad,代表「Quadrangle」,Quad虽有很多歧义,而且我好像没看到别人这么叫过,但是为了简便这里就暂时这样称呼它吧。Quad算法是对de Casteliau算法的简化。
与三次Bézier曲线嵌套了三层一次插值不同,Quad使用的是一层二次插值嵌套了一层一次插值。我们首先是分别对 v 0 v 3 \mathbf{v_{0}}\mathbf{v_{3}} v0v3和 v 1 v 2 \mathbf{v_{1}}\mathbf{v_{2}} v1v2进行插值,获得 v 03 \mathbf{v_{03}} v03和 v 12 \mathbf{v_{12}} v12: v 03 = L e r p ( v 0 , v 3 ; t ) v 12 = L e r p ( v 1 , v 2 ; t ) \begin{aligned} &\mathbf{v_{03}}=Lerp(\mathbf{v_{0}},\mathbf{v_{3}};t) \\&\mathbf{v_{12}}=Lerp(\mathbf{v_{1}},\mathbf{v_{2}};t) \end{aligned} v03=Lerp(v0,v3;t)v12=Lerp(v1,v2;t)之后,我们使用 2 t ( 1 − t ) 2t(1−t) 2t(1−t)为参数,对 v 03 \mathbf{v_{03}} v03和 v 12 \mathbf{v_{12}} v12进行二次插值,获得最终的 v 0312 \mathbf{v_{0312}} v0312: v 0312 = L e r p ( v 03 , v 12 ; 2 t ( 1 − t ) ) (5.5) \mathbf{v_{0312}}=Lerp(\mathbf{v_{03}},\mathbf{v_{12}};2t(1−t)) \tag{5.5} v0312=Lerp(v03,v12;2t(1−t))(5.5)注意最终的Lerp使用的参数是二次的 2 t ( 1 − t ) 2t(1−t) 2t(1−t),不是我们一般使用的 t t t,而且它插值的两个向量也变为了 v 03 \mathbf{v_{03}} v03和 v 12 \mathbf{v_{12}} v12。我们仍然可以使用图片来理解它(取 t = 0.4 t=0.4 t=0.4):

同样,我们可以将 Quad 写为递归形式: Q u a d ( v 0 , v 1 , v 2 , v 3 ; t ) = L e r p ( L e r p ( v 0 , v 3 ; t ) , L e r p ( v 1 , v 2 ; t ) ; 2 t ( 1 − t ) ) (5.6) Quad(\mathbf{v_{0}},\mathbf{v_{1}},\mathbf{v_{2}},\mathbf{v_{3}};t)=Lerp(Lerp(\mathbf{v_{0}},\mathbf{v_{3}};t),Lerp(\mathbf{v_{1}},\mathbf{v_{2}};t);2t(1-t))\tag{5.6} Quad(v0,v1,v2,v3;t)=Lerp(Lerp(v0,v3;t),Lerp(v1,v2;t);2t(1−t))(5.6)
可以看到,这样的插值要比三次Bézier曲线简单很多,将七次Lerp减少到了三次.虽然最终的曲线与三次Bézier曲线不完全相同,但是已经很近似了。我们可以看几个对比,下图中,左边是三次Bézier曲线,右边是Quad曲线:
如果利用Lerp的定义 L e r p Lerp Lerp的定义 L e r p ( v i , v i + 1 ; t ) = ( 1 − t ) v i + t v i + 1 Lerp(\mathbf{v_{i}},\mathbf{v_{i+1}};t)=(1-t)\mathbf{v_{i}}+t\mathbf{v_{i+1}} Lerp(vi,vi+1;t)=(1−t)vi+tvi+1将递归式展开的话,我们能得到这样的式子: Q u a d ( v 0 , v 1 , v 2 , v 3 ; t ) = ( 2 t 2 − 2 t + 1 ) ( 1 − t ) v 0 + 2 ( 1 − t ) 2 t v 1 + 2 ( 1 − t ) t 2 v 2 + ( 2 t 2 − 2 t + 1 ) t v 3 (5.7) Quad(\mathbf{v_{0}},\mathbf{v_{1}},\mathbf{v_{2}},\mathbf{v_{3}};t)=(2t^{2}-2t+1)(1-t)\mathbf{v_{0}}+2(1-t)^{2}t\mathbf{v_{1}}+2(1-t)t^{2}\mathbf{v_{2}}+(2t^{2}-2t+1)t\mathbf{v_{3}}\tag{5.7} Quad(v0,v1,v2,v3;t)=(2t2−2t+1)(1−t)v0+2(1−t)2tv1+2(1−t)t2v2+(2t2−2t+1)tv3(5.7)
它仍是一个三次的曲线,只不过系数有所不同。
6. Squad算法
6.1 Squad公式形式
如果我们将 Quad 的递归公式用于球面,就能得到用于四元数的Squad: S q u a d ( q 0 , q 1 , q 2 , q 3 ; t ) = S l e r p ( S l e r p ( q 0 , q 3 ; t ) , S l e r p ( q 1 , q 2 ; t ) ; 2 t ( 1 − t ) ) (6.1) Squad(q_{0},q_{1},q_{2},q_{3};t)=Slerp(Slerp(q_{0},q_{3};t),Slerp(q_{1},q_{2};t);2t(1-t))\tag{6.1} Squad(q0,q1,q2,q3;t)=Slerp(Slerp(q0,q3;t),Slerp(q1,q2;t);2t(1−t))(6.1)
接下来,我们回到本章最初的主题,对多个单位四元数进行插值.如果我们有一个四元数序列 q 0 , q 1 , . . . , q n q_{0},q_{1},...,q_{n} q0,q1,...,qn,我们希望对每一对四元数 q i q_{i} qi和 q i + 1 q_{i+1} qi+1都使用Squad进行插值,所以我们有: S q u a d ( q i , s i , s i + 1 , q i + 1 ; t ) = S l e r p ( S l e r p ( q i , q i + 1 ; t ) , S l e r p ( s i , s i + 1 ; t ) ; 2 t ( 1 − t ) ) (6.2) Squad(q_{i},s_{i},s_{i+1},q_{i+1};t)=Slerp(Slerp(q_{i},q_{i+1};t),Slerp(s_{i},s_{i+1};t);2t(1-t))\tag{6.2} Squad(qi,si,si+1,qi+1;t)=Slerp(Slerp(qi,qi+1;t),Slerp(si,si+1;t);2t(1−t))(6.2)其中 s i , s i + 1 s_{i},s_{i+1} si,si+1为 q i q_{i} qi和 q i + 1 q_{i+1} qi+1之间的控制点: s i = q i exp ( log ( q i − 1 − 1 q i ) − log ( q i − 1 q i + 1 ) 4 ) (6.3) s_{i}=q_{i}\exp\left (\frac{\log(q^{-1}_{i-1}q_{i})-\log(q^{-1}_{i}q_{i+1})}{4} \right )\tag{6.3} si=qiexp(4log(qi−1−1qi)−log(qi−1qi+1))(6.3)Squad的表达式与Quad类似,不同的是Squad用于球面线性插值而非简单线性插值。Squad的定义形式复杂,因此其产生的插值曲线的连续性和可导性都不明显,下面来证明它的连续性和一阶可导性。
6.2 连续一阶可导性证明
Squad最初由Ken Shoemake于1987年发表,作者在原文中提供了可微性的一般性参考,但是原文已丢失,于是作者又在1997年重新发布了Squad的可微性及控制点 s i s_{i} si的完整证明。
Squad的一阶连续可导性在非控制点处是明显成立的,因为其样条是分段的三次贝塞尔曲线(实际上它是二阶连续可导),现在需要证明其在锚点 q i q_{i} qi也是成立的。
6.2.1 连续性证明
首先,相邻分段在锚点处的值是必须相等的: S q u a d ( q i − 1 , s i − 1 , s i , q i ; 1 ) = S q u a d ( q i , s i , s i + 1 , q i + 1 ; 0 ) 6.4 ) (() Squad(q_{i-1},s_{i-1},s_{i},q_{i};1)=Squad(q_{i},s_{i},s_{i+1},q_{i+1};0)\tag(6.4) Squad(qi−1,si−1,si,qi;1)=Squad(qi,si,si+1,qi+1;0)6.4)(()其中: S q u a d ( q i − 1 , s i − 1 , s i , q i ; 1 ) = S l e r p ( S l e r p ( q i − 1 , q i , 1 ) , S l e r p ( s i − 1 , s i , 1 ) , 0 ) = S l e r p ( q i , s i , 0 ) = q i \begin{aligned}Squad(q_{i-1},s_{i-1},s_{i},q_{i};1) &= Slerp(Slerp(q_{i-1},q_{i},1),Slerp(s_{i-1},s_{i},1),0) \\&= Slerp(qi,si,0) = q_{i}\end{aligned} Squad(qi−1,si−1,si,qi;1)=Slerp(Slerp(qi−1,qi,1),Slerp(si−1,si,1),0)=Slerp(qi,si,0)=qi S q u a d ( q i , s i , s i + 1 , q i + 1 ; 0 ) = S l e r p ( S l e r p ( q i , q i + 1 , 0 ) , S l e r p ( s i , s i + 1 , 0 ) , 0 ) = S l e r p ( q i , s i , 0 ) = q i \begin{aligned}Squad(q_{i},s_{i},s_{i+1},q_{i+1};0) &= Slerp(Slerp(q_{i},q_{i+1},0),Slerp(s_{i},s_{i+1},0),0) \\&= Slerp(qi,si,0) = q_{i}\end{aligned} Squad(qi,si,si+1,qi+1;0)=Slerp(Slerp(qi,qi+1,0),Slerp(si,si+1,0),0)=Slerp(qi,si,0)=qi
因此,Squad在锚点处是连续的。
6.2.2 一阶可微性( C 1 C_{1} C1)证明
下面开始证明Squad在锚点处的连续可微性,即 C 1 C_{1} C1。我们通过推导其在锚点的导数来证明。和上边一样,必须证明下式成立: d d t S q u a d ( q i − 1 , s i − 1 , s i , q i ; 1 ) = d d t S q u a d ( q i , s i , s i + 1 , q i + 1 ; 0 ) 6.5 ) (() \frac{d}{dt}Squad(q_{i-1},s_{i-1},s_{i},q_{i};1)=\frac{d}{dt}Squad(q_{i},s_{i},s_{i+1},q_{i+1};0)\tag(6.5) dtdSquad(qi−1,si−1,si,qi;1)=dtdSquad(qi,si,si+1,qi+1;0)6.5)(()为了证明Squad的导数,这里需要《三维空间刚体运动4-2中》的Slerp的一阶和二阶导数公式(5.15)和(5.16)。另外,我们知道 S l e r p ( q i , q i + 1 ; t ) = q i ( q i ∗ q i + 1 ) t Slerp(q_{i},q_{i+1};t)=q_{i}(q^{*}_{i}q_{i+1})^{t} Slerp(qi,qi+1;t)=qi(qi∗qi+1)t(4-2篇中公式(5-7)),所以我们可以将Squad写成指数形式: S q u a d ( q i , s i , s i + 1 , q i + 1 ; t ) = S l e r p ( q i , q i + 1 ; t ) ( S l e r p ( q i , q i + 1 ; t ) ∗ S l e r p ( s i , s i + 1 ; t ) ) 2 t ( 1 − t ) (6.6) \begin{aligned}Squad(q_{i},s_{i},s_{i+1},q_{i+1};t) &=Slerp(q_{i},q_{i+1};t)\left(Slerp(q_{i},q_{i+1};t)^{*}Slerp(s_{i},s_{i+1};t) \right)^{2t(1-t)}\end{aligned}\tag{6.6} Squad(qi,si,si+1,qi+1;t)=Slerp(qi,qi+1;t)(Slerp(qi,qi+1;t)∗Slerp(si,si+1;t))2t(1−t)(6.6)
引入以下简写: g i ( t ) = S l e r p ( q i , q i + 1 ; t ) ∗ S l e r p ( s i , s i + 1 ; t ) (6.7) g_{i}(t)=Slerp(q_{i},q_{i+1};t)^{*}Slerp(s_{i},s_{i+1};t) \tag{6.7} gi(t)=Slerp(qi,qi+1;t)∗Slerp(si,si+1;t)(6.7)
现在我们开始推导 S q u a d ( q i , s i , s i + 1 , q i + 1 ; t ) Squad(q_{i},s_{i},s_{i+1},q_{i+1};t) Squad(qi,si,si+1,qi+1;t)的导数并决定 s i s^{i} si和 s i + 1 s^{i+1} si+1的取值,以确保样条在锚点处的可微性。类似于Bézier曲线样条,我们同样需要前一个 q i − 1 q_{i-1} qi−1以及 q i + 2 q_{i+2} qi+2的信息。 s i s_{i} si的推导还是比较复杂的,但是它最基本的理念非常简单:让Squad在切换点可导,从而达到 C 1 C_{1} C1连续。也就是说,我们希望 q i − 1 q i q_{i-1}q_{i} qi−1qi插值时在 t = 1 t=1 t=1处的导数,与 q i q i + 1 q_{i}q_{i+1} qiqi+1插值时在 t = 0 t=0 t=0处的导数相等,如公式(6.6)所示。下面我们就来看看 s i s_{i} si的具体推导方法。 S q u a d ( q i , s i , s i + 1 , q i + 1 ; t ) Squad(q_{i},s_{i},s_{i+1},q_{i+1};t) Squad(qi,si,si+1,qi+1;t)的关于 t t t导数为:
d d t S q u a d ( q i , s i , s i + 1 , q i + 1 ; t ) = d d t S l e r p ( S l e r p ( q i , q i + 1 ; t ) , S l e r p ( s i , s i + 1 ; t ) ; 2 t ( 1 − t ) ) = d d t ( S l e r p ( q i , q i + 1 ; t ) g i ( t ) 2 t ( 1 − t ) ) \begin{aligned}\frac{d}{dt}Squad(q_{i},s_{i},s_{i+1},q_{i+1};t) &= \frac{d}{dt}Slerp(Slerp(q_{i},q_{i+1};t),Slerp(s_{i},s_{i+1};t);2t(1-t)) \\&= \frac{d}{dt}\left(Slerp(q_{i},q_{i+1};t)g_{i}(t)^{2t(1-t)}\right)\end{aligned} dtdSquad(qi,si,si+1,qi+1;t)=dtdSlerp(Slerp(qi,qi+1;t),Slerp(si,si+1;t);2t(1−t))=dtd(Slerp(qi,qi+1;t)gi(t)2t(1−t))根据《三维空间刚体运动4-1》中节2.2中的当四元数指数函数微分法则可以得到: d d t S q u a d ( q i , s i , s i + 1 , q i + 1 ; t ) = d d t ( S l e r p ( q i , q i + 1 ; t ) g i ( t ) 2 t ( 1 − t ) ) = ( d d t S l e r p ( q i , q i + 1 ; t ) ) g i ( t ) 2 t ( 1 − t ) + S l e r p ( q i , q i + 1 ; t ) ( d d t g i ( t ) 2 t ( 1 − t ) ) = S l e r p ( q i , q i + 1 ; t ) log ( q i ∗ q i + 1 ) g i ( t ) 2 t ( 1 − t ) + S l e r p ( q i , q i + 1 ; t ) ( d d t g i ( t ) 2 t ( 1 − t ) ) ) (6.8) \begin{aligned}\frac{d}{dt}Squad(q_{i},s_{i},s_{i+1},q_{i+1};t) &= \frac{d}{dt}\left(Slerp(q_{i},q_{i+1};t)g_{i}(t)^{2t(1-t)}\right) \\&= \left(\frac{d}{dt}Slerp(q_{i},q_{i+1};t)\right)g_{i}(t)^{2t(1-t)}+Slerp(q_{i},q_{i+1};t)\left(\frac{d}{dt}g_{i}(t)^{2t(1-t)} \right) \\&= Slerp(q_{i},q_{i+1};t)\log(q^{*}_{i}q_{i+1})g_{i}(t)^{2t(1-t)}+Slerp(q_{i},q_{i+1};t)\left(\frac{d}{dt}g_{i}(t)^{2t(1-t)})\right)\end{aligned}\tag{6.8} dtdSquad(qi,si,si+1,qi+1;t)=dtd(Slerp(qi,qi+1;t)gi(t)2t(1−t))=(dtdSlerp(qi,qi+1;t))gi(t)2t(1−t)+Slerp(qi,qi+1;t)(dtdgi(t)2t(1−t))=Slerp(qi,qi+1;t)log(qi∗qi+1)gi(t)2t(1−t)+Slerp(qi,qi+1;t)(dtdgi(t)2t(1−t)))(6.8)由于 g i ( t ) g_{i}(t) gi(t)是单位四元数的乘积,所以它的值也在单元圆上,因此 g i ( t ) g_{i}(t) gi(t)可以被写为: g i ( t ) = [ cos θ g i ( t ) , sin θ g i ( t ) ) v g i ( t ) ] (6.9) g_{i}(t)=[\cos\theta_{g_{i}(t)},\sin\theta_{g_{i}(t)})\mathbf{v}_{g_{i}(t)}]\tag{6.9} gi(t)=[cosθgi(t),sinθgi(t))vgi(t)](6.9)这里 v g i ( t ) \mathbf{v}_{g_{i}(t)} vgi(t)是单位向量。现在我们可以根据《三维空间刚体运动4-1》中节2.2中的微分法则,来推导 g i ( t ) 2 t ( 1 − t ) g_{i}(t)^{2t(1-t)} gi(t)2t(1−t)的导数: d d t g i ( t ) 2 t ( 1 − t ) = [ − sin ( 2 t ( 1 − t ) θ g i ( t ) ) ( d d t ( 2 t ( 1 − t ) ) θ g i ( t ) + 2 t ( 1 − t ) d d t θ g i ( t ) ) , cos ( 2 t ( 1 − t ) θ g i ( t ) ) ( d d t ( 2 t ( 1 − t ) ) θ g i ( t ) + 2 t ( 1 − t ) d d t θ g i ( t ) ) v g i ( t ) + sin ( 2 t ( 1 − t ) θ g i ( t ) ) d d t v g i ( t ) ] = [ − sin ( 2 t ( 1 − t ) θ g i ( t ) ) ( ( 2 − 4 t ) θ g i ( t ) + 2 t ( 1 − t ) θ g i ′ ( t ) ) , cos ( 2 t ( 1 − t ) θ g i ( t ) ) ( ( 2 − 4 t ) θ g i ( t ) + 2 t ( 1 − t ) θ g i ′ ( t ) ) v g i ( t ) + sin ( 2 t ( 1 − t ) θ g i ( t ) ) v g i ′ ( t ) ] (6.10) \begin{aligned} \frac{d}{dt}g_{i}(t)^{2t(1-t)} &= [-\sin\left(2t(1-t)\theta_{g_{i}(t)}\right )\left( \frac{d}{dt}(2t(1-t))\theta_{g_{i}(t)}+2t(1-t)\frac{d}{dt}\theta_{g_{i}(t)}\right), \\& \quad \cos\left(2t(1-t)\theta_{g_{i}(t)}\right)\left( \frac{d}{dt}(2t(1-t))\theta_{g_{i}(t)}+2t(1-t)\frac{d}{dt}\theta_{g_{i}(t)}\right )\mathbf{v}_{g_{i}(t)}+\sin\left(2t(1-t)\theta_{g_{i}(t)}\right)\frac{d}{dt}\mathbf{v}_{g_{i}(t)}] \\&= [-\sin\left(2t(1-t)\theta_{g_{i}(t)}\right )\left( (2-4t)\theta_{g_{i}(t)}+2t(1-t)\theta_{g_{i}^{'}(t)}\right), \\& \quad \cos\left(2t(1-t)\theta_{g_{i}(t)}\right)\left((2-4t)\theta_{g_{i}(t)}+2t(1-t)\theta_{g_{i}^{'}(t)}\right )\mathbf{v}_{g_{i}(t)}+\sin\left(2t(1-t)\theta_{g_{i}(t)}\right)\mathbf{v}_{g_{i}^{'}(t)}] \end{aligned}\tag{6.10} dtdgi(t)2t(1−t)=[−sin(2t(1−t)θgi(t))(dtd(2t(1−t))θgi(t)+2t(1−t)dtdθgi(t)),cos(2t(1−t)θgi(t))(dtd(2t(1−t))θgi(t)+2t(1−t)dtdθgi(t))vgi(t)+sin(2t(1−t)θgi(t))dtdvgi(t)]=[−sin(2t(1−t)θgi(t))((2−4t)θgi(t)+2t(1−t)θgi′(t)),cos(2t(1−t)θgi(t))((2−4t)θgi(t)+2t(1−t)θgi′(t))vgi(t)+sin(2t(1−t)θgi(t))vgi′(t)](6.10)上面展开了Squad的导数中所有的子表达式,现在我们根据公式(6.5)求出 s i s_{i} si的取值,以使Squad的导数在每个锚点处是连续的。
对于公式(6.5)展开式中的 d d t ( g i − 1 ( t ) 2 t ( 1 − t ) ) \frac{d}{dt}\left( g_{i-1}(t)^{2t(1-t)} \right) dtd(gi−1(t)2t(1−t))和 d d t ( g i ( t ) 2 t ( 1 − t ) ) \frac{d}{dt}\left( g_{i}(t)^{2t(1-t)} \right) dtd(gi(t)2t(1−t)),当 t = 1 t=1 t=1时,将公式(6.10)代入公式(6.8),并使用代数相关计算规则和排版得到: d d t S q u a d ( q i − 1 , s i − 1 , s i , q i ; 1 ) = S l e r p ( q i − 1 , q i ; 1 ) log ( q i − 1 ∗ q i ) + S l e r p ( q i − 1 , q i ; 1 ) ( d d t g i − 1 ( t ) 2 t ( 1 − t ) ) ∣ t = 1 = q i log ( q i − 1 ∗ q i ) + q i [ 0 , − 2 θ g i − 1 ( 1 ) v g i − 1 ( 1 ) ] = q i ( log ( q i − 1 ∗ q i ) − 2 log ( [ cos ( θ g i − 1 ( 1 ) ) , sin ( θ g i − 1 ( 1 ) ) v g i − 1 ( 1 ) ] ) ) = q i ( log ( q i − 1 ∗ q i ) − 2 log ( g i − 1 ( 1 ) ) ) = q i ( log ( q i − 1 ∗ q i ) − 2 log ( q i ∗ s i ) ) \begin{aligned} \frac{d}{dt}Squad(q_{i-1},s_{i-1},s_{i},q_{i};1) &= Slerp(q_{i-1},q_{i};1)\log(q^{*}_{i-1}q_{i})+ Slerp(q_{i-1},q_{i};1)\left( \frac{d}{dt}g_{i-1}(t)^{2t(1-t)} \right )|_{t=1} \\&= q_{i}\log(q^{*}_{i-1}q_{i})+q_{i}[0,-2\theta_{g_{i-1}(1)}\mathbf{v}_{g_{i-1}(1)}] \\&= q_{i}(\log(q^{*}_{i-1}q_{i})-2\log([\cos(\theta_{g_{i-1}(1)}),\sin(\theta_{g_{i-1}(1)})\mathbf{v}_{g_{i-1}(1)}])) \\&= q_{i}(\log(q^{*}_{i-1}q_{i})-2\log(g_{i-1}(1))) \\&= q_{i}(\log(q^{*}_{i-1}q_{i})-2\log(q^{*}_{i}s_{i}))\end{aligned} dtdSquad(qi−1,si−1,si,qi;1)=Slerp(qi−1,qi;1)log(qi−1∗qi)+Slerp(qi−1,qi;1)(dtdgi−1(t)2t(1−t))∣t=1=qilog(qi−1∗qi)+qi[0,−2θgi−1(1)vgi−1(1)]=qi(log(qi−1∗qi)−2log([cos(θgi−1(1)),sin(θgi−1(1))vgi−1(1)]))=qi(log(qi−1∗qi)−2log(gi−1(1)))=qi(log(qi−1∗qi)−2log(qi∗si)) d d t S q u a d ( q i , s i , s i + 1 , q i + 1 ; 0 ) = S l e r p ( q i , q i + 1 ; 0 ) log ( q i ∗ q i + 1 ) + S l e r p ( q i , q i + 1 ; 0 ) ( d d t g i ( t ) 2 t ( 1 − t ) ) ∣ t = 0 = q i log ( q i ∗ q i + 1 ) + q i [ 0 , 2 θ g i ( 0 ) v g i ( 0 ) ] = q i ( log ( q i ∗ q i + 1 ) + 2 log ( [ cos ( θ g i − 1 ( 0 ) ) , sin ( θ g i − 1 ( 0 ) ) v g i − 1 ( 0 ) ] ) ) = q i ( log ( q i ∗ q i + 1 ) + 2 log ( g i ( 0 ) ) ) = q i ( log ( q i ∗ q i + 1 ) + 2 log ( q i ∗ s i ) ) \begin{aligned} \frac{d}{dt}Squad(q_{i},s_{i},s_{i+1},q_{i+1};0) &= Slerp(q_{i},q_{i+1};0)\log(q^{*}_{i}q_{i+1})+ Slerp(q_{i},q_{i+1};0)\left( \frac{d}{dt}g_{i}(t)^{2t(1-t)} \right )|_{t=0} \\&= q_{i}\log(q^{*}_{i}q_{i+1})+q_{i}[0,2\theta_{g_{i}(0)}\mathbf{v}_{g_{i}(0)}] \\&= q_{i}(\log(q^{*}_{i}q_{i+1})+2\log([\cos(\theta_{g_{i-1}(0)}),\sin(\theta_{g_{i-1}(0)})\mathbf{v}_{g_{i-1}(0)}])) \\&= q_{i}(\log(q^{*}_{i}q_{i+1})+2\log(g_{i}(0))) \\&= q_{i}(\log(q^{*}_{i}q_{i+1})+2\log(q^{*}_{i}s_{i}))\end{aligned} dtdSquad(qi,si,si+1,qi+1;0)=Slerp(qi,qi+1;0)log(qi∗qi+1)+Slerp(qi,qi+1;0)(dtdgi(t)2t(1−t))∣t=0=qilog(qi∗qi+1)+qi[0,2θgi(0)vgi(0)]=qi(log(qi∗qi+1)+2log([cos(θgi−1(0)),sin(θgi−1(0))vgi−1(0)]))=qi(log(qi∗qi+1)+2log(gi(0)))=qi(log(qi∗qi+1)+2log(qi∗si))因此 s i s_{i} si必然满足下式: q i ( log ( q i ∗ q i + 1 ) + 2 log ( q i ∗ s i ) ) = q i ( log ( q i − 1 ∗ q i ) − 2 log ( q i ∗ s i ) ) q_{i}(\log(q^{*}_{i}q_{i+1})+2\log(q^{*}_{i}s_{i})) = q_{i}(\log(q^{*}_{i-1}q_{i})-2\log(q^{*}_{i}s_{i})) qi(log(qi∗qi+1)+2log(qi∗si))=qi(log(qi−1∗qi)−2log(qi∗si))由于 q i ∈ H 1 q_{i}\in H_{1} qi∈H1,使用 q i ∗ = q i − 1 q^{*}_{i}=q^{-1}_{i} qi∗=qi−1得到: 4 log ( q i ∗ s i ) = log ( q i − 1 ∗ q i ) − log ( q i ∗ q i + 1 ) q i ∗ s i = exp ( log ( q i − 1 ∗ q i ) − log ( q i ∗ q i + 1 ) 4 ) s i = q i exp ( log ( q i − 1 ∗ q i ) − log ( q i ∗ q i + 1 ) 4 ) = q i exp ( log ( q i − 1 − 1 q i ) − log ( q i − 1 q i + 1 ) 4 ) \begin{aligned} 4\log(q^{*}_{i}s_{i}) &= \log(q^{*}_{i-1}q_{i})-\log(q^{*}_{i}q_{i+1}) \\ q^{*}_{i}s_{i} &= \exp\left(\frac{\log(q^{*}_{i-1}q_{i})-\log(q^{*}_{i}q_{i+1})}{4} \right ) \\ s_{i} &= q_{i}\exp\left(\frac{\log(q^{*}_{i-1}q_{i})-\log(q^{*}_{i}q_{i+1})}{4} \right ) \\ &= q_{i}\exp\left(\frac{\log(q^{-1}_{i-1}q_{i})-\log(q^{-1}_{i}q_{i+1})}{4} \right )\end{aligned} 4log(qi∗si)qi∗sisi=log(qi−1∗qi)−log(qi∗qi+1)=exp(4log(qi−1∗qi)−log(qi∗qi+1))=qiexp(4log(qi−1∗qi)−log(qi∗qi+1))=qiexp(4log(qi−1−1qi)−log(qi−1qi+1)) s i s_{i} si的推导结果和公式(6.3)相同,因此Squad在锚点处使用上式定义的控制点时是连续可微的。
总之,通过以上证明得出结论:Squad在所有分段都是连续且一阶连续可微的。
另外需要注意:
- 和Bézier曲线的样条不同的是,这里的 s i s_{i} si在对 q i q i + 1 q_{i}q_{i+1} qiqi+1插值时和对 q i q i + 1 q_{i}q_{i+1} qiqi+1插值时都是相同的,不像之前是处于切线的两端不同的两个向量。
- 与两个四元数之间的插值一样,Squad同样会受到双重覆盖的影响。我们在计算中间控制点和插值之前,需要先选中一个四元数,比如说 q i q_{i} qi,检测它与其它三个四元数之间的夹角,如果是钝角就翻转,将插值的路线减到最小。
6.3 Squad产生的插值曲线
根据Squad表达式,由四元数 q 0 . . . q n q_{0}...q_{n} q0...qn生成一条插值曲线。但是由于起始控制点 s 0 s_{0} s0和终止控制点 s n s_{n} sn的表达式中分别出现了 q − 1 q_{-1} q−1和 q n + 1 q_{n+1} qn+1l两个未定义的点,因此需要重新定义 s 0 s_{0} s0和 s n s_{n} sn为恰当值(sound value)。最简单的解决方案是直接赋值: s 0 = q 0 , s n = q n s_{0}=q_{0},s_{n}=q_{n} s0=q0,sn=qn,当然也可以定义为其它值。 s 0 s_{0} s0和 s n s_{n} sn的选择对结果插值曲线影响较小,所以下面我们着重考虑应用细节的选择。
和Slerp插值曲线类似,为了实现应用的目的,有必要生成插值参数的离散值版本,并且选择确定每个关键帧之间的插值帧数量。对于Slerp来说,这个过程相对容易,因为插值曲线的圆弧长度和两个相关联的四元数之间的角度相关。然而Squad的插值曲线是椭圆的,并且每对关键帧之间的弧长难以计算,因此每对关键帧之间的插值帧数量难以明确。基于此,我们根据每对关键帧之间的距离决定它们之间的插值帧数量,它不是最优选择,但是是一种简单有效的探索式方法。
Squad的插值曲线和角速度图如下所示:

从上图可以看出,Squad的插值曲线相当“完美”,“完美”可以解读为插值曲线是连续且可微的,但这样说不是很准确(或说这条澄清说明本质上是模糊的),因为一条连续可微的曲线也可以包含任意个不受控的波折。Squad的方程还远不能清晰决定曲线的定量属性,因此我们希望有一种更具体的方法来定义插值曲线,但是本篇不再适合使用合理的猜想来推导出新的插值方法。然而,先前陈述的方法为开发出一个更通用的方法奠定了基础。
在下一篇中,我们将在数学和物理的层面上更进一步,继续探索一种更通用的方法方程。
6. 代码实现
本节Squad的实现代码和Slerp实现类似,已放在上一篇《四元数线性插值方法:LinEuler/LinMat/Lerp/Nlerp/Slerp》,请移步上一篇第6节的代码实现查看。
另外,在博客的资源部分,博主会上传从论文《Quaternions, Interpolation and Animation》的第一作者Erik B. Dam获取的第一首源码资料。由于时间有限,写本系列的文章耗费了太多精力,加上代码用到的库比较旧,所以博主没打算修改调试这部分代码,不过感兴趣想要一试的童鞋可以和博主一起讨论实现细节。
参考文献:
- 《视觉SLAM十四讲:从理论到实践》,高翔、张涛等著,中国工信出版社
- Quaternions, Interpolation and Animation
- 四元数与三维旋转
- 贝塞尔曲线简单介绍
- 详解样条曲线(上)(包含贝塞尔曲线)
- 怎样理解贝塞尔曲线,样条线和贝塞尔样条线
- B样条曲线
- 《非均匀有理B样条(第2版)》,2010年12月清华大学出版社出版,作者(美)皮尔、(美)特莱尔,译者赵罡、穆国旺、王拉柱。