84. 柱状图中最大的矩形(Java)
1 题目
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
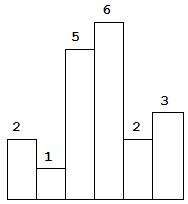
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
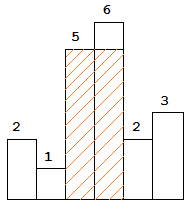
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
2 Java
2.1 方法一(分治,递归,比较快)
分治:
把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……
区域[left, right]内的最大面积由区域最小值决定(就是最小值 × 区域长度),按区域划分找各自区域内的最大面积,从这些结果中选出最大面积。
先以横轴最长[0, heights.length]为区域找最大面积(就是最小值 × 区域长度),再以最小值对应索引将区域分为左右两部分,分别计算着两部分区域的最大面积,递归
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights == null || heights.length == 0) return 0;
return calLargestSubRectangleArea(heights, 0, heights.length - 1);
}
// 用于计算区域[left, right]内的最大子矩形面积largestSubRectangleArea
public int calLargestSubRectangleArea(int[] heights, int left, int right){
if(left > right) return 0;
else{
int minValueIndex = findMinValueIndex(heights, left, right);
// 取max(当前最大面积,左最大面积,右最大面积),以区域[left, right]内最小值索引minValueIndex分左右,且不包括该索引
return Math.max(heights[minValueIndex] * (right - left + 1), Math.max(calLargestSubRectangleArea(heights, left, minValueIndex - 1), calLargestSubRectangleArea(heights, minValueIndex + 1, right)));
}
}
// 用于找区域[left, right]内最小值的索引minValueIndex
public int findMinValueIndex(int[] heights, int left, int right){
int minValueIndex = left;
for(int i = left; i <= right; i++){
if(heights[i] < heights[minValueIndex]) minValueIndex = i;
}
return minValueIndex;
}
}
化简后:
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights == null || heights.length == 0) return 0;
return calLargestSubRectangleArea(heights, 0, heights.length - 1);
}
// 用于计算区域[left, right]内的最大子矩形面积largestSubRectangleArea
public int calLargestSubRectangleArea(int[] heights, int left, int right){
if(left > right) return 0;
else{
// 找区域[left, right]内最小值的索引minValueIndex
int minValueIndex = left;
for(int i = left; i <= right; i++){
if(heights[i] < heights[minValueIndex]) minValueIndex = i;
}
// 取max(当前最大面积,左最大面积,右最大面积),以区域[left, right]内最小值索引minValueIndex分左右,且不包括该索引
return Math.max(heights[minValueIndex] * (right - left + 1), Math.max(calLargestSubRectangleArea(heights, left, minValueIndex - 1), calLargestSubRectangleArea(heights, minValueIndex + 1, right)));
}
}
}
2.2 方法二(暴力,慢)
遍历heights,计算以索引 i 为矩形左端的所有矩形面积,再将索引 i 不断向右移动直至结束
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights == null || heights.length == 0) return 0;
int largestRectangleArea = 0;
for(int i = 0; i < heights.length; i++){
largestRectangleArea = Math.max(largestRectangleArea, calLargestSubRectangleArea(heights, i, heights.length - 1));
}
return largestRectangleArea;
}
// 用于计算区域[left, right]内的最大子矩形面积largestSubRectangleArea
public int calLargestSubRectangleArea(int[] heights, int left, int right){
int largestSubRectangleArea = 0;
int minValue = heights[left];
for(int i = left; i <= right; i++){
if(heights[i] < minValue) minValue = heights[i];
largestSubRectangleArea = Math.max(largestSubRectangleArea, minValue * (i - left + 1));
}
return largestSubRectangleArea;
}
}
化简:
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights == null || heights.length == 0) return 0;
int largestSubRectangleArea = 0;
for(int i = 0; i < heights.length; i++){
int minValue = heights[i];
for(int j = i; j < heights.length; j++){
if(heights[j] < minValue) minValue = heights[j];
largestSubRectangleArea = Math.max(largestSubRectangleArea, minValue * (j - i + 1));
}
}
return largestSubRectangleArea;
}
}
2.3 方法三(栈,难,超快)
官方题解
public class Solution {
public int largestRectangleArea(int[] heights) {
Stack < Integer > stack = new Stack < > ();
stack.push(-1);
int maxarea = 0;
for (int i = 0; i < heights.length; ++i) {
while (stack.peek() != -1 && heights[stack.peek()] >= heights[i])
maxarea = Math.max(maxarea, heights[stack.pop()] * (i - stack.peek() - 1));
stack.push(i);
}
while (stack.peek() != -1)
maxarea = Math.max(maxarea, heights[stack.pop()] * (heights.length - stack.peek() -1));
return maxarea;
}
}