【Python】Apriori算法求解关联规则
文章目录
- 一、问题描述
- 二、实验思路
-
- 1、数据格式
- 2、频繁项集
-
- (1)连接步—产生候选式Ck
- (2)剪枝步—产生频繁项集Lk
- (3)输出结果
- 3、关联规则
-
- (1)计算方法
- (2)输出结果
- 三、完整代码
一、问题描述
某个商场的事务数据库D如表1所示,包括9个事务,即|D|=9。假设最小支持度min_sup=2,请使用Apriori算法找到D中的频繁项集,并输出所有的关联规则(实验编程语言不限)。
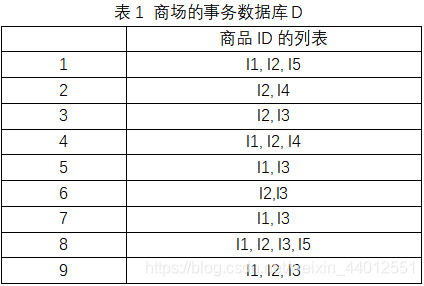
二、实验思路
1、数据格式
(1)想要得到类似于下图的表格输出,则需用到DataFrame,使用DataFrame则Lk、Ck集确定为字典的格式。

(2)由于DataFram是把字典的键作为列标签,若要让频繁项集一列、支持度计数一列,则需要进行转置。
print(pd.DataFrame(C, index=['支持度计数']).T)
(3)字典是无序的,Apriori算法需要字典是有序的,所以在计算每一项出现的次数之前,先把key按顺序排列好放入字典中。
以C1的处理为例:
# C1
C={
}
Lkey = []
for values in data['商品ID的列表']:
Lkey.extend(["{"+item+"}" for item in values if item not in Lkey])
Lkey.sort()# 整理键的顺序
for i in Lkey:
C[i]=0
for values in data['商品ID的列表']:
for item in values:
C["{"+item+"}"]+=1
"""
——————C1——————
支持度计数
{I1} 6
{I2} 7
{I3} 6
{I4} 2
{I5} 2
"""
(4)字典不是不支持列表吗?如果要生成如下图的效果怎么用字典实现?

强制类型转换,把列表转成字符串。同时增加对额外字符“{”、"}"的处理。
# 对额外字符的处理-删去
for key in L.keys():
key = key.replace('{','')
key = key.replace('}','')
Lstr.append(key)
Lkey.append(key.split(','))
# 对额外字符的处理-增加
Lkey_new.sort()# 整理键的顺序
for i in Lkey_new:
C["{"+i+"}"]=0
2、频繁项集
(1)连接步—产生候选式Ck

敲重点:
1)以集合 L 1 = L_1= L1={ {I1,I2},{I1,I3},{I1,I5},{I2,I3},{I2,I4},{I2,I5}}为例(下标从1开始数)
i) L L L是集合
{ {I1,I2},{I1,I3},{I1,I5},{I2,I3},{I2,I4},{I2,I5}}
ii) l i l_i li是集合L中的项集,如 l 1 = l_1= l1={I1,I2}、 l 2 = l_2= l2={I2,I5}
iii) l i [ j ] l_i[j] li[j]表示 l i l_i li的第 j j j项,如 l 1 [ 1 ] = l_1[1]= l1[1]=I1, l 4 [ 2 ] = l_4[2]= l4[2]=I3
iiii)前 k − 2 k-2 k−2个项相同等价于除了最后一个项以外其它项都相同。
如{I1,I2},{I1,I3},第一项相同,最后一项不同,合并为{I1,I2,I3}
如{I1,I2},{I2,I3},第一项不同,不进行合并,若合并则会与前面的项重复,这条规则是为了不产生重复项。
2)项按字典序排序,即{I1,I2}需放在{I1,I3}的前面,这步在二、1、数据格式中介绍过了。
# 产生候选C
def Apriori_gen(Lkey,Lstr):
# Lkey-字典L的key-列表/Lstr-字典L的key-字符串
# 连接步
C={
}
Lkey_new = []
for i in range(len(Lkey)-1):
j=i
flag = 0
for j in range(i+1,len(Lkey)):
# 检查Lkey[i]和Lkey[j]是否除最后一项外前面的几项都相同
for x in range(len(Lkey[i])):
if x==len(Lkey[i])-1:
if Lkey[i][x]==Lkey[j][x]:
print("ERROR:出现重复的频繁项")
print(Lkey[i])
print(Lkey[j])
exit(0)
else:
# 找到合并项集,加入
temp=Lstr[i]+','+str(Lkey[j][x])
# 若子集都是频繁项集,则加入到新的键表中
if not Has_infrequent_subset(temp,Lkey):
Lkey_new.append(temp)
# 若前k-2项出现不同,退出循环
elif Lkey[i][x]!=Lkey[j][x]:
flag=1
break
if flag==1:
break
# 整理键的顺序
Lkey_new.sort()
for i in Lkey_new:
C["{"+i+"}"]=0
return C
(2)剪枝步—产生频繁项集Lk
# 判断是否存在非频繁项集
def Has_infrequent_subset(candi_set,Lkey):
# candi_set-候选集、L_k-1的频繁集
candi_set = candi_set.split(',')
for x in candi_set:
subset = candi_set[:]
subset.remove(x)
if subset not in Lkey:
return True
return False
# 若子集都是频繁项集,则加入到新的键表中
if not Has_infrequent_subset(temp,Lkey):
Lkey_new.append(temp)
2)把小于最小支持度的频繁项集删除,即把大于等于最小支持度的频繁项集加入到L中
L = {
}
for key, values in C.items():
if values >= min_sup:
L[key] = values
(3)输出结果
——————Data——————
商品ID的列表
0 [I1, I2, I5]
1 [I2, I4]
2 [I2, I3]
3 [I1, I2, I4]
4 [I1, I3]
5 [I2, I3]
6 [I1, I3]
7 [I1, I2, I3, I5]
8 [I1, I2, I3]
——————C1——————
支持度计数
{
I1} 6
{
I2} 7
{
I3} 6
{
I4} 2
{
I5} 2
——————L1——————
支持度计数
{
I1} 6
{
I2} 7
{
I3} 6
{
I4} 2
{
I5} 2
——————C2——————
支持度计数
{
I1,I2} 4
{
I1,I3} 4
{
I1,I4} 1
{
I1,I5} 2
{
I2,I3} 4
{
I2,I4} 2
{
I2,I5} 2
{
I3,I4} 0
{
I3,I5} 1
{
I4,I5} 0
——————L2——————
支持度计数
{
I1,I2} 4
{
I1,I3} 4
{
I1,I5} 2
{
I2,I3} 4
{
I2,I4} 2
{
I2,I5} 2
——————C3——————
支持度计数
{
I1,I2,I3} 2
{
I1,I2,I5} 2
——————L3——————
支持度计数
{
I1,I2,I3} 2
{
I1,I2,I5} 2
3、关联规则
(1)计算方法
![]()


敲重点:
1)频繁项集 l l l是集合 T T T的子集,这里的集合 T T T即为上一步的结果 L L L。
2)如求解 A = > B A=>B A=>B的置信度,则先求数据库中 A ∪ B A\cup B A∪B的数目,再求数据库中 A A A的数目,做除法,结果为 A = > B A=>B A=>B的置信度。若大于最小置信度阈值则输出关联规则。
# 产生非空子集并计算关联度
def Non_subset(Lkey,D,min_conf):
# Lkey-频繁项集的集合、D-数据库、min_conf-最小置信度
conf={
}
for l in Lkey:
non_subset = []
# 获取频繁项集l的所有非空子集
for i in range(len(l)):
for j in combinations(l, i + 1):
non_subset.append(j)
# 对非空子集进行格式处理
non_subset_new = []
for i in non_subset:
temp = []
for j in i:
temp.append(j)
non_subset_new.append(temp)
# 产生关联规则/计算关联度
for i in range(len(non_subset_new)-1):
for j in range(i+1,len(non_subset_new)):
A = non_subset_new[i]
B = non_subset_new[j]
AB = list(set(A).union(set(B))) # 取并集
# 存在相同元素
if len(AB)!=len(A)+len(B):
continue
# 计算数目
A_cnt = Cul_itemcnt(D,A)
B_cnt = Cul_itemcnt(D,B)
AB_cnt = Cul_itemcnt(D,AB)
if len(A) == 1:
Astr = A[0]
else:
Astr = Conf_deal(A)
if len(B) == 1:
Bstr = B[0]
else:
Bstr = Conf_deal(B)
# 与最小置信度阈值比较
if AB_cnt/A_cnt>=min_conf:
s = Astr+"=>"+Bstr
s = s.replace("'","")
conf[s] = AB_cnt/A_cnt
if AB_cnt/B_cnt>=min_conf:
s = Bstr+"=>"+Astr
s = s.replace("'","")
conf[s] = AB_cnt/B_cnt
return conf
(2)输出结果
假定最小置信度阈值为0
置信度
I1=>I2 0.666667
I2=>I1 0.571429
I1=>I3 0.666667
I3=>I1 0.666667
I1=>{
I2, I3} 0.333333
{
I2, I3}=>I1 0.500000
I2=>I3 0.571429
I3=>I2 0.666667
I2=>{
I1, I3} 0.285714
{
I1, I3}=>I2 0.500000
I3=>{
I1, I2} 0.333333
{
I1, I2}=>I3 0.500000
I1=>I5 0.333333
I5=>I1 1.000000
I1=>{
I2, I5} 0.333333
{
I2, I5}=>I1 1.000000
I2=>I5 0.285714
I5=>I2 1.000000
I2=>{
I1, I5} 0.285714
{
I1, I5}=>I2 1.000000
I5=>{
I1, I2} 1.000000
{
I1, I2}=>I5 0.500000
三、完整代码
Apriori算法求解关联规则完整代码
