最小生成树与二分图

最小生成树

Prim算法

https://www.acwing.com/problem/content/860/

算法思想

维护一个集合，每次找到一条集合中点可以到达的最小的边，然后把这条边的终点记录在集合中，继续重复迭代，直到所有的点都选择完毕。

时间复杂度：因为是两层循环，所以说时间复杂度还是O(n2)。

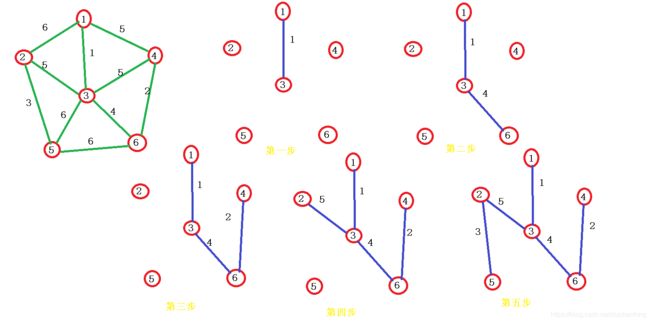
算法流程

源代码

#include 
#include 
#include 

using namespace std;

const int N = 510, M = 1e5 + 10, INF = 0x3f3f3f3f;
int dist[N], g[N][N];
bool vis[N];
int n,m;
int u,v,w;

int prim() {
     
    memset(dist, 0x3f, sizeof dist);
    
    int res = 0;
    for(int i = 0; i < n; i++) {
     
        
        int t = -1;
        for(int j = 1; j <= n; j++)
            if(!vis[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
                
        // 不连通的图，他的边权为 INF
        if(i && dist[t] == INF) return -1;
        if(i) res += dist[t];
        
        for(int j = 1; j <= n; j++)
            dist[j] = min(dist[j], g[t][j]);
        vis[t] = true;
    }
    
    return res;
}

int main() {
     
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    for(int i = 0; i < m; i++) {
     
        cin >> u >> v >> w;
        g[v][u] = g[u][v] = min(w, g[u][v]);  // 重边 & 无向图
    }
    
    int t = prim();
    
    if(t == -1) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

Kruskal算法

https://www.acwing.com/problem/content/861/

算法思想

首先先对所有的边从小到大排序，然后在保证没有回路的前提下选出权重较小的$n-1$条边，如果$(i，j)$是所有集合中没有选择的边中权重最小的，并且$(i，j)$不会和已选的边构成回路。如果$(i，j)$的两个 点 $i$ 和 $j$ 同属于一个连通分支，那么选择$i$ 和 $j$会构成回路，反之则不会。

连通分支

对于一个无向图而言，它的一个极大连通子图即为一连通支。比如说，一个图由三部分构成，其中每一部分都是连通的，但三个部分之间互相不连通，那么每一部分即为无向图的一个连通分支。此图的连通分支数为3。

时间复杂度：给每个边排序的时间复杂度为$O(n\ast logn)$，选择边的时候时间复杂度是$O(logn)$，所以说总的时间复杂度是$O(n\ast logn)$。

算法流程

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10, M = 2 * N;
int f[N];
int n,m;

struct node{
     
    int u,v,w;
    bool operator< (const node& t) const {
     
        return w < t.w;
    }
}e[M];

int find(int x) {
     
    if(x != f[x]) f[x] = find(f[x]);
    return f[x];
}

int kruskal() {
     
    sort(e, e + m);
    for(int i = 1; i <= n; i++) f[i] = i;   // 并查集初始化
    
    int res = 0, cnt = 0;
    for(int i = 0; i < m; i++) {
     
        int u = e[i].u, v = e[i].v, w = e[i].w;
        
        u = find(u);
        v = find(v);
        if(u != v) {
     
            f[u] = v;
            res += w;
            cnt ++;
        }
    }
    
    if(cnt != n - 1) return -1;
    return res;
}

int main() {
     
    cin >> n >> m;
    for(int i = 0; i < m; i++) {
     
        int u,v,w;
        cin >> u >> v >> w;
        e[i] = {
     u,v,w};
    }
    
    int t = kruskal();
    
    if(t == -1) puts("impossible");
    else cout << t << endl;
    return 0;
}

二分图

二分图，就是在一个图中，一定不含有奇数个节点的环；（不构成环的连通分支，是特殊的二分图）

二分图不一定要求是连通的，可以是几个连通图构成的

染色法

https://www.acwing.com/problem/content/description/862/

算法思路

将所有点分成两个集合，使得所有边只出现在集合之间

dfs

流程

1. 染色可以使用1和2区分不同颜色，用0表示未染色
2. 遍历所有点，每次将未染色的点进行dfs， 默认染成1或者2，算法中可以使用$3-c$
3. 由于某个点染色成功不代表整个图就是二分图,因此只有某个点染色失败才能立刻break/return，染色失败相当于至少存在2个点染了相同的颜色

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10, M = 2 * N;
int h[M], e[M], ne[M], idx;
int color[N];
int n,m;

void add(int u,int v) {
     
    e[idx] = v, ne[idx] = h[u], h[u] = idx++;
}

bool dfs(int u, int c) {
     
    color[u] = c;   // 当前节点染色为 c 颜色，那么他的下一个节点应该为 3-c 颜色  1,2
    
    for(int i = h[u]; ~i ; i = ne[i]) {
     
        int v = e[i];
        
        if(!color[v]) {
     
            if(!dfs(v, 3 - c)) return false;
        } else if(color[v] == c) {
           // 与下一个节点的染色出现矛盾
            return false;
        }
    }
    
    return true;
}

int main() {
     
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i++) {
     
        int u,v;
        cin >> u >> v;
        add(u,v), add(v,u);
    }
    
    bool flag = true;
    for(int i = 1; i <= n; i++) 
        if(!color[i])       // 当前节点没有染色
            if(!dfs(i,1)) {
      // 给当前节点染成1号色，然后遍历下面的分支
                flag = false;   // 出现矛盾，不是二分图
                break;
            }
    
    if(flag) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

bfs

算法流程

1. 颜色 1 和 2 表示不同颜色, 0 表示 未染色

2. 队列初始化将第i个点入队, 默认颜色可以是1或2
   

bool bfs(int u) {
     
    color[u] = 1;   // 当前节点染色为 c 颜色，那么他的下一个节点应该为 3-c 颜色  1,2
    queue<int> que;
    que.push(u);
    
    while(!que.empty()) {
     
        int size = que.size();
        while(size --) {
     
            int f = que.front();
            que.pop();
            
            for(int i = h[f]; ~i ; i = ne[i]) {
     
                int v = e[i];
                if(!color[v]) {
     
                    color[v] = 3 - color[f];
                    que.push(v);    
                } else if ( color[f] == color[v] ){
      // 与下一个节点的染色出现矛盾
                    return false;
                }
            }
        }
    }
    
    return true;
}

匈牙利法

https://www.acwing.com/problem/content/863/

算法描述

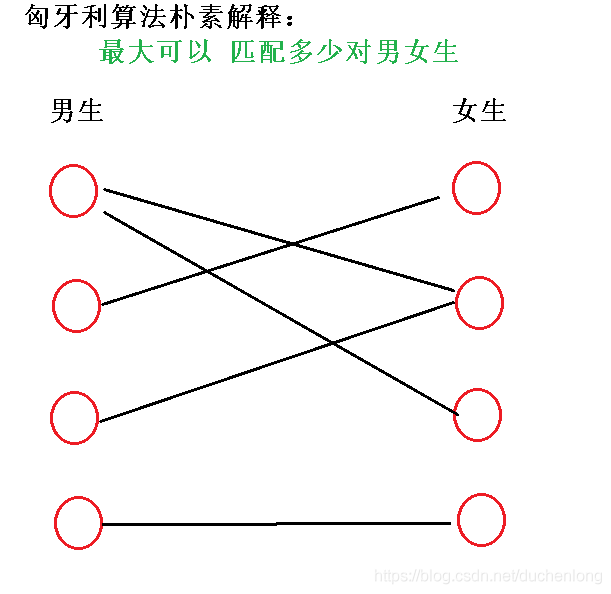
就是在一个二分图中，每个集合中的点只能用一次，问可以连多少条边

yxz人生导师的描述

两个集合，一个男生，一个女生。

已知每个男生钟意的女生编号，为尽量多的男生进行分配，hha

如果男生钟意的妹子已经有了男朋友，
你就去问问她男朋友，
你有没有备胎，
把这个让给我好吧

#include 
#include 
#include 

using namespace std;

const int N = 510, M = 1e5 + 10;
int h[N], e[M], ne[M], idx;
int match[N];   // 每一个右边对应的左边编号
bool vis[N];    // 当前右边是否被访问
int n1,n2,m;

void add(int u,int v) {
     
    e[idx] = v, ne[idx] = h[u], h[u] = idx++;
}

bool find(int u) {
     
    
    for(int i = h[u]; ~i ; i = ne[i]) {
     
        int v = e[i];
        if(!vis[v]) {
     
            vis[v] = true;
            // 当前访问的右边没有被绑定  或者  绑定的左边可以找到下一个不冲突的右边 进行更新
            if(match[v] == 0 || find(match[v])) {
     
                match[v] = u;
                return true;
            }
        }
    }
    
    return false;
}

int main() {
     
    cin >> n1 >> n2 >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i++) {
     
        int u,v;
        cin >> u >> v;
        add(u,v);
    }
    
    int res = 0;
    for(int i = 1; i <= n1; i++) {
     
        memset(vis, false, sizeof vis);
        if(find(i)) res ++; // 可以不冲突的分配
    }
    
    cout << res << endl;
    return 0;
}