Dijkstra模板(C语言)
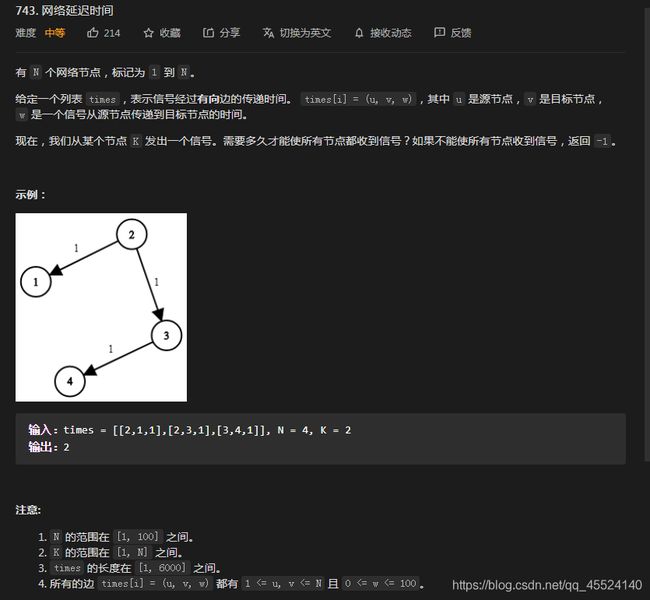
dijkstra的经典的单源最短路径算法,用于求解无负边权的最短(最长)路问题。主要特点是从起点开始,采用贪心方法的策略,每次遍历到离源点最近且未访问过的邻接节点,直到扩张到终点为止。
算法步骤:
1.初始化dist数组为INF(dist[i]表示源点到i的最短距离)
2.预处理,将dist[s]设为0,自己到自己的距离为0,且将s点与其邻接点的距离更新到dist数组中
3.从未收录的结点中选择距离最近结点的收录
4.将s点与收录点的所有未邻接点的距离更新(贪心)
朴素dijkstra
1.当图中节点较少(n <= 1000),边数(m)较多时,适合采用邻接表存图(如果用邻接矩阵存图,需要初始化为INF,表示两点不可达)
代码如下:
#include 2.当图的结点较多时,需要使用邻接表存图(由于指针表示的邻接表代码较多,这里用数组来模拟邻接表),使用邻接表不用担心重边问题,因为邻接边都会被更新到
代码如下:
#include 时间复杂度: O ( n m ) O(nm) O(nm)
堆优化的dijkstra
我们可以发现,dijkstra算法的第三步我们可以继续优化,不用每次都遍历n个结点,用堆这个数据构可以实现O(1)得到离源点距离最近的结点,O(logn)的时间复杂度插入结点,堆结点除了距离我们还要标识一下对应的结点标号,如果取出的点已经被收录,需要继续取结点
代码如下:
#include 时间复杂度: O ( m l o g n ) O(mlogn) O(mlogn)
例题:
参考代码(1):
结构体指针实现的邻接表
typedef struct LGraph LGraph;
struct LGraph{
int V;
int T;
LGraph* next;
};
//头插法插入邻接点
void InertVertex(LGraph* obj, int pos, int v, int time){
LGraph* tmp = (LGraph*)malloc(sizeof(LGraph));
tmp->V = v;
tmp->T = time;
tmp->next = obj[pos].next;
obj[pos].next = tmp;
}
//初始化邻接表
LGraph* BuildGraph(int NumVertex){
LGraph* obj = (LGraph*)calloc(NumVertex, sizeof(LGraph)); //结构体数组
for(int i = 0; i < NumVertex; i++){
obj[i].V = i;
obj[i].next = NULL;
}
return obj;
}
//返回未被收录顶点中dist最小者
int FindMinDist(int n, int* dist, bool* collected){
int MinDist = INT_MAX;
int MinV;
for(int i = 1; i < n; i++){
if(collected[i] == false && dist[i] < MinDist){
MinDist = dist[i];
MinV = i;
}
}
if(MinDist == INT_MAX) return -1;
else return MinV;
}
int networkDelayTime(int** times, int timesSize, int* timesColSize, int N, int K){
LGraph* graph = BuildGraph(N + 1);
for(int i = 0; i < timesSize; i++)
InertVertex(graph, times[i][0], times[i][1], times[i][2]);
int* dist = (int*)calloc(N + 1, sizeof(int));
for(int i = 0; i < N + 1; i++) dist[i] = INT_MAX;
bool* collected = (bool*)calloc(N + 1, sizeof(bool));
memset(collected, 0, (N + 1) * sizeof(bool));
//对dist数组进行预处理
LGraph* p = (&graph[K])->next;
while(p != NULL){
dist[p->V] = p->T;
p = p->next;
}
//起点收入集合
dist[K] = 0;
collected[K] = true;
//Dijkstra算法
while(1){
int v = FindMinDist(N + 1, dist, collected);
if(v == -1) break;
collected[v] = true;
p = (&graph[v])->next;
while(p != NULL){
if(collected[p->V] == false && dist[v] + p->T < dist[p->V])
dist[p->V] = dist[v] + p->T;
p = p->next;
}
}
//遍历dist数组,若无未访问的节点,返回最大值
int delaytime = -1;
for(int i = 1; i < N + 1; i++){
if(dist[i] == INT_MAX){
delaytime = -1;
break;
}
else delaytime = delaytime < dist[i] ? dist[i] : delaytime;
}
//释放内存
free(graph);
free(dist);
free(collected);
return delaytime;
}
参考代码(2):
邻接矩阵实现
int n;
#define MAXN 105
const int INF = 0x3f;
int g[MAXN][MAXN], dist[MAXN];
bool st[MAXN];
void dijkstra(int s){
for(int i = 1; i <= n; i++) dist[i] = g[s][i];
dist[s] = 0;
st[s] = true;
int v = s;
for(int i = 1; i <= n; i++){
int mind = 0x3f3f3f3f;
for(int j = 1; j <= n; j++){
if(!st[j] && dist[j] < mind){
mind = dist[j];
v = j;
}
}
st[v] = true;
for(int j = 1; j <= n; j++){
if(dist[v] + g[v][j] < dist[j])
dist[j] = dist[v] + g[v][j];
}
}
}
int networkDelayTime(int** times, int timesSize, int* timesColSize, int N, int K){
int u, v, w;
n = N;
memset(g, INF, sizeof(g));
memset(dist, INF, sizeof(dist));
memset(st, false, sizeof(st));
for(int i = 0; i < timesSize; i++){
u = times[i][0], v = times[i][1], w = times[i][2];
g[u][v] = w;
}
dijkstra(K);
int res = 0;
for(int i = 1; i <= N; i++){
if(dist[i] == 0x3f3f3f3f)
return -1;
else res = fmax(res, dist[i]);
}
return res;
}
2.LeetCode 1514.概率最大的路径
此题相当于是求最长路,且需要堆优化
参考代码:
//dijkstra + 堆优化
#define N 10010
#define M 100000
int h[N], to[M], ne[M], idx;
double w[M], dist[N], heap[M][2];
int heapSize;
int hv; //出堆结点标号
double hp; //源点到出堆结点的最大概率
bool st[N];
void push(int v, double p){
int i;
for(i = ++heapSize; heap[i / 2][0] < p; i /= 2){
heap[i][0] = heap[i / 2][0];
heap[i][1] = heap[i / 2][1];
}
heap[i][0] = p;
heap[i][1] = v;
}
void pop(){
hp = heap[1][0];
hv = heap[1][1];
double lastp = heap[heapSize][0];
int lastv = heap[heapSize--][1];
int i, child;
for(i = 1; i * 2 <= heapSize; i = child){
child = i * 2;
if(child != heapSize && heap[child + 1][0] > heap[child][0]) child++;
if(lastp < heap[child][0]){
heap[i][0] = heap[child][0];
heap[i][1] = heap[child][1];
}
else break;
}
heap[i][0] = lastp;
heap[i][1] = lastv;
}
void add(int a, int b, double c){
to[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void dijkstra(int s, int n){
dist[s] = 1.0;
push(s, 1.0);
while(heapSize > 0){
pop();
if(st[hv]) continue;
st[hv] = true;
for(int i = h[hv]; ~i; i = ne[i]){
if(!st[to[i]] && hp * w[i] > dist[to[i]]){
dist[to[i]] = hp * w[i];
push(to[i], dist[to[i]]);
}
}
}
}
double maxProbability(int n, int** edges, int edgesSize, int* edgesColSize, double* succProb, int succProbSize, int start, int end){
int a, b;
double c;
idx = heapSize = 0;
heap[0][0] = 1.0; //哨兵结点
memset(st, false, sizeof(st));
memset(h, -1, sizeof(h));
for(int i = 0; i < n; i++) dist[i] = 0.0;
for(int i = 0; i < edgesSize; i++){
a = edges[i][0], b = edges[i][1], c = succProb[i];
add(a, b, c);
add(b, a, c);
}
dijkstra(start, n);
if(dist[end] == 0.0) return 0.0;
return dist[end];
}