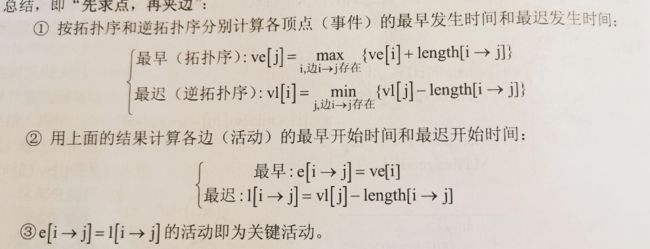algorithm
[摘自算法笔记]
全排列问题
求 1- n的全排列
generateP(int index); 假设当前已经填好了p[1]~p[index - 1],正准备向p[index]位置填入数字。显然需要枚举1~n填入,但是需要当前数字x不在p[1] ~ p[index-1]中,所以就需要通过hashTable[x]==false来判断。如果可以填入,则p[index]=x,并将hashTable[x]=true; 然后通过递归处理index+1位。递归结果后需要设置hashTable[x]=false。
递归边界:index == n + 1 表示前面 1~ index 已经填好数据。
public class MyTest {
//举个例子,求123的全排列
int[] p = new int[11];
boolean[] hasTable = new boolean[11];//这个数组可以使用map代替
int n;
//当前处理到第index号位,默认 1~index-1 已经放好数字了
void generateP(int index){
if(index == n ){
for (int i = 0; i < n ; i++) {
System.out.print(p[i]);
}
System.out.println();
return;
}
// for (int x = 0; x < n; x ++){ //求0到n-1的全排列
for (int x = 1; x <= n; x ++){
if(hasTable[x] == false){
//如果x不在 p[1]~p[index]之中
p[index] = x;
hasTable[x] = true;
generateP(index + 1);
hasTable[x] = false;//x放到index位已经处理完,还原状态,这样x可以放到index+1之后的位置了
}
}
}
@Test
public void test(){
n = 3;
generateP(0);
}
}
n皇后问题(leetcode 51)
https://leetcode-cn.com/problems/n-queens/
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
输入:4
输出:[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
package perday;
import org.junit.Test;
import java.util.ArrayList;
import java.util.List;
public class LeetCode51 {
List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
N = n;
p = new int[N];
hashTable = new boolean[N];
for (int i = 0; i < N; i++) {
st += ".";
}
generateP(0);
return res;
}
String st = "";
//每行都有一个皇后,index代表第index行的皇后,
int[] p;//p[index]代表 index行的那个皇后所在的列数
boolean[] hashTable;
//假设1 ~ index - 1 的皇后已经排好了,并且没有冲突
int N;// N 个皇后
int count = 0;
void generateP(int index){
if(index == N){
//
count ++;
List<String> tmp = new ArrayList<>(N + 1);
for (int i = 0; i < N; i++) {
StringBuilder str = new StringBuilder(st);
str.setCharAt(p[i],'Q');
tmp.add(str.toString());
}
res.add(tmp);
return;
}
for (int x = 0; x < N; x ++){
if(hashTable[x] == false){
boolean flag = true; //表示第index行的皇后放到x位置不会有冲突
for(int i = 0; i < index; i ++){
if(Math.abs(index - i) == Math.abs(x - p[i])){
//在对角线上了,有冲突
flag = false;
break;
}
}
if(flag){
//没有冲突才进行递归
hashTable[x] = true;
p[index] = x;
generateP(index + 1);
hashTable[x] = false;
}
}
}
}
@Test
public void test(){
System.out.println(solveNQueens(4));
System.out.println(count);
}
}
n皇后问题2(leetcode 52)
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
同上。
二分查找
package perday;
import org.junit.Test;
public class MyTest {
//返回x对应的下标
//查找的二分区间为[left, right],
int binarySearch(int[] a, int left, int right, int x){
int mid;
while(left <= right){
mid = (left + right) / 2;
if(a[mid] == x){
//查找成功
return mid;
}
if(a[mid] > x){
//x在[left, mid)
right = mid - 1;
}else {
left = mid + 1;
}
}
return -1;
}
@Test
public void test(){
int[] a = {
1,2,4,5,6,9,10};
System.out.println(binarySearch(a, 0, a.length-1, 2));//1
System.out.println(binarySearch(a, 0, a.length-1, 6));//4
System.out.println(binarySearch(a, 0, a.length-1, 7));//-1
}
}
Deformation
lower_bound
在A中找到第一个大于等于x的位置
package perday;
import org.junit.Test;
import java.util.Hashtable;
/**
* @author TylerChen
* @date 2020/12/12 - 12:19
*/
public class MyTest {
int lowerBound(int[] a, int left, int right, int x){
int mid;
while(left < right){
mid = (left + right) / 2;
if(a[mid] >= x){
//第一个大于等于x的数还有可能在左边
right = mid;//
}else {
left = mid + 1;
}
}
return left;
}
@Test
public void test(){
int[] a = {
1,1,2,2,5,5};
//如果这个数存在,则找到的是第一个满足条件的数的下标
System.out.println(lowerBound(a, 0, a.length, 1));//0
//如果这个数不存在,则返回这个数应该插入的位置
System.out.println(lowerBound(a, 0, a.length, 4));
System.out.println(lowerBound(a, 0, a.length, 0));
System.out.println(lowerBound(a, 0, a.length, 6));
}
}
模板:解决“寻找有序序列第一个满足条件的元素的位置”问题的模板
int solve(int[] a, int left, int right, int x){
int mid;
while(left < right){
mid = (left + right) / 2;
if(条件){
//第一个满足条件的位置还有可能在左边
right = mid;//
}else {
left = mid + 1;
}
}
return left;
}
如果要寻找最后一个满足条件C元素的位置,可以先求第一个满足条件!C的位置,然后再将这个位置减一即可。
计算右侧小于当前元素的个数 (leetcode 315)
https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
思路:使用二分法,否则会超时。
从最后一个元素x开始,找其右侧元素集合中小于x的个数,其右侧集合用temp表示,最后一个寻找完毕之后,将x加入temp中,以供倒数第二个元素查找。
查找时使用二分法,这样也可以顺便得到 查找元素应该在temp中的位置, 这样使用temp.add就可以将对应元素加入,得到的temp仍然是一个有序的序列。
class Solution {
public List<Integer> countSmaller(int[] nums) {
List<Integer> res = new ArrayList<>(nums.length + 1);
//每次都从temp中查找符合条件的元素
List<Integer> temp = new ArrayList<>();
for (int i = nums.length - 1; i >= 0; i--) {
int index = lowerBound(temp, nums[i]);
res.add(index);
temp.add(index, nums[i]);
}
Collections.reverse(res);
return res;
}
//找到第一个满足 >= x的下标,也就是x应该在temp中的位置,还是
int lowerBound(List<Integer> list, int x) {
int left = 0, right = list.size();
while (left < right) {
int mid = (left + right) / 2;
if (list.get(mid) >= x) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}
排序
归并排序
将序列两两分组,组内单独排序,然后再将这些组合并
首先是两个有序区间的合并
//将数组[l1,r1]与[l2,r2]区间合并为有序区间(此处l2即为r1+1)
void merge(int[] a, int l1, int r1, int l2, int r2){
int i = l1, j = l2;
int[] temp = new int[a.length];
int index = 0;
while (i <= r1 && j <= r2){
if(a[i] <= a[j]){
//将小的加入到temp[index]
temp[index ++] = a[i ++];
}else {
temp[index ++] = a[j ++];
}
}
while (i <= r1){
temp[index ++] = a[i ++]; //可能会有剩余
}
while (j <= r2){
temp[index ++] = a[j ++];
}
//将temp中的排好序的元素赋值给a
for (i = 0; i < index; i ++){
a[l1 + i] = temp[i];
}
}
递归实现
public class MyTest {
//在当前区间[left, right]进行归并排序
void mergeSort(int a[], int left, int right){
if(left < right){
int mid = (left + right) / 2;
mergeSort(a, left, mid);
mergeSort(a, mid + 1, right);
merge(a, left, mid, mid + 1, right);
}
}
@Test
public void test(){
int[] a = {
1,2,7,3,5,9,-1,0,12,11};
mergeSort(a, 0, a.length - 1);
System.out.println(Arrays.toString(a));
}
}
非递归实现
void mergeSort(int[] a) {
//step 为组内元素的个数,step / 2 为左子区间元素的个数
for (int step = 2; step < a.length; step *= 2) {
for (int i = 0; i < a.length; i += step) {
int mid = i + step / 2 - 1;
if (mid + 1 < a.length) {
merge(a, i, mid, mid + 1, Math.min(i + step - 1, a.length - 1));
}
}
}
}
快速排序
第一轮,a[] , left = 0, right = a.length - 1
令 a[left]为主元,从right开始,如果a[right] > 主元,则right --; 等循环结束,a[right] <= 主元,将a[right]中的元素放到a[left]中。如果a[left] <= 主元,则left ++; 等循环结束 a[left] > 主元,然后将a[right] = a[left];反复上面过程。结束后,中间剩余的那个位置就是主元应该在的位置,左边的元素都比它小,右边的都比他大。
package perday;
import org.junit.Test;
import java.util.Arrays;
import java.util.Hashtable;
/**
* @author TylerChen
* @date 2020/12/12 - 12:19
*/
public class MyTest {
//对区间进行划分,返回主元应该的位置
int partation(int[] a, int left, int right) {
int temp = a[left];//a[left]为主元
while (left < right) {
//把小于等于主元的元素,换到左边
while (left < right && a[right] > temp) {
right--;
}
a[left] = a[right];
//把大于主元的元素,换到左边
while (left < right && a[left] <= temp) {
left++;
}
a[right] = a[left];
}
a[left] = temp;
return left;
}
void quickSort(int a[], int left, int right) {
if (left < right) {
int pos = partation(a, left, right);
quickSort(a, left, pos - 1);
quickSort(a, pos + 1, right);
}
}
void quickSort(int a[]) {
quickSort(a, 0, a.length - 1);
}
@Test
public void test() {
int[] a = {
1, 2, 7, 3, 5, 9, -1, 0, 12, 11};
quickSort(a);
System.out.println(Arrays.toString(a));
}
}
数学问题
最大公约数
辗转相除法(欧几里得算法):两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。设a,b均为正整数,则gcd(a,b)=gcd(b,a%b)
int gcd(int a, int b){
//a为较大的那个数
int temp = Math.max(a, b);
a = temp;
b = a + b - temp;
while (a % b != 0){
int c = a % b;
a = b;
b = c;
}
return b;
}
//使用递归
int gcd2(int a, int b){
if(b == 0){
return a;
}else {
return gcd(b, a % b);
}
}
最小公倍数
a, b的最小公倍数为:a * b / gcd(a,b);
分数的四则运算
分数的表示:
class Fraction {
int up,down;
}
规则:
- down为非负数。如果down为负数,那么令up为负数。
- 如果改分数为0,规定其分子为0,分母为1。
- 分子和分母没有除了1以外的公约数。
分时的化简,以及四则运算:
package perday;
/**
* @author TylerChen
* @date 2020/12/13 - 14:31
*/
public class Fraction {
int up, down;
Fraction(int up, int down){
this.up = up;
this.down = down;
}
Fraction(){
};
int gcd(int a, int b){
int temp = Math.max(a, b);
a = temp;
b = a + b - temp;
while (a % b != 0){
int c = a % b;
a = b;
b = c;
}
return b;
}
//分式化简
//按照上面的规则,进行化简
Fraction reduction(Fraction res){
if(res.down < 0){
res.up = -res.up;
res.down = -res.down;
}
if(res.up == 0){
res.down = 1;
}else {
int d = gcd(Math.abs(res.up), Math.abs(res.down));
res.up /= d;
res.down /= down;
}
return new Fraction(res.up,res.down);
}
//加法 a/b + c/d = (ad + bc)/bd
Fraction add(Fraction f1, Fraction f2){
Fraction res = new Fraction();
res.up = f1.up * f2.down + f2.up * f1.down;
res.down = f1.down * f2.down;
return reduction(res);
}
//减法,乘法,除法略。
}
素数
素数:除了1和本身以外不能被其他数整除的数
素数的判断
boolean isPrime(int a){
if(a <= 1) {
return false;
}
int sqrt = (int) Math.sqrt(a);
for (int i = 0; i <= sqrt; i++) {
if(a % i == 0){
return false;
}
}
return true;
}
如果k是a的因子,那么a/k, 也是a的因子,并且 k 和 a/k 一个大于等于sqrt(a),另外一个小于等于sqrt(a);也就是说,在sqrt(a) 两边,如果有因子,则一定是成对出现的,所以只需要遍历到sqrt(a)即可。时间复杂度为O(logn)
获取素数表
Eratosthenes筛选法,时间复杂度O(nloglogn)
只需要确定2是素数即可,例如求1~15的素数
2是素数,2的倍数都不是素数,所以剩下的数为
2 3 5 7 9 11 13 15
3没有被筛选掉,所以3也是素数,把3的倍数都去掉
2 3 5 7 11 13
5 没有被筛选掉,所以5也是素数,把5的倍数筛选掉。
。。。。。
最终可以得到一个素数表
2 3 5 7 11 13
public class MyTest {
//寻找1 ~ n的素数表
List<Integer> findPrime(int n){
//flag[index] = false,代表index是宿舍,假设初始全都是素数
//默认2是素数
boolean[] flag = new boolean[n + 1];
List<Integer> res = new ArrayList<>();
for (int i = 2; i <= n; i ++){
if(flag[i] == false){
res.add(i);
for (int j = i + i; j <= n ; j += i) {
flag[j] = true;
}
}
}
return res;
}
@Test
public void test(){
System.out.println(findPrime(15));
}
}
质因子分解
所谓质因子就是将一个正整数n写成一个或者多个质数的乘积的形式,如6=2*3, 8=2*2*2
**结论:**对于一个正数n,如果它存在[2, n]范围内的质因子,要么这些质因子全部小于等于sqrt(n),要么只有一个大于sqrt(n),(如果有2个,那么相乘之后就大于n了)
思路:1,枚举1~sqrt(n)范围内的所有质因子p,判断p是否为n的因子,如果是,则令n/=p,直到p不是n的质因子为止。n/=p的次数,就是质因子p的个数。
2,如果经过步骤1 n仍然大于1,则说明n,有且仅有一个大于sqrt(n)的质因子,就是此时的n。
package perday;
import org.junit.Test;
import java.util.ArrayList;
import java.util.List;
/**
* @author TylerChen
* @date 2020/12/13 - 15:19
*/
public class Factor {
static class Fac{
int x;//质因子
int count;//质因子对应的个数
}
Fac[] fac = new Fac[10];
//考虑到2*3*5*7*11*13*17*19*23*29就超过int范围,所以,数组开到10就可以了
int num = 0;
//寻找某个数的质因子
void findFac(int n){
System.out.print(n + " = ");
num = 0;
List<Integer> prime = findPrime(20);
int sqrt = (int) Math.sqrt(n);
for (Integer p : prime){
if(n % p == 0){
fac[num] = new Fac();
fac[num].x = p;
fac[num].count = 0;
while (n % p == 0){
n /= p;
fac[num].count ++;
}
num ++;
}
}
if(n != 1){
fac[num] = new Fac();
fac[num].x = n;
fac[num].count = 1;
num ++;
}
printFac();
}
void printFac(){
for (int i = 0; i < num; i++) {
System.out.print(fac[i].x + "^" + fac[i].count);
if(i != num - 1){
System.out.print(" * ");
}
}
}
//寻找素数表
List<Integer> findPrime(int n){
boolean[] flag = new boolean[n + 1];
List<Integer> res = new ArrayList<>();
for (int i = 2; i <= n ; i++) {
if(flag[i] == false){
res.add(i);
for (int j = i * i;j <= n; j += i){
flag[j] = true;
}
}
}
return res;
}
@Test
public void test(){
findFac(180);//180 = 2^2 * 3^2 * 5^1
}
}
大整数运算
存储
// 如123456 则d[0]=6 d[1]=5
int[] d = new int[1000];
int len;
比较大小
- 如果两个bigint长度不相同,则长的大。
- 相同则从高位往到低位进行比较,出现某位不相等则可以判断大小。
- 遍历完还没有比较出来大小,则相等
四则运算
注意:这里的四则运算都是对于正整数而言的,如果是负数,可以处理完了再用四则运算,然后在处理一下
和小学列式子计算式一样的,需要有一个进位。
这种写法式对于两个对象都是正数而言的,如果一个数是负数,则可以使用高精度减法。如果都是负数,则去掉➖相加后再加上负号。
//高精度加法/
//和小学算加法一样
public static MyBigInt add(MyBigInt a, MyBigInt b){
MyBigInt res = new MyBigInt();
int carry = 0;//carry 是进位
for(int i = 0; i < a.len || i < b.len; i ++){
int temp = a.d[i] + b.d[i] + carry;
res.d[res.len ++] = temp % 10;
carry = temp / 10;
}
//如果最后进位不为0,则直接赋值给结果最高的那一位
if(carry != 0){
res.d[res.len ++] = carry;
}
return res;
}
乘法 高精度147 乘以 35
除法
**归纳:**上一步的余数除以10加上该步的位,得到该步临时的被除数,将其与除数比较:如果不够除,则改位的商位0;如果够除,则上即为对应的上,余数为对应的余数。最后要注意,减去高位可能有多余的0
完整代码
package perday;
import org.junit.Test;
import java.util.Arrays;
/**
* @author TylerChen
* @date 2020/12/14 - 10:02
*/
public class MyBigInt implements Comparable<MyBigInt> {
int[] d = new int[1000];
int len;
public MyBigInt() {
}
public MyBigInt(String str) {
this.len = str.length();
for (int i = 0; i < str.length(); i++) {
this.d[i] = str.charAt(str.length() - i - 1) - '0';
}
}
//通过string获取大整数
// 如123456 则d[0]=6 d[1]=5
MyBigInt getByStr(String str) {
MyBigInt big = new MyBigInt();
big.len = str.length();
for (int i = 0; i < str.length(); i++) {
big.d[i] = str.charAt(str.length() - i - 1);
}
return big;
}
@Override
public int compareTo(MyBigInt o) {
if (this.len > o.len) {
return 1;
} else if (this.len < o.len) {
return -1;
} else {
for (int i = this.len - 1; i >= 0; i--) {
if (this.d[i] > o.d[i]) {
return 1;
} else if (this.d[i] < o.d[i]) {
return -1;
}
}
}
return 0;
}
//高精度加法/
//和小学算加法一样
public static MyBigInt add(MyBigInt a, MyBigInt b) {
MyBigInt res = new MyBigInt();
int carry = 0;//carry 是进位
for (int i = 0; i < a.len || i < b.len; i++) {
int temp = a.d[i] + b.d[i] + carry;
res.d[res.len++] = temp % 10;
carry = temp / 10;
}
//如果最后进位不为0,则直接赋值给结果最高的那一位
if (carry != 0) {
res.d[res.len++] = carry;
}
return res;
}
//对于减法,a一定要比b大,
public static MyBigInt sub(MyBigInt a, MyBigInt b) {
MyBigInt res = new MyBigInt();
for (int i = 0; i < a.len || i < b.len; i++) {
if (a.d[i] < b.d[i]) {
//不够减需要向高位借位
a.d[i + 1]--;
a.d[i] += 10;//借1当10
}
res.d[res.len++] = a.d[i] - b.d[i];
}
//去掉高位的0;
while (res.len - 1 >= 1 && res.d[res.len - 1] == 0) {
res.len--;
}
return res;
}
//高精度与低精度的乘法
public static MyBigInt muti(MyBigInt a, int b) {
MyBigInt res = new MyBigInt();
int carry = 0;
for (int i = 0; i < a.len; i++) {
int temp = a.d[i] * b + carry;
//个位作为改位的结果
res.d[res.len++] = temp % 10;
//高位作为进位
carry = temp /= 10;
}
//和加法不一样,乘法的进位可能不止一位,
while (carry != 0) {
res.d[res.len++] = carry % 10;
carry /= 10;
}
return res;
}
public static MyBigInt divide(MyBigInt a, int b) {
int r = 0;
MyBigInt res = new MyBigInt();
res.len = a.len;
for (int i = a.len - 1; i >= 0; i--) {
r = r * 10 + a.d[i];
if(r < b){
//不够除
res.d[i] = 0;
}else {
res.d[i] = r / b;
r = r % b;
}
}
while (res.len - 1 >= 1 && res.d[res.len - 1] == 0){
res.len --;
}
return res;
}
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
for (int i = len - 1; i >= 0; i--) {
stringBuilder.append(d[i]);
}
return stringBuilder.toString();
}
public static void main(String[] args) {
MyBigInt a1 = new MyBigInt("123");
MyBigInt a2 = new MyBigInt("458");
MyBigInt a3 = new MyBigInt("121");
MyBigInt a4 = new MyBigInt("102");
MyBigInt[] aa = {
a1, a2, a3, a4};
Arrays.sort(aa);
System.out.println(Arrays.toString(aa));//[102, 121, 123, 458]
System.out.println(add(a1, a4));//225
System.out.println(sub(a1, a4));//21
System.out.println(muti(a1, 2));//246
System.out.println(divide(a1, 6));//20
}
}
搜索专题
DFS 深度优先搜索
问题:给定n个整数,从中选选择k个数,使得这k个数之和恰好等于一个给定的数x;如果有多种方案,选择他们中元素平方和最大的一个。例如:从{2,3,3,4}中选择2个数,使得他们的和为6,显然有2中方案{2,4}与{3,3},其中平方和最大的方案为{2,4};
package perday;
import org.junit.Test;
import java.util.ArrayList;
import java.util.List;
public class MyTest {
//从n个数中选择k个数使得和为x,最大平方和为maxSumSqu
int n = 4, k = 2, x = 6, maxSumSqu = -1;
int[] a = {
2, 3, 3, 4};
ArrayList<Integer> temp = new ArrayList<>(), ans = new ArrayList<>();
/**
* @param index 当前处理的整数编号
* @param nowK 已经选择数的个数
* @param sum 选择整数和
* @param sumSeq 平方和
*/
void DFS(int index, int nowK, int sum, int sumSeq) {
if(nowK == k && sum == x){
if(sumSeq > maxSumSqu){
maxSumSqu = sumSeq;
ans = new ArrayList<>(temp); //更新最优方案
}
return;
}
if(index == n || nowK > k || sum > x){
return;
}
//选择index号的数
temp.add(a[index]);
DFS(index + 1, nowK + 1, sum + a[index], sumSeq + a[index] * a[index]);
//不选index号的数
temp.remove(temp.size() - 1);
DFS(index + 1, nowK, sum , sumSeq);
}
@Test
public void test(){
DFS(0, 0, 0, 0);
System.out.println(ans);
}
}
修改题目为:假设N个整数中的每一个数都可以被选择多次。
这个问题只需要对原来的代码进行少量的修改即可。由于每个整数都可以被选择多次,因此当选择了index号数时,不应该直接进入index+1号数的处理。显然,应当能够继续选择index号的数,因此只需要把“选择index号数”这条分支的代码修改为DFS(index + 1, nowK + 1, sum + a[index], sumSeq + a[index] * a[index]);即可
BFS 广度优先搜索
广度优先遍历一般使用队列来实现,基本写法如下模板:
void BFS(T s){
Queue<T> q;
q.push(s);
设置为已入队;
while(!q.isEmpty()){
取出队首元素;
访问;
队首元素出队;
top的下一层节点未曾入队列的节点全部入队列,并设置为已入队;
}
}
例题:给出一个m*n的矩阵,矩阵中的元素为0或1.称位置(x,y)与其上下左右四个位置相邻。如果矩阵中有若干个1是相邻的(不必两两相邻),那么称这些1构成了一个“块”。求给定矩阵中块的个数。
{0,1,1,1,0,0,1},
{0,0,1,0,0,0,0},
{0,0,0,0,1,0,0},
{0,0,0,1,1,1,0},
{1,1,1,0,1,0,0},
{1,1,1,1,0,0,0}
//对于这个矩阵,块数为4
package perday;
import org.junit.Test;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class MyTest {
static class Node {
int x, y;
Node(int xx, int yy) {
x = xx;
y = yy;
}
}
int[][] matrix = {
{
0, 1, 1, 1, 0, 0, 1},
{
0, 0, 1, 0, 0, 0, 0},
{
0, 0, 0, 0, 1, 0, 0},
{
0, 0, 0, 1, 1, 1, 0},
{
1, 1, 1, 0, 1, 0, 0},
{
1, 1, 1, 1, 0, 0, 0}
};
boolean[][] inq = new boolean[6][7];
int m = 6, n = 7;// m * n的矩阵
int[] X = {
0, 0, 1, -1};
int[] Y = {
1, -1, 0, 0};
//判断某个坐标是否需要判断
//1,越界 2,当前位置已经进入过队列 3,当前位置是0 不是 1
boolean judge(int x, int y) {
if (x >= m || y >= n || x < 0 || y < 0) {
return false;
}
if (matrix[x][y] == 0 || inq[x][y]) {
return false;
}
return true;
}
void BFS(int x, int y) {
Queue<Node> q = new LinkedList<>();
Node a = new Node(x, y);
q.offer(a);
inq[x][y] = true;
while (!q.isEmpty()) {
Node p = q.poll();
for (int i = 0; i < X.length; i++) {
int newX = p.x + X[i];
int newY = p.y + Y[i];
if (judge(newX, newY)) {
q.offer(new Node(newX, newY));
inq[newX][newY] = true;
}
}
}
}
@Test
public void test() {
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 1 && inq[i][j] == false) {
ans++;
BFS(i, j);
}
}
}
System.out.println(ans);//
}
}
树
二叉树
根据先跟和中跟创建二叉树
结论:中序序列可以与先序序列、后序序列、层次序列中的任意一个来构建唯一的二叉树。而后者两两搭配或是三个一起都无法构建唯一的二叉树。 原因是先序、后序、层次均是提供根节点,作用是相同的,都必须由中序序列来区分出左右子树。
先中后根遍历、层次遍历
package perday;
import org.junit.Test;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Map;
import java.util.Queue;
public class BinaryTree {
static class Node {
int data;
int layer;//该节点所在的层次
Node left, right;
}
//根据先根和后跟创建一棵二叉树
int[] pre, inOr;
Map<Integer, Integer> inOrToIndex = new HashMap<>();
Node create(int[] pre, int[] inOr) {
this.pre = pre;
this.inOr = inOr;
for (int i = 0; i < inOr.length; i++) {
inOrToIndex.put(inOr[i], i);
}
return create(0, pre.length - 1, 0, inOr.length - 1);
}
Node create(int preL, int preR, int inL, int inR) {
if (preL > preR) {
//如果先序长度小于等于0,直接返回
return null;
}
Node root = new Node();
root.data = pre[preL];//
//获得先跟第一个节点在后跟中的位置
int k = inOrToIndex.get(pre[preL]);
//所以当前root左子树的节点个数为
int numLeft = k - inL;
//左子树的先序区间为 [preL, preL + numLeft] 中序区间为
root.left = create(preL + 1, preL + numLeft, inL, k - 1);
//右子树的先序区间为[preL+numLeft + 1,preR] 中序区间为[k + 1,inR]
root.right = create(preL + numLeft + 1, preR, k + 1, inR);
return root;
}
void preOrder(Node root){
if(root == null){
return;
}
System.out.print(root.data + " ");
preOrder(root.left);
preOrder(root.right);
}
void inOrder(Node root){
if(root == null){
return;
}
inOrder(root.left);
System.out.print(root.data + " ");
inOrder(root.right);
}
void postOrder(Node root){
if(root == null){
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data + " ");
}
void layerOrder(Node root){
Queue<Node> q = new LinkedList<>();
q.offer(root);
root.layer = 1;
while (!q.isEmpty()){
Node p = q.poll();
System.out.print(p.data + "(" + p.layer + ")" + " ");
if(p.left != null){
p.left.layer = p.layer + 1;
q.offer(p.left);
}
if(p.right != null){
p.right.layer = p.layer + 1;
q.offer(p.right);
}
}
}
@Test
public void test(){
int[] a = {
1,2,4,5,3,6,7};
int[] b = {
4,2,5,1,6,3,7};
Node root = create(a, b);
preOrder(root);
System.out.println();
inOrder(root);
System.out.println();
layerOrder(root);
}
}
普通树的定义
class Node{
int layer;//层号
int data;
List<Node> children;
}
二叉查找树BST
BST 又称排序二叉树,二叉搜索树。
定义:1,要么二叉查找树是一颗空树。
2,要么二叉树由左右子树组成,其中左子树和右子树都是二叉查找树,且左子树上所有节点的数据域均小于或等于根节点的数据域,右子树上的所有节点的数据域均大于根节点的数据域。
平衡二叉树
并查集
并查集是一种维护集合的数据结构,并查集支持下面两个操作:
1,合并:合并2个集合。2,查找:判断两个元素是否在一个集合。
并查集使用一个数组来实现:int father[n];其中,father[i]表示元素i的父亲节点,如果father[i] = [i]则说明元素i是该集合的根节点。
package perday;
import org.junit.Test;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class MyTest {
int n = 10;
int[] father = new int[10];
/**
* 初始化,一开始每个元素都是一个独立的集合,因此需要所有的father[i]=i
*/
void init(){
for (int i = 0; i < n; i++) {
father[i] = i;
}
}
/**
* 返回元素x所在集合的根节点(使用路径压缩)
* @param x
* @return
*/
int findFather(int x){
int a = x;
while (x != father[x]){
x = father[x];
}
// 此时x = father[x] x即为传来参数a的根节点
while (a != father[a]){
int z = a;
a = father[a];//a指向下一个节点
father[z] = x;//原来a的父亲节点指向x,也就是跟根节点
}
return x;
}
/**
* 把a,和b所在的集合合并起来
* @param a
* @param b
*/
void union(int a, int b){
int faA = findFather(a);
int faB = findFather(b);
if(faA != faB){
father[faA] = faB;
}
}
}
朋友圈 LeetCode547
https://leetcode-cn.com/problems/friend-circles/
班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。
给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。如果M[i][j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
示例 1:
输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出:2
解释:已知学生 0 和学生 1 互为朋友,他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回 2 。
class Solution {
//使用并查集
int[] father = new int[201];
void init(int n){
for (int i = 0; i < n; i++) {
father[i] = i;
}
}
int findFather(int x){
int a = x;
while (x != father[x]){
x = father[x];
}
//路径压缩
while (a != father[a]){
int z = a;
a = father[a];
father[z] = x;
}
return x;
}
void union(int a, int b){
int faA = findFather(a);
int fab = findFather(b);
if (faA != fab){
father[faA] = fab;
}
}
public int findCircleNum(int[][] M) {
int n = M.length;
init(n);
for (int i = 0; i < n; i ++){
//只用遍历一半就行了
for (int j = i + 1; j < n; j ++){
if(M[i][j] == 1){
//说明i和j是朋友
union(i, j);
}
}
}
int ans = 0;
for (int i = 0; i < n; i++) {
if(i == father[i]){
ans ++;
}
}
return ans;
}
}
堆
堆是一棵完全二叉树,树种的每个结点的值都不小于其左右孩子结点的值,那么称这样的堆为大顶堆。大顶堆堆一般用于优先队列的实现。
堆使用数组来表示,heap[1]代表堆顶元素。
创建堆
1,建立堆,
建立堆的过程总是从右到左从上到下 依此调整有孩子的节点成为最最大/小堆,时间复杂度O(n)
//1,建立大顶堆,
//建立堆的过程总是从右到左从上到下 依此调整有孩子的节点成为最最大/小堆
void createHeap(int[] a) {
n = a.length;
for (int i = 1; i <= a.length; i++) {
heap[i] = a[i - 1];
}
for (int i = n / 2; i >= 1; i --){
downAdjust(i, n);
}
}
//向下调整,范围[low,high]
//low为预调整节点的数组下标,high一般为堆的左后一个元素的数组下标
void downAdjust(int low, int high) {
int i = low, j = i * 2;
while (j <= high) {
//使j指向较大的孩子节点
if (j + 1 <= high && heap[j + 1] > heap[j]) {
j = j + 1;
}
//如果孩子的权值比要i大,则可以调整,否则调结束
if (heap[j] > heap[i]) {
int temp = heap[j];
heap[j] = heap[i];
heap[i] = temp;
i = j;
j = 2 * i;
} else {
break;
}
}
}
删除堆顶元素
如果删除堆中的最大元素,并让其保持堆的结构,只需要让最后一个元素覆盖堆顶元素,然后只需要调整堆顶元素即可(因为此时除了堆顶元素,其他节点都已经是最大堆)。时间复杂度O(logn)
//删除堆顶元素
int deleteTop() {
int top = heap[1];
heap[1] = heap[n--];
downAdjust(1, n);
return top;
}
添加一个元素
如果要添加一个元素,可以把元素放到数组的最后面,然后不断的向上调整这个元素即可。
//插入一个节点
void insert(int x){
heap[++n] = x;
upAdjust(1, n);
}
//对heap数组在[low,high]范围进行向上调整
//其中low一般设置为1,high表示欲调整的数组下标
void upAdjust(int low, int high){
int i = high, j = i / 2;//j 是i 的父亲节点
while (j >= low){
//如果孩子的权值较大,则需要调整
if(heap[i] > heap[j]){
int temp = heap[j];
heap[j] = heap[i];
heap[i] = temp;
i = j;
j = i / 2;
}else {
break;
}
}
}
堆排序
- 建立最大堆可以进行升序排序
- 最小堆可以降序排序
对于一个最大堆来说,取出堆顶元素,然后将堆的最后一个元素替换至堆顶。在进行一次针对堆顶元素的向下调整。
void heapSort(int[] a) {
createHeap(a);
for (int i = n; i >= 1; i--) {
int temp = heap[i];
heap[i] = heap[1];
heap[1] = temp;
downAdjust(1, i - 1);
}
}
完整代码
package perday;
import org.junit.Test;
/**
* @author TylerChen
* @date 2020/12/15 - 9:54
*/
public class Heap {
int maxn = 100;
int[] heap = new int[maxn];
int n;//堆种元素的个数
//1,建立大顶堆,
//建立堆的过程总是从右到左从上到下 依此调整有孩子的节点成为最最大/小堆
void createHeap(int[] a) {
n = a.length;
for (int i = 1; i <= a.length; i++) {
heap[i] = a[i - 1];
}
for (int i = n / 2; i >= 1; i--) {
downAdjust(i, n);
}
}
//删除堆顶元素
int deleteTop() {
int top = heap[1];
heap[1] = heap[n--];
downAdjust(1, n);
return top;
}
//插入一个节点
void insert(int x) {
heap[++n] = x;
upAdjust(1, n);
}
void heapSort(int[] a) {
createHeap(a);
for (int i = n; i >= 1; i--) {
int temp = heap[i];
heap[i] = heap[1];
heap[1] = temp;
downAdjust(1, i - 1);
}
}
void print(){
for (int i = 1; i <= n ; i++) {
System.out.print(heap[i] + " ");
}
}
@Test
public void test(){
int[] a = {
9,3,5,2,6,1,8,4,7};
createHeap(a);
print();//9 7 8 4 6 1 5 3 2
System.out.println();
deleteTop();
print();// 8 7 5 4 6 1 2 3
System.out.println();
insert(7);
print();// 8 7 5 7 6 1 2 3 4
System.out.println();
heapSort(a);
print();//1 2 3 4 5 6 7 8 9
}
//向下调整,范围[low,high]
//low为预调整节点的数组下标,high一般为堆的左后一个元素的数组下标
void downAdjust(int low, int high) {
int i = low, j = i * 2;
while (j <= high) {
//使j指向较大的孩子节点
if (j + 1 <= high && heap[j + 1] > heap[j]) {
j = j + 1;
}
//如果孩子的权值比要i大,则可以调整,否则调结束
if (heap[j] > heap[i]) {
int temp = heap[j];
heap[j] = heap[i];
heap[i] = temp;
i = j;
j = 2 * i;
} else {
break;
}
}
}
//对heap数组在[low,high]范围进行向上调整
//其中low一般设置为1,high表示欲调整的数组下标
void upAdjust(int low, int high) {
int i = high, j = i / 2;//j 是i 的父亲节点
while (j >= low) {
//如果孩子的权值较大,则需要调整
if (heap[i] > heap[j]) {
int temp = heap[j];
heap[j] = heap[i];
heap[i] = temp;
i = j;
j = i / 2;
} else {
break;
}
}
}
}
图
Dijkstra算法 (算法笔记367)
Dijkstra算法解决单源最短路径问题,即给定图G(V,E),和起点s,求从起点s到达其他顶点的最短距离
算法策略:
设置集合S存放已访问的顶点,然后执行n次下面2个步骤:
- 每次从集合V-S(为被访问的顶点集合)中选择与起点s的最短距离最小的一个顶点(记为u),访问并加入集合S。
- 之后,令顶点u为中介点,优化起点与所有从u能到达的顶点v之间的最短距离。
关键点:
- 集合S可以用一个bool型的数组vis[] 来实现,即当vis[i] == true的时候,表示顶点Vi 已被访问,反之则未被访问。
- 令int型数组d[] 表示起点s到达顶点Vi 的最短距离,初始时除了起点d[s]赋值为0,其余顶点都赋值为一个很大的数来表示inf(可以是100000000 10^9 也可以时 0x3fffffff (30位1),不要使用0x7fffffff 因为2个这样的数相加可能会超出整数范围)。
模板伪代码
初始化
for (循环n次){
u = 使d[u]最小的且还未被访问的顶点;
设置u被访问;
for(从u出发能到达的所有顶点v){
if(v没有被访问&&以u为中介使s到达顶点v的最短距离d[v]更优){
优化d[v]
}
}
}
实现:C++
使用邻接表实现
const int maxv = 510; //最大点的个数
const int INF = 0x3fffffff;
struct Node {
int v; //node的目标点
int d;// 到达目标点的距离
};
vector G[maxv]; //图
int d[maxv];//最短路径,
bool visited[maxv] = {false};
int N, C1, C2;//N,点的个数,C1,起点
void dijkstra() {
//使用dijkstra算法求最短路径
fill(d, d + maxv, INF);
d[C1] = 0;
for (int i = 0; i < N; ++i) {
int u = -1, min = INF;
//寻找从起点开始到达点的最小值
for (int j = 0; j < N; ++j) {
if (visited[j] == false && d[j] < min) {
u = j;
min = d[u];
}
}
if (u == -1) { //找不到对应点了
return;
}
visited[u] = true;//将这个点放到已访问集合中
for (int v = 0; v < G[u].size(); v++) {
Node node = G[u][v];
if (visited[node.v] == false) {
if (node.d + d[u] < d[node.v]) {
d[node.v] = node.d + d[u];
}
}
}
}
}
求最短路径
使d[v]变得更小得方案是让u作为作为s到顶点v路径最短路径上v得前一个节点,不妨把这个信息记录下来。设置一个数组pre[], 令pre[v]表示从起点s到顶点v得最短路径上v的前一个顶点(即前驱结点)的编号。
做法:
初始化
初始状态设置每一个点的前驱结点为自身
for(int i=0;i<n;i ++){
pre[i]=i;
}
....
if(v没有被访问&&以u为中介使s到达顶点v的最短距离d[v]更优){
优化d[v];
pre[v] = u
}
通过递归打印最短路径
//求s到v的最短路径
void DFS(int s, int v){
if(v == s){
printf("%d",s);
return;
}
DFS(s,pre[v]);
printf("->%d",v);
}
获得所有最短路径
使用一个线性表数组来记录所有最端路径
vector , 例如pre[v] = {1,2}表示从 起点s到达v 可以通过连个前驱到达,而且路径长度都是一样长的。(也可以使用treeset 这样对于查询某个顶点u是否再顶点v的前驱中的题目很方便 )
做法:
只需要在优化d[v]的时候做操作就可。
for(int v = 0; v < n; v ++){
if(vis[v] == false && G[u][v] != INF){
if(d[u] + G[u][v] < d[v]){//以u为中介点可以使得d[v]更优
d[v] = d[u] + G[u][v];
pre[v].clear();// 被清除的不是最短路径的前驱
pre[v].push_back(u);
}else if(d[u] + G[u][v] == d[v]){
pre[v].push_back(u);
}
}
}
获得所有最短路径:
//获取从s到达v的所有最短路径
vector< vector > allpath;
vector temp;
void getALLShortest(int s, int v){
if(v == s){ //到达了叶子结点st。即路径的起点
temp.push_back(v);
allpath.push_back(temp);
//将temp倒序输出即可得到正确的路径
for (int i = temp.size() - 1; i >= 0 ; --i) {
printf("%d ",temp[i]);
}
printf("\n");
temp.pop_back();
return;
}
temp.push_back(v);
for (int i = 0; i < pre1[v].size(); ++i) {
int a = pre1[v][i];
getALLShortest(s,a);
}
temp.pop_back();
}
其他标尺
对于以下三种情况,都只需要增加一个数组来存放新增的边权或点权或最短路径的条数。然后只需要修改优化d[v]那部分代码即可。
增加边权
给每条边在增加一个边权(例如花费),然后求在最短路径有多条的情况下要求路径上的花费之和最小
用cost[u][v]表示u->v的花费,增加一个数组c[],令从起点s到达顶点u的最小花费为c[u]。初始化的时候只有c[s]为0、其余c[u]均为INF。
for(int v = 0; v < n; v ++){
if(vis[v] == false && G[u][v] != INF){
if(d[u] + G[u][v] < d[v]){//以u为中介点可以使得d[v]更优
d[v] = d[u] + G[u][v];
c[v] = c[u] + cost[u][v];//因为此时最短路径要经过u,所以花费必须经过u到达v
}else if(d[u] + G[u][v] == d[v]){
if(c[u] + cost[u][v] < c[v]){//当前这个也是最短路径,看看经过当前u到达v的花费是否更小
c[v] = c[u] + cost[u][v];
}
}
}
}
增加点权
给每个点增加一个点权(例如每个城市可以收集到的物资),然后再最短路径有多条时要求路径上的点权之和最大。
用weight[u]表示点权(城市中物资的个数),求最短路径情况下的最大点权(物资)。增加一个数组w[],w[u]表示最短路径情况下从起点s到达点u的能收集到的最大物资数(最短路径下各个点权之和)。初始化的时候w[s] = weight[s]、其余w[u]均为0。
for(int v = 0; v < n; v ++){
if(vis[v] == false && G[u][v] != INF){
if(d[u] + G[u][v] < d[v]){//以u为中介点可以使得d[v]更优
d[v] = d[u] + G[u][v];
w[v] = w[u] + weight[v];//因为此时最短路径要经过u,所以收集到的物资必须从u到v
}else if(d[u] + G[u][v] == d[v]){
if(w[u] + weight[v] > w[v]){//当前这个也是最短路径,看看经过当前u到达v的物资是否更多
w[v] = w[u] + weight[v];
}
}
}
}
最短路径的条数
增加一个数组nums[],nums[u]表示从起点s出发到达u最短路径的条数。初始化时只有nums[s]=1,其余均为0
for(int v = 0; v < n; v ++){
if(vis[v] == false && G[u][v] != INF){
if(d[u] + G[u][v] < d[v]){//以u为中介点可以使得d[v]更优
d[v] = d[u] + G[u][v];
nums[v] = nums[u]; //等于能到达u的所有最短路径个数
}else if(d[u] + G[u][v] == d[v]){
nums[v] += nums[u]; //加上能到达u的所有最短路径个数
}
}
}
使用DFS获得其他标尺 Dijkstra + DFS
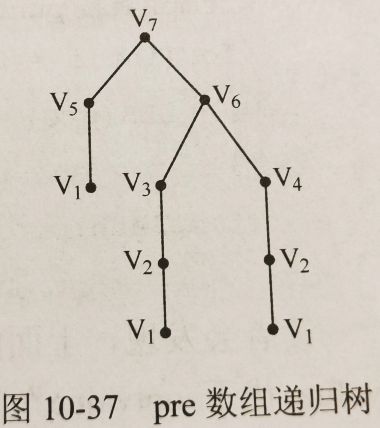
参看获得所有最端路径,可得递归树:
对这样一棵进行遍历的时候,每次到达叶子结点(起点),就会产生一条完整的路径。因此每次得到这样一条路径,就可以对这条路径计算其第二标尺(例如把路径上的边权或者是点权累加出来),令其与当前第二标尺的最优值进行比较。如果比当前最优值更优,则更新最优值,并用这条路径覆盖最优路径。这样当所有最短路径都遍历完毕后,就可以得到最短路径下的最优标尺了。
这样依赖,可以先通过dijkstra获得最短路径,以及其前驱pre,然后通过DFS即可求得题目所需要的标尺啦!
const int maxv = 510; //最大点的个数
const int INF = 0x3fffffff;
struct Node {
int v; //node的目标点
int d;// 到达目标点的距离
};
vector G[maxv]; //图
int d[maxv];//最短路径,
bool visited[maxv] = {false};
int N, C1, C2;//N,点的个数,C1,起点
void dijkstra() {
//使用dijkstra算法求最短路径
fill(d, d + maxv, INF);
d[C1] = 0;
for (int i = 0; i < N; ++i) {
int u = -1, min = INF;
//寻找从起点开始到达点的最小值
for (int j = 0; j < N; ++j) {
if (visited[j] == false && d[j] < min) {
u = j;
min = d[u];
}
}
if (u == -1) { //找不到对应点了
return;
}
visited[u] = true;//将这个点放到已访问集合中
for (int v = 0; v < G[u].size(); v++) {
Node node = G[u][v];
if (visited[node.v] == false) {
if (node.d + d[u] < d[node.v]) {
d[node.v] = node.d + d[u];
pre[v].clear();
pre[v].push_back(u);
}else if(node.d + d[u] == d[node.v]){
pre[v].push_back(u);
}
}
}
}
}
使用DFS 解题!伪代码如下:
int optvalue; //第二标尺的最优值
vector pre[maxv];//存放结点的前驱结点
vector temp,path; //临时路径、最优路径
void getALLShortest(int s, int v){ //v为当前访问的点
if(v == s){ //到达了叶子结点s。即路径的起点
temp.push_back(v);
int value;
计算路径temp上面的value值;
if(value优于optValue){
optValue=value;
path = temp;
}
temp.pop_back();
return;
}
temp.push_back(v);
for (int i = 0; i < pre1[v].size(); ++i) {
int a = pre[v][i];
getALLShortest(s,a);
}
temp.pop_back();
}
注意:通过这种做法也可以求最短路径的个数,可以开一个全局变量,每当到达叶子结点的时候令这个全局变量加1即可。
例题
题目详情 (pintia.cn)
1003 Emergency (25分)
As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input Specification:
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (≤500) - the number of cities (and the cities are numbered from 0 to N−1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1, c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output Specification:
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input:
5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1
Sample Output:
2 4
解答1 一次Dijkstra
#include
#include
#include
#include
using namespace std;
const int maxv = 510; //最大点的个数
const int INF = 0x3fffffff;
struct Node {
int v; //node的目标点
int d;// 到达目标点的距离
};
vector G[maxv]; //图
int weight[maxv]; //点权,每个地方可以用的人手
int d[maxv];//最短路径,
int nums[maxv];//到达某个点的路径个数
int c[maxv];//到达某个点可用人手的最多数量
bool visited[maxv] = {false};
int N, M, C1, C2;//城市的个数,路的个数,C1,起点,C2,终点
void dijkstra() {
//使用dijkstra算法求最短路径
fill(d, d + maxv, INF);
c[C1] = weight[C1]; //
d[C1] = 0;
nums[C1] = 1;//到达起点的路径个数设为1
for (int i = 0; i < N; ++i) {
int u = -1, min = INF;
//寻找从起点开始到达点的最小值
for (int j = 0; j < N; ++j) {
if (visited[j] == false && d[j] < min) {
u = j;
min = d[u];
}
}
if (u == -1) { //找不到对应点了
return;
}
visited[u] = true;//将这个点放到已访问集合中
for (int v = 0; v < G[u].size(); v++) {
Node node = G[u][v];
if (visited[node.v] == false) {
if (node.d + d[u] < d[node.v]) {
c[node.v] = c[u] + weight[node.v];
d[node.v] = node.d + d[u];
nums[node.v] = nums[u];
}else if(d[u] + node.d == d[node.v]){
if(c[u] + weight[node.v] > c[node.v]){
c[node.v] = c[u] + weight[node.v];
}
nums[node.v] += nums[u];
}
}
}
}
}
int main() {
scanf("%d%d%d%d", &N, &M, &C1, &C2);
for (int i = 0; i < N; ++i) {
scanf("%d", weight + i);
}
int a, b, w;
for (int i = 0; i < M; ++i) {
scanf("%d%d%d", &a, &b, &w);
Node n;
n.v = b;
n.d = w;
G[a].push_back(n);
}
dijkstra();
printf("%d %d",nums[C2], c[C2]);
return 0;
}
解答2 Dijkstra + DFS
#include
#include
#include
#include
using namespace std;
const int maxn = 510;//最大的结点个数
const int INF = 0x3fffffff;
int N, M, C1, C2;//城市的个数,路径的个数,当前所在的城市(起点),需要救援的城市(终点)
struct Node {
int target; //目的城市
int dis; //到达目的城市的距离
};
vector G[maxn]; //邻接表
vector pre[maxn]; //存放前驱结点
int weight[maxn]; //存放每个城市的人手个数,(点权)
int d[maxn];//到达某个顶点的最短路径
bool vis[maxn] = {false};//判断某个顶点是否被访问过了
void dijkstra(){
fill(d, d + maxn, INF);
d[C1] = 0;
for (int i = 0; i < N; ++i) {
int u = -1, min = INF;
for (int j = 0; j < N; ++j) {
if(vis[j] == false && d[j] < min){
min = d[j];
u = j;
}
}
if(u == -1){
return;
}
vis[u] = true;
for(int k = 0;k < G[u].size(); k ++){
Node next = G[u][k];
if(vis[next.target] == false){
if(next.dis + d[u] < d[next.target]){
d[next.target] = next.dis + d[u];
pre[next.target].clear();
pre[next.target].push_back(u);
}else if(next.dis + d[u] == d[next.target]){
pre[next.target].push_back(u);
}
}
}
}
}
int maxNums = -1;//最短路径下的最多人手初始设置为-1
int nums = 0;//最短路径的个数
vector temp;//保存这临时最短路径
void DFS(int s, int v){
if(s == v){
nums ++;
temp.push_back(s);
int value = 0;
for (int i = 0; i < temp.size(); ++i) {
value += weight[temp[i]];
}
maxNums = max(maxNums, value);
temp.pop_back();
return;
}
temp.push_back(v);
for (int i = 0; i < pre[v].size(); ++i) {
DFS(s, pre[v][i]);
}
temp.pop_back();
}
int main() {
scanf("%d%d%d%d", &N, &M, &C1, &C2);
for (int i = 0; i < N; ++i) {
scanf("%d", i + weight);
}
int a, b, c;
for (int i = 0; i < M; ++i) {
scanf("%d%d%d", &a, &b, &c);
Node node;
node.target = b;
node.dis = c;
G[a].push_back(node);
}
dijkstra();
DFS(C1, C2);
printf("%d %d", nums, maxNums);
}
1030 Travel Plan(30分)
https://pintia.cn/problem-sets/994805342720868352/problems/994805464397627392
旅行者得地图上面有2个城市之间的距离和花费,给定起点和终点,求他们之间最小路径,可能不止一条,求其中花费最小一条。
输入规格:
第一行4个数:N,M,S,D。分别为城市个数 <= 500, M 公路条数<= 500 ,(城市的编号是0-N-1),起点,终点。
后面是M行:
City1 City2 Distance Cost
sample input
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出规格:
输出从起点到终点的最优路径,最优路径的长度,和花费
sample output
0 2 3 3 40
解答:Dijkstra + DFS
#include
#include
#include
using namespace std;
const int maxv = 510; //最大点的个数
const int INF = 0x3fffffff;
int d[maxv];//最短路径
bool vis[maxv];
int N, M, S, D;//城市的个数,高速公路的个数,起点,目的地址
int G[maxv][maxv];
int cost[maxv][maxv];
vector pre[maxv];//前驱结点
void dijkstra() {
fill(d, d + maxv, INF);
d[S] = 0;
for (int i = 0; i < N; ++i) {
int u = -1, min = INF;
for (int j = 0; j < N; ++j) {
if (vis[j] == false && d[j] < min) {
u = j;
min = d[j];
}
}
if (u == -1) {
return;
}
vis[u] = true;
for (int j = 0; j < N; ++j) {
//如果u->j可达 && j没有被访问过
if (G[u][j] != INF && vis[j] == false) {
if (d[u] + G[u][j] < d[j]) {
d[j] = d[u] + G[u][j];
pre[j].clear();
pre[j].push_back(u);
} else if (d[u] + G[u][j] == d[j]) {
pre[j].push_back(u);
}
}
}
}
}
vector path, temp;//最优路径,临时路径
int minCost = INF;
void DFS(int s, int v) {
if (s == v) {
temp.push_back(s);
int value = 0;
for (int i = temp.size() - 1; i > 0; --i) {
value += cost[temp[i]][temp[i - 1]];
}
if (value < minCost) {
minCost = value;
path = temp;
}
temp.pop_back();
return;
}
temp.push_back(v);
for (int i = 0; i < pre[v].size(); ++i) {
DFS(s, pre[v][i]);
}
temp.pop_back();
}
int main() {
fill(G[0], G[0] + maxv * maxv, INF);
scanf("%d%d%d%d", &N, &M, &S, &D);
int a, b, c, d1;
for (int i = 0; i < M; ++i) {
scanf("%d%d%d%d", &a, &b, &c, &d1);
G[a][b] = c;
G[b][a] = c;
cost[a][b] = d1;
cost[b][a] = d1;
}
dijkstra();
DFS(S, D);
for (int i = path.size() - 1; i >= 0; --i) {
printf("%d ", path[i]);
}
printf("%d %d", d[D], minCost);
return 0;
}
Bellman-Ford算法和SPFA算法
Bellman-Ford 算法
概述
Dijkstra算法可以很好的解决无负权图的最短路径问题,但是如果出现了负权边,Dijkstra算法就会失效。
Bellman-Ford算法也可以解决单源最短路径的问题,但是可以处理有负权边的情况。
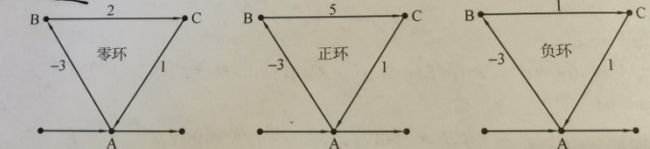
根据环中边的边权之和的正负,可以将环分为零环、正环和负环。
显然:零环和正环不会影响最短路径的求解,因为0环的存在不能使得最短路径变得更短。如果负环无法从源点出发到达,则最短路径的求解不会收到影响。
BF算法返回一个bool值,如果存在从源点可达的负环,那么函数将返回false;否则将返回true,此时数组d中存放的就是从源点到达各顶点的最短距离。
算法思想
对图中的边进行V-1轮操作,每轮都遍历图中的所有边:对每条边u->v,如果u为中介点可以使d[v]更小,即d[u] + length[u->v] < d[v],则用d[u] + length[u->v] 更新d[v]。时间复杂度O(VE);
伪代码:
for(int i = 0; i < n - 1; i ++){
for(each edge u->v){
if(d[u] + length[u->v] < d[v]){
d[v] = d[u] + length[u->v]
}
}
}
此时如果途中没有从源点可达的负环,那么数组d中的所有值都应该使最优。因此需要对所有边在进行一轮操作,判断是否有某条边u->v仍然满足d[u] + length[u->v] < d[v]。如果有,则说明图中有从源点可达的负环,返回false。否则说明数组d中的所有值都已经达到最优。
for(each edge u->v){
if(d[u] + length[u->v] < d[v]){
return false;
}
}
return true;
证明算法的正确性
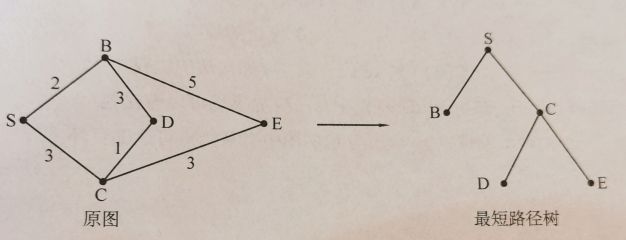
首先,如果最短路径存在,则最短路径上顶点的个数不会超过V个,否则肯定有环。于是把源点作为根节点可以得到一棵最短路径树。
初始情况下d[s] = 0 第一层被确定了;然后遍历一次所有边,可以确定第二层的最短路径,d[B]=2,d[C] =3,其他层不确定是最小的;接着遍历则可以确定第三层的,直到确定所有层的最短路径。
实现:使用邻接表
使用邻接矩阵会使时间复杂度上升到O(V^3);这里有一个小技巧:如果在某一轮操作后没发现没有边被松弛,说明数组d中的所有值都已经达到了最优,提前退出即可。
const int maxv = 510; //最大点的个数
const int INF = 0x3fffffff;
struct Node {
int v,dis;
};
vector G[maxv];
int n;
int d[maxv];
bool Bellman_Ford(int s){
fill(d, maxv + d, INF);
d[s] = 0;
for (int i = 0; i < n - 1; ++i) {
bool flag = true;
for (int u = 0; u < n; ++u) {
for (int j = 0; j < G[u].size(); ++j) {
int v = G[u][v].v;
int dis = G[u][v].dis;
if(d[u] + dis < d[v]){
d[v] = d[u] + dis;
flag = false;
}
}
}
if(flag){
return true;
}
}
//一下为判断负环的代码
for (int u = 0; u < n; ++u) {
for (int j = 0; j < G[u].size(); ++j) {
int v = G[u][v].v;
int dis = G[u][v].dis;
if(d[u] + dis < d[v]){
return false;
}
}
}
return true;
}
注意:统计最短路径条数的做法和Dijkstra不一样:因为BF算法期间会多次访问曾经访问过的顶点,如果单纯按照Dijkstra算法中介绍的num数组的写法,将会反复计算访问过的顶点。必须设置一个set数组,当遇到一条长度相同的路径时,必须重新计算已有最短路径的条数。(也可以还是按照DFS那种方法获得个数的)
const int maxv = 510; //最大点的个数
const int INF = 0x3fffffff;
struct Node {
int v,dis;
};
vector G[maxv];
int n;
int d[maxv];
int nums[maxv];
set pre[maxv];
bool Bellman_Ford(int s){
fill(d, maxv + d, INF);
d[s] = 0;
nums[maxv] = 1;
for (int i = 0; i < n - 1; ++i) {
bool flag = true;
for (int u = 0; u < n; ++u) {
for (int j = 0; j < G[u].size(); ++j) {
int v = G[u][v].v;
int dis = G[u][v].dis;
if(d[u] + dis < d[v]){
d[v] = d[u] + dis;
flag = false;
nums[v] = nums[u]
pre[v].clear():
pre[v].insert(u);
}else if(d[u] + dis == d[v]){
pre[v].insert(u);
nums[v]=0;
for(auto it = pre[v].begin(); it != pre[v].end(); it ++){
nums[v] += nums[*it];
}
}
}
}
if(flag){
return true;
}
}
//一下为判断负环的代码
for (int u = 0; u < n; ++u) {
for (int j = 0; j < G[u].size(); ++j) {
int v = G[u][v].v;
int dis = G[u][v].dis;
if(d[u] + dis < d[v]){
return false;
}
}
}
return true;
}
SPFA(Shortest Path Faster Algorithm)
Bellman-Ford算法很简洁,但是O(VE)的时间复杂度很高,注意到:只有当某个顶点u的d[u]值改变的时候,从它出发的边的邻接点v的d[v] 值才有可能被改变。
优化:建立一个队列(初始把源点加进去),每次将队首元素u取出,然后对u出发的所有边进行松弛操作,如果d[u] + len[u->v] < d[v],用d[u] + len[u->v] 覆盖d[v],于是d[v] 可以获得更优的值,如果v不在队列中,就把v加入到队列中。直到队列为空(说明图中没有从源点可达的负环),或者是某个顶点入队的次数超过v-1(说明存在负环)。
伪代码:
queue q;
q.push(s);
while(队列非空){
取出队首元素u;
for(所有的u->v){
if(d[u] + len[u->v] < d[v]){
d[v] = d[u] + len[u->v]
if(v不在队列){
v入队;
if(v入队的次数大于n-1){
说明有负环;
return;
}
}
}
}
}
优化后的算法叫做SPFA,期望时间复杂度为:O(KE)。如果有源点可达的负环,时间复杂度就会退成O(VE)。
代码:
const int maxv = 510; //最大点的个数
const int INF = 0x3fffffff;
struct Node {
int v,dis;
};
vector G[maxv];
int n;
int d[maxv];
bool inq[maxv] = {false};//判断顶点是否在队列中
int num[maxv];
bool SPFA(int s){
memset(num, 0, sizeof(num));
fill(d,d + maxv, INF);
queue q;
q.push(s);
inq[s] = true;
num[s] ++;
d[s] = 0;
while (!q.empty()){
int u = q.front();
q.pop();
inq[u] = false; //u 出队列,所以u不在队列中了
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i].v;
int dis = G[u][i].dis;
if(d[u] + dis < d[v]){
if(!inq[v]){
q.push(v);
inq[v] = true;
num[v] ++;
if(v >= n){
return false;
}
}
}
}
}
return true;//无可达环
}
注意:使用SPFA 也可以判断是否存在负环,如果负环从源点不可达,则需要添加一个辅助点C,并添加一条从源点到达C的有向边以及V-1条从C到达除源点以外各顶点的有向边才能判断负环是否存在。
Floyd算法
Floyd算法解决全员最短路径问题,时间复杂度是O(n^3)。
Floyd算法:如果存在顶点k,使得以k作为中介点i和j的当前最短距离缩短,则使用顶点k作为顶点i和j的中介点。即dis[i][k] + dis[k][j] < dis[i][j],则令 dis[i][j] = dis[i][k] + dis[k][j]
Floyd算法伪代码:
枚举顶点k
以顶点k作为中介点,枚举所有顶点对i,j
如果 dis[i][k] + dis[k][j] < dis[i][j]
则dis[i][j] = dis[i][k] + dis[k][j]
实现
const int INF = 0x3fffffff;
const int maxv = 200;
int n, m; //顶点数,边数
int dis[maxv][maxv];
int G[maxv][maxv];
void Floyd(){
//初始化
//将图中的数据赋值给dis,图中不存在的边为INF,dis中需要修改下
for (int i = 0; i < n; ++i) {
dis[i][i] = 0;
}
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if(dis[i][k] != INF && dis[k][j] != INF && dis[i][k] + dis[k][j] < dis[i][j]){
dis[i][j] = dis[i][k] + dis[k][j];
}
}
}
}
}
最小生成树算法
最小生成树(MST Minimum Spanning Tree):给定一个无向图G(V,E),求一棵树T使得这棵树包含G的所有顶点,所有边都来自G,并且满足整棵树的边权最小。
Prim算法
基本思想
对图G(V,E) 设置集合S,存放已被访问的顶点, V-S表示未被访问的点。每次从集合V-S中选择与集合S的最短距离最小的一个顶点u,访问并加入集合。之后以u为中介点,优化所有能从u到达的顶点v与集合S之间的最短距离。
和Dijkstra算法很像。只有优化的部分不一样。
直接上代码
邻接表实现
const int maxv = 510; //最大点的个数
const int INF = 0x3fffffff;
struct Node {
int v; //node的目标点
int d;// 到达目标点的距离
};
vector G[maxv]; //图
int d[maxv];//距离集合S的最短路径,
bool visited[maxv] = {false};
int N, C1;//N,点的个数,C1,起点
int ans = 0; //存放最小生成树的边权集合
void prim() {
//使用dijkstra算法求最短路径
fill(d, d + maxv, INF);
d[C1] = 0;
for (int i = 0; i < N; ++i) {
int u = -1, min = INF;
//寻找从起点开始到达点的最小值
for (int j = 0; j < N; ++j) {
if (visited[j] == false && d[j] < min) {
u = j;
min = d[u];
}
}
if (u == -1) { //找不到对应点了
return;
}
visited[u] = true;//将这个点放到已访问集合中
ans += d[u];
for (int v = 0; v < G[u].size(); v++) {
Node node = G[u][v];
if (visited[node.v] == false) {
if (node.d < d[node.v]) {//如果u->v的距离,小于d[v],则更新
d[node.v] = node.d;
}
}
}
}
}
注意
prim算法时间复杂度为O(V^2),使用邻接表通过堆优化时间复杂度降为O(VlogV + E) 。说明,尽量在图的顶点较少而边较多的情况下使用prim算法。
Kruskal算法
基本思想:
克鲁斯卡尔算法使用边贪心算法,基本思想为:
初始情况下,擦掉所有的边。然后执行下面步骤:
- 对所有边按边权从小到达进行排序。
- 按照边权从小到达测试所有边,如果当前测试边所连接的顶点不在一个连同块中,则把这条边加入当前的最小生成树中。
- 执行步骤2直到最小生成树的边等于V-1
伪代码
void kruskal(){
令最小生成树的边权和ans=0,最小生成树当前边数num=0;
将所有边排序;
for(从小到达枚举边e){
if(e的两个顶点不在一个联通块中){
ans = e.cost;
num ++;
if(num == v-1){
return;
}
}
}
}
如何判断两个顶点是否在一个集合中? 并查集
实现
#include
#include
#include
using namespace std;
const int maxv = 500;
struct Edge {
int u, v;
int cost;
}edge[maxv];
//边权从小到达排序
bool cmp(Edge a, Edge b){
return a.cost < b.cost;
}
int n;//顶点个数
int father[maxv];
void init(){
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
int findFather(int x){
int a = x;
while (x != father[x]){
x = father[x];
}
while (a != father[a]){
int z = a;
a = father[a];
father[z] = x;
}
return x;
}
int kruskal(int m){//m为边的个数
int ans = 0,num_edge = 0;
init();//并查集初始化
sort(edge,edge + m, cmp);
for (int i = 0; i < m; ++i) {
int faU = findFather(edge[i].u);
int faV = findFather(edge[i].v);
if(faU != faV){ //如果不在一个集合中
father[faU] = faV;//合并集合
ans += edge[i].cost;
num_edge ++;
if(num_edge == n -1){//边已经够了,
break;
}
}
}
return ans;
}
拓扑排序
拓扑排序的很重要的一个应用是判断一个给定的图是否是有向无环图。
DAG(Directed Acyclic Graph, DAG): 有向无环图。
拓扑排序是将有向无环图G的所有顶点排成一个线性序列,使得对图G中的任意两个顶点u、v,如果存在u->v , 那么在序列中u一定在v的前面。
排序后(不唯一)
拓扑排序步骤:
- 定义一个队列Q,并把所有入度为0的结点加入队列。
- 取队首结点,输出。然后删除所有从他出发的边,并令这些边到达的顶点入度减一,如果某个顶点入度减为0,则将其加入队列。
- 反复进行2操作,直到队列为空。如果队列为空时入过队的结点数目恰好为n,说明拓扑排序成功,图G为有向无环图;否则拓扑排序失败,图G中有环。
实现:
#include
#include
#include
#include
#include
using namespace std;
const int maxv = 1000;
vector G[maxv];
int n, inDegree[maxv];//结点个数,某个结点的入度(在读入结点的时候可以确定)
bool topologicalSort(){
int num = 0; //加入拓扑序列的顶点个数
queue q;
for (int i = 0; i < n; ++i) {
if(inDegree[i] == 0){
q.push(i);//将所有入度为0的顶点加入队列
}
}
while (!q.empty()){
int u = q.front();
q.pop();
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i];//u的后继结点
inDegree[v] --;
if(inDegree[v] == 0){
q.push(v);
}
}
G[u].clear(); //清空顶点u的所有出边(入无必要可以不写)
num ++; //加入拓扑序列的顶点数加一
}
if(num == n){
return true; //拓扑排序成功,给定的图是有向无环图
}else{
return false; //说明图中有环
}
}
关键路径
AOV 网和 AOE网
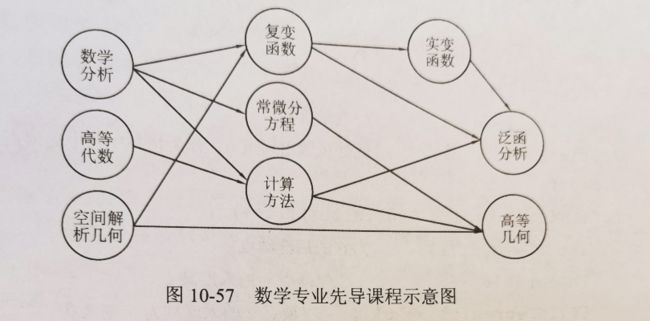
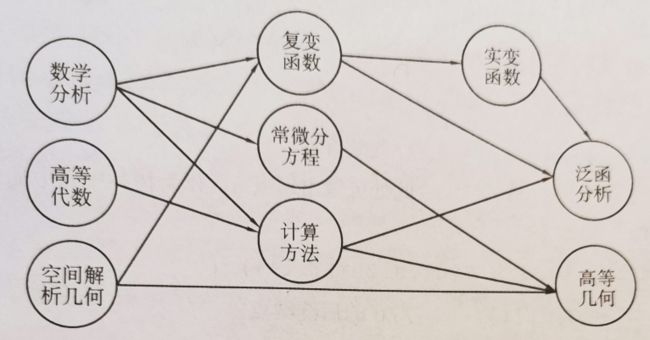
AOV网(Avtivity On Vertex)顶点活动图是指用顶点表示活动,而用边集表示活动间优先关系的有向图。如下图
AOE网(Avtivity On Vertex)边活动网是指用带权的边集表示活动,而用顶点表示事件的有向图,其中边权表示完成活动所需要的时间。如下图
考虑到工程总会有一个起始时刻和结束时刻,因此AOV网一般只有一个源点与结束点。
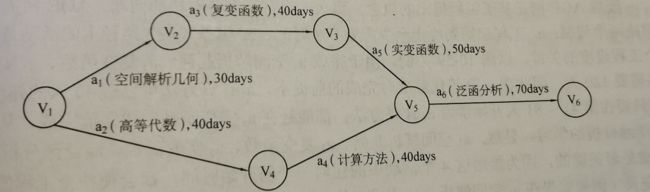
AOE网中的最长路径被称为关键路径,如a1 a3 a5 a6 就是关键路径,因为这条路径决定了工程的最短完成时间。
求最长路径
对一个没有正环的图,要求其最长路径,可以将所有的边权乘以-1,令其变为相反数,然后使用Bellman-Ford算法,或SPFA算法求最短路径,最后将结果求反即可。 注意:不能使用Dijkstra算法。
关键路径的求法 **
比较复杂,算法笔记p419
求解有向无环图的(DAG)最长路径的方法。
设置两个数组e,l 其中e[r] 和 l[r]分别表示活动ar 最早开始时间和最迟结束时间。求出数组后如果e[r] == l[r] ,表示活动r的最早开始时间和结束时间一样,证明 活动r是关键路径。
如何求解e, l ?
如图,事件Vi在经过活动ar到达事件Vj 。设置数组ve,vl, ve[i],vl[i]表示事件i 最早和最迟的发生时间。
- 对于ar来说,e[r] = ve[i],活动r的最早发生时间,就是事件i的最早发生时间。
- l[r] + len[r] = vl[j] 活动r最迟发生事件,加上活动r所需要的时间,就是事件j的最迟发生时间。
于是求解出ve,和vl 就可以求出e 和 l
求解ve – 事件的最早发生时间
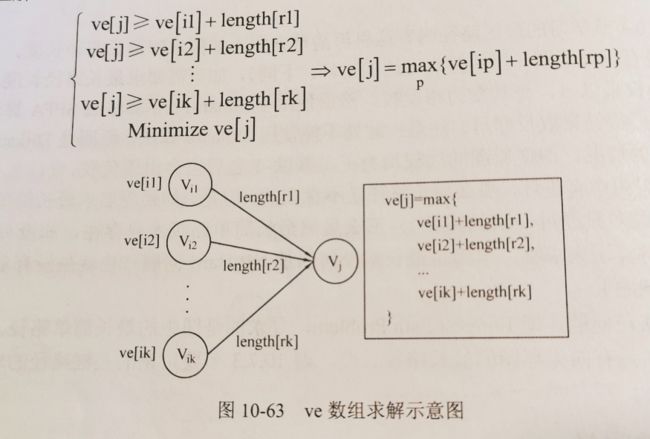
如图,Vj的最早发生时间就是ve[i1] + len[r1] ~ ve[ik] + len[rk]中的最大值。因为Vj的发生要等到所有Vi 都发生才能发生。
可以发现,要想获得ve[j]的正确值,ve[i1] ~ ve[ik]都必须已经得到了。因此,在访问vj时必须保证其前驱结点都已经被访问过,可以使用拓扑排序。一个好的做法时,在拓扑排序访问到vi时,让ve[i]更新ve[j]的值,这样访问到ve[j]时,ve[j]的所有前驱都已更新过它,保证了它的正确性。
#include
#include
#include
#include
using namespace std;
struct Node{
int v,w;
};
const int maxv = 100;
vector G[maxv];
//拓扑排序
int n;//顶点个数
int inDegree[maxv];
int ve[maxv], vl[maxv];
stack topOrder;
bool topologicalSort(){
queue q;
for (int i = 0; i < n; ++i) {
if(inDegree[i] == 0){
q.push(i);
}
}
while (!q.empty()){
int u = q.front();
q.pop();
topOrder.push(u);
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i].v;
inDegree[v] --;
if(inDegree[v] == 0){
q.push(v);
}
if(ve[u] + G[u][i].w > ve[v]){
ve[v] = ve[u] + G[u][i].w;
}
}
}
if(topOrder.size() == n){
return true;
}
return false;
}
求解vl–事件发生的最晚时间
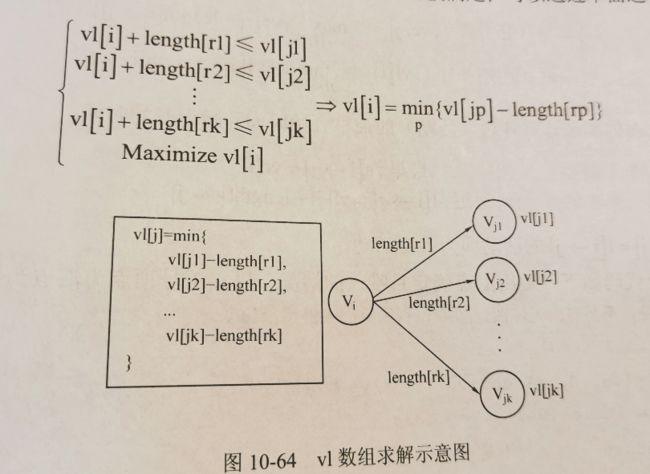
如图,vi 的最迟发生时间,就是vl[j1] - len[r1] ~ vl[jk] - len[rk]中的最小值,这样的话能保证所有vj都能在,规定时间内完成。
如何实现?可以使用拓扑逆序列来实现。
如图,当访问vj的时候,用vl[j]更新vl[i],这样当v[i] 被访问到的时候就一定是正确的。在拓扑逆序列中vj 一定在vi之前被访问。
void getVl(){
//初始值,都设置为终点的最迟(早)发生时间。
fill(vl, vl + n, ve[n -1 ]);
while(!topOrder.empty()){
int u = topOrder.top();
topOrder.pop();
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i].v;//
if(vl[u] - G[u][i].w < vl[u]){
vl[u] = vl[u] - G[u][i].w;
}
}
}
}
总结
最后的关键路径长度
如果事先不知道终点编号,那么关键路径的长度就是ve[]中最大的值。
完整代码
这里假设v[n-1]是 终点
#include
#include
#include
#include
#include
using namespace std;
struct Node{
int v,w;
};
const int maxv = 100;
vector G[maxv];
//拓扑排序
int n;//顶点个数
int inDegree[maxv];
int ve[maxv], vl[maxv];
stack topOrder;
bool topologicalSort(){
queue q;
for (int i = 0; i < n; ++i) {
if(inDegree[i] == 0){
q.push(i);
}
}
while (!q.empty()){
int u = q.front();
q.pop();
topOrder.push(u);
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i].v;
inDegree[v] --;
if(inDegree[v] == 0){
q.push(v);
}
if(ve[u] + G[u][i].w > ve[v]){
ve[v] = ve[u] + G[u][i].w;
}
}
}
if(topOrder.size() == n){
return true;
}
return false;
}
void getVl(){
//初始值,都设置为终点的最迟(早)发生时间。
fill(vl, vl + n, ve[n -1 ]);
while(!topOrder.empty()){
int u = topOrder.top();
topOrder.pop();
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i].v;//
if(vl[u] - G[u][i].w < vl[u]){
vl[u] = vl[u] - G[u][i].w;
}
}
}
}
int CriticalPath(){
memset(ve, 0, sizeof(ve));
if(topologicalSort() == false){
return -1;
}//有环
getVl();
//遍历所有边,计算活动的最早开始时间和e和最迟开始时间l
for (int u = 0; u < n; ++u) {
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i].v, w = G[u][i].w;
int e = ve[u], l = vl[v] - w;
if(e == l){
//输出关键路径
printf("%d->%d", u,v);
}
}
}
return ve[n - 1];//返回关键路径长度。
}
注意:可以使用动态规划求解关键路径
动态规划
如果一个问题的最优解可以由其子问题的最优解有效的构造出来,那么称这个问题的拥有最优子结构。一个问题必须拥有最优子结构和重叠子问题才能用动态规划去解决。
分治和动态规划的区别
分治和动态规划都是将问题分为子问题,然后合并子问题的解得到原问题的解。但是不同的是,分支法分解出来的子问题是不重叠的,因此**分治法解决的问题不拥有重叠子问题,而动态规划解决的问题拥有重叠子问题。**例如,归并排序和快速排序都是分别处理左序列和右序列,然后将左右序列的结果合并。分支法解决的不一定是最优化的问题,而动态规划解决的问题一定是最优化问题。
贪心与动态规划
贪心和动态规划都要求原问题必须拥有最优子结构。二者的区别在于,贪心法采用的类似于自顶向下,但是并不等待子问题求解完毕之后在选择使用哪个,而是通过一种策略直接选择一个子问题去求解。例如,对于数塔问题而言,贪心法从上层开始,每次选择左下和右下两个数字中的较大的一个,显然这不一定能得到最优解。而动态规划则会考虑所有子问题,并选择继承能得到最优结果的那个。
例题
斐波那契数列问题
令dp[i] 为 F(i)的 则dp[i] = dp[i-1] + dp[i - 2],边界条件为dp[0] = 1, dp[1] = 1
数塔问题
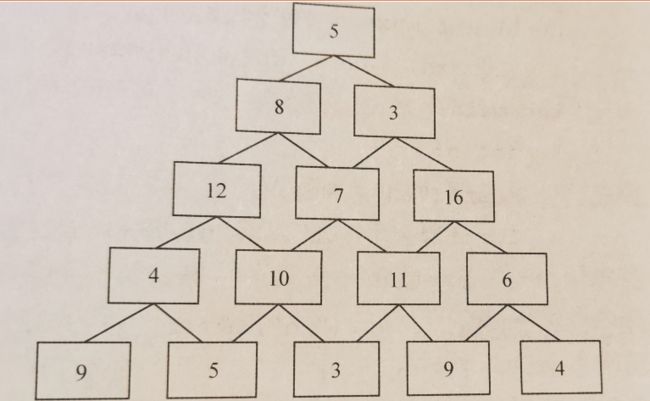
问题描述
从第一层走到第n层,每次只能走下一层连接的两个数字。问从最后路径上所有数字相加和最大是多少?
f[i][j]为第i行j列上的数字
求解
令
dp[i][j]表示从第i行第j个数字出发到达底层所有路径中能得到的最大和,则可得
dp[i][j] = max(dp[i+1][j],dp[i+1][j+1]) + f[i][j]边界条件为最后一层的值:
即
dp[n][j]=f[n][j]最后:
dp[1][1]即为所求
最大连续子序列
问题描述
给定一个数列A1 … An,求i,j使得Ai +… +Aj 最大,输出这个最大值。
如
-2 11 -4 13 -5 -2显然最大值为11+-4+13=20
求解
令
dp[i]表示以Ai作为末尾的连续序列最大值和,那么由于dp[i]要求必须以A[i]结尾,那么只有两种情况:
- 这个最大和的连续连续序列只有一个元素,即A[i]本身
- 这个最大和连续序列有多个元素,即从前面A[p]开始,一直到A[i]结尾。此时最大和为
dp[i-1] + A[i]所以得到状态转移方程:
dp[i]=max(A[i], dp[i-1]+A[i])边界:
dp[0] = A[0]
最长不下降子序列LIS
longest increasing sequence
问题描述
在一个数字序列中,找到一个最长的子序列(可以不连续),使得这个子序列是不下降的(非递减的)。
如
1 2 3 -1 -2 7 9,它的最长不下降子序列是1 2 3 7 9长度为5。
求解
令dp[i]为以Ai作为结尾的最长不下降子序列长度。则有两种情况:
- 如果存在A[i] 之前的元素 A[j]使得(j < i),使得A[j]<= A[i]且
dp[j]+1 > dp[i](即以Aj结尾的LIS,再加上Ai构成了一个新的LIS),那么就令dp[i]=dp[j+1]+1- 如果A[i]之前的元素都比A[i]大,那么A[i]就自己形成了一个LIS,dp[i]=1
所以可得状态转移方程:
dp[i]=max(dp[j]+1,1)(j=1..i-1 && A[j]<=A[i])边界:
dp[0]=1, dp[i]>=1
最长公共子序列LCS
longest common subsequence
问题描述
字符串A,B,求一个字符串,使得这个字符串是A,B的最长公共部分。如"sadstory"与"adminsorry"的最长公共子序列为"adsory"
求解
令
dp[i][j]表示字符串A的i号位和字符串B的j号位之前的LCS长度(下标从1开始),如dp[4][5]表示"sads"与“admin”的LCS长度。那么可以根据A[i] 、B[j]的情况,分为两种决策:
- 若
A[i]==B[j],则字符串A与B的LCS增加一位,即有dp[i][j]=dp[i-1][j-1]+1。如dp[4][6]表示"sads"与“admins”的LCS长度,由于A[4]==B[6]所以dp[4][6]=dp[3][5]+1- 若
A[i]!=B[j],则字符串A的i号位与字符串B的j号位之前的字符串无法延长,因此dp[i][j]=max{dp[i-1][j],dp[i][j-1]}。所以可得状态转移方程:
dp[i][j]=dp[i-1][j-1],A[i]==B[j] dp[i][j]=max(dp[i-1][j],dp[i],[j-1]),A[i]!=B[j]边界条件:
dp[i][0]=dp[0][j]=0最终
dp[lenA][lenB]就是LCS的长度。
最长回文子串
问题描述
给出一个字符串S,求S的最长回文字符串的长度。
例如:“patzjujztaccbcc”的最长回文字符串为“atzjujzta”长度为6
求解
令
dp[i][j]表示S[i]到S[j]所表示的字串是否为回文子串,是则是1,不是则是0。这样根据s[i]是否等于s[j]可以把问题分为2类:
- 若s[i]==s[j],那么只要s[i+1]至s[j-1]是回文字符串,那么s[i] 至 是s[j]就是回文子串;如果s[i+1]至s[j-1]不是回文字符串,则s[i] 至s[j]也不是回文字符串。
- 若s[i]!=s[j],那么s[i]至s[j]肯定不是回文字符串。
所以可以得到状态转移方程:
dp[i][j]=dp[i+1][j-1],s[i]==s[j] dp[i][j]=0,s[i]!=s[j]边界条件:
dp[i][i]=1,dp[i][i+1]=(S[i]==S[i+1])?1:0
怎么遍历?
边界条件为长度为1,2的子串;只有长度为2的子串的dp求出来之后才能得到长度为3的子串的dp。所以按照长度遍历最合适。
for(int L = 3;L<=len;L++){
for(int i=0;i+L-1 <len; i++){
int j = i + L -1;// 子串的右端点
if(s[i] == s[j] && dp[i+1][j-1] == 1){
dp[i][j]=1;
ans = L;
}
}
}
0 1 背包问题
问题描述
有n件物品,每间的重量为w[i],价值为c[i]。现在有一个容量为V的背包,问如何选取物品放入背包,使得背包内的总价值最大。其中每种物品只有一件。
样例
n=5, V=8
3 5 1 2 2 //w[i]
4 5 2 1 3 //c[i]
求解
令
dp[i][v]表示前i件物品(1≤i≤n),恰好装入容量为v的背包中所能获得的最大价值。两种策略:
- 不放第i件物品,则问题转换为前i-1件物品恰好装入容量为v的背包中所能获得的最大价值。此时
dp[i][v]=dp[i-1][v]- 放第i件物品,则问题转换为前i-1件物品恰好转入容量为v-w[i]的背包中所能获得的最大价值。此时
dp[i][v]=dp[i-1][v-w[i]+c[i]所以可得状态转移方程:
dp[i][v]=max{ dp[i-1][v],dp[i-1][v-w[i]+c[i]} 1≤i≤n, w[i]≤v≤V边界:
dp[0][v]=0这样时间空间复杂度都为O(nV);
优化
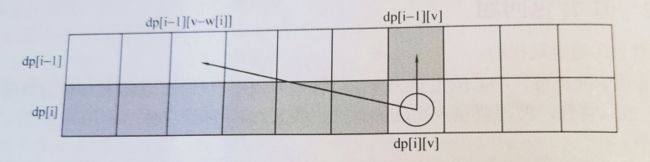
注意到计算dp[i][v]时总是需要dp[i-1][v]和其左侧部分的数据,且完全不需要i-2的数据,所以可以开一个一维数组,这样状态转移方程变成了:dp[v]=max(dp[v],dp[v-w[i]] + c[i]) 1≤i≤n, w[i]≤v≤V,枚举方向改变为i从1-n,v 从 V 到0。
为什么从V到0? 因为,要求d[v],需要用到之前已经求好的上一层求得d[v-w[i]] 这个数据,这个数据实在d[v]之前得,如果从小到大遍历,会先把d[v-w[i]]这个数据给覆盖掉,然后才遍历到d[v]
核心代码
for(int i = 0; i <= V; i ++){
dp[v]=0;
}
for(int i = 1; i <= n; i ++){
for(int v = V; v >= w[i]; v --){
dp[v]=max(dp[v],dp[v-w[i]] + c[i])
}
}
完全背包问题
问题描述
和01背包问题一样,就是每件物品可以放很多次了。
求解
令
dp[i][v]表示前i件物品(1≤i≤n),恰好装入容量为v的背包中所能获得的最大价值。两种策略:
- 不放第i件物品,则问题转换为前i-1件物品恰好装入容量为v的背包中所能获得的最大价值。此时
dp[i][v]=dp[i-1][v]- 放第i件物品,则问题转换为前i件物品恰好转入容量为v-w[i]的背包中所能获得的最大价值。此时
dp[i][v]=dp[i][v-w[i]+c[i](因为还可以接着放第i件物品)所以可得状态转移方程:
dp[i][v]=max{ dp[i-1][v],dp[i][v-w[i]+c[i]} 1≤i≤n, w[i]≤v≤V边界:
dp[0][v]=0
优化
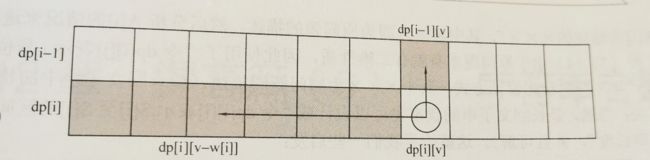
注意到计算dp[i][v]时总是需要dp[i][v]和其左侧部分的数据,且完全不需要i-2的数据,所以可以开一个一维数组,这样状态转移方程变成了:dp[v]=max(dp[v],dp[v-w[i]] + c[i]) 1≤i≤n, w[i]≤v≤V 但是枚举方向是从w[i]到V。
为什么从w[i]到V(即是从前到后)? 因为d[v] 是根据本层d[v-w[i]]和上层d[v]确定的,要先确定好之前的状态才好求d[v];
核心代码
for(int i = 0; i <= V; i ++){
dp[v]=0;
}
for(int i = 1; i <= n; i ++){
for(int v = V; v >= w[i]; v --){
dp[v]=max(dp[v],dp[v-w[i]] + c[i])
}
}
docker run -d \
-v /root/nextcloud/html:/var/www/html \
-v /root/nextcloud/apps:/var/www/html/custom_apps \
-v /root/nextcloud/config:/var/www/html/config \
-v /root/nextcloud/nextcloud/data:/var/www/html/data \
-v /root/nextcloud/themes:/var/www/html/themes \
-p 80:80 \
--restart always \
--name nextcloud \
nextcloud:17-apache
docker run -d -v ~/docker/nextcloud:/var/www/html -p 11180:80 --name nextcloud --restart always nextcloud
docker run -d -p 11280:80 --name onlyoffice --restart always onlyoffice/documentserver
KMP 算法
给定2个字符串text,和pattern 判断pattern是否为text的子串,如text=“ababababa” 则 “aba” 就是text的子串。
暴力算法:
枚举text的起始位置i,然后从该位置开始逐位于模式串pattern进行匹配,如果匹配过程中,每一位都相等,则匹配成功,否则,只要出现某位不相等,就让text串的起始位置变为i+1,并从头开始于模式串进行匹配。时间复杂度为O(nm);
KMP算法
使用kmp算法的时间复杂度可以降低为O(nm);
next数组求法
见算法笔记p457
int next[m]; m为pattern的长度。
next[i]表示使子串s[0…i] 的前缀等于后缀 s[i-k…i]的最大k, 也就是所求最长相等前后缀中前缀最后一位下标。如果找不到则next[i] = -1
如:对于pattern=“ababaab”;
对于i=0 ,子串 “a”,找不到相等的前后缀(前后缀不能是子串本身),所以next[0]=-1(对于其他串next[0]也一定是-1)。
对于i=1,子串"ab",找不到相等的前后缀,next[1]=-1。
对于i=2,子串"aba", 找到相等的前后缀“a”,所以next[2]=0;
对于i=3, 子串"abab",相等前后缀为"ab",所以next[3]=1;
对于i=4,子串"ababa",相等的前后缀"aba“,所以next[4]=2;
对于i=5,子串"ababaa" ,next[5]=0
求解next数组的算法
- 初始化next 数组,令j = next[0] = -1
- 让i再1~len-1范围遍历,对于每个i,执行3,4
- 不断令j = next[j],直到j 回退到 -1, 或者 s[i] == s[j + 1]成立
- 如果s[i] == s[j + 1], 则next[i] = j + 1; 否则 s[i] = j (此时j 一定是-1)
int next1[100];
//
void getNext(char s[], int len){
int j = -1;
next1[0] = -1;
for (int i = 1; i < len; ++i) {
while (j != -1 && s[i] != s[j + 1]){
j = next1[j];
}
if(s[i] == s[j + 1]){
j ++;
}
next1[i] = j;
}
}
kmp进行模式匹配
算法思路:(要先求好pattern地next)
- 初始化j=-1, 表示pattern当前已被匹配的最后一位
- 让i遍历文本串text,对每个i执行,3,4
- 不断地令j=next[j]直到 j==-1 或者 text[i] == pattern[j + 1]
- 如果text[i] == pattern[j + 1],则令j ++,如果j达到 len(pattern) - 1,说明pattern 匹配成功,返回true
- 返回false
bool kmp(char text[] , char pattern[]){
int n = strlen(text);
int m = strlen(pattern);
int j = -1;
for (int i = 0; i < n; ++i) {
while (j != -1 && text[i] != pattern[j + 1] ){
j = next1[j];
}
if(text[i] == pattern[j + 1]){
j ++;
}
if(j == m - 1){
return true;
}
}
return false;
}
使用kmp匹配字符串出现的次数:
/**
* 获得pattern再text中出现的次数
* @return
*/
int kmpGetPatternNum(char text[], char pattern[]){
int n = strlen(text), m = strlen(pattern);
int ans = 0;
int j = -1;
for (int i = 0; i < n; ++i) {
while (j != -1 && text[i] != pattern[j + 1]){
j = next1[j];
}
if(text[i] == pattern[j + 1]){
j ++;
}
if(j == m - 1){//匹配成功一次
ans ++;
j = next1[j];
}
}
return ans;
}
分块思想
对于一个问题:给出一个非负整数序列A,实时查询序列元素第K大的元素。一般来说在查询过程中元素个数可能会发生变化(如,插入,删除)等,就说这种查询为在线查询。如果使用暴力算法,在添加和删除时,就要有O(n)的时间复杂度来移动元素。
如果使用分块的话,只需要O(2logn)的时间复杂度:
对于有N个元素的有序序列来说,除了最后一个块,每块元素个数都应该为logn (向下取整),这样就把n个元素的序列分成了logn(向上取整块),如 11个元素,可以分成4块,块元素个数为 3 3 3 2;
一般来说序列中元素都是不超过10^5的非负整数, 可以设置一个hash数组,table[100001],table[x]代表元素当前序列A中的个数;接着将0~10^5 分为 317块,其中每块元素个数为316。定义一个block[316](317也可)数组,block[i]表示,第i块上元素的个数。
如果要新增加一个元素x, 就可以先求得其所在的块号,block[x / 316] ++, 表示对应块上的元素多了一个,同时table[x] ++, 表示像x这样大的元素多了一个。
这样以来,查询思路:先用O(logn)的时间找到第K大的元素在哪个快,然后再用O(logn)的时间在对应块中找到这个元素。时间复杂度为O(logn)。
代码如下
const int maxn = 100010;
const int sqrN = 316; //sqrt(100010)线下取证,表示块内元素
stack st;
int block[sqrN];//记录每一个块中的元素个数
int table[maxn]; //hash数组,hash[i]记录元素在当前序列中存在的个数
//找到现存数列中第K大的数
void peekMedian(int K) {
int sum = 0; //sum存放当前累计存在的个数
int idx = 0; //块号
while (sum + block[idx] < K) {
sum += block[idx++];
}
//此时 第K大的数一定在idx块号中
int num = idx * sqrN;//idx 号块中的第一个元素
while (sum + table[num] < K) {
sum += table[num++];
}
//此时 sum < K , 但是 sum + num的个数 > K, 说明num就是第K大的数
printf("%d\n", num);
}
//向序列--栈中加入x 这个数
void push(int x) {
st.push(x);
//x所在的块 里面元素个数++
block[x / sqrN]++;
table[x]++; //x的个数加一
}
void pop() {
int x = st.top();
st.pop();
block[x / sqrN]--;//x所在块的元素减一
table[x]--;
printf("%d\n", x);
}
例题
对栈来说,PeekMedian操作是指查看栈中中间大的那个数,假设栈中有n个数字,如果n为偶数,则输出第n/2 大的数,如果为奇数,输出(N+1)/2大的数。
输入
第一行,是操作的个数N, N不大于10^5,接下来N行是3中操作中的一个:
Push key
Pop
PeekMedian
key也不大于10^5。
输出
如果push,则把push进栈,如果是操作pop,则将栈顶元素输出,并出栈,如果是PeekMedian,则查看中间大的那个数。如果栈为空,操作为pop,或PeekMedian 输出Invalid。每个输出占一行。
Sample Input
17
Pop
PeekMedian
Push 3
PeekMedian
Push 2
PeekMedian
Push 1
PeekMedian
Pop
Pop
Push 5
Push 4
PeekMedian
Pop
Pop
Pop
Pop
sample output
Invalid
Invalid
3
2
2
1
2
4
4
5
3
Invalid
#include
#include
#include
using namespace std;
const int maxn = 100010;
const int sqrN = 316; //sqrt(100010)线下取证,表示块内元素
stack st;
int block[sqrN];//记录每一个块中的元素个数
int table[maxn]; //hash数组,hash[i]记录元素在当前序列中存在的个数
//找到现存数列中第K大的数
void peekMedian(int K) {
int sum = 0; //sum存放当前累计存在的个数
int idx = 0; //块号
while (sum + block[idx] < K) {
sum += block[idx++];
}
//此时 第K大的数一定在idx块号中
int num = idx * sqrN;//idx 号块中的第一个元素
while (sum + table[num] < K) {
sum += table[num++];
}
//此时 sum < K , 但是 sum + num的个数 > K, 说明num就是第K大的数
printf("%d\n", num);
}
//向序列--栈中加入x 这个数
void push(int x) {
st.push(x);
//x所在的块 里面元素个数++
block[x / sqrN]++;
table[x]++; //x的个数加一
}
void pop() {
int x = st.top();
st.pop();
block[x / sqrN]--;//x所在块的元素减一
table[x]--;
printf("%d\n", x);
}
int main() {
int x, query;
memset(block, 0, sizeof(block));
memset(table, 0, sizeof(table));
char cmd[20];// 命令
scanf("%d", &query);
for (int i = 0; i < query; ++i) {
scanf("%s", cmd);
if (cmd[1] == 'u') { //push
scanf("%d", &x);
push(x);
} else if (cmd[1] == 'o') {//pop
if (st.empty()) {
printf("Invalid\n");//站空
} else {
pop();
}
}else{ //peekMedian
if(st.empty()){
printf("Invalid\n");//站空
}else {
int K = st.size();
if(K % 2 == 0){ //偶数
K /= 2;
}else {
K = (K + 1) / 2;
}
peekMedian(K);
}
}
}
}
树状数组
lowbit运算
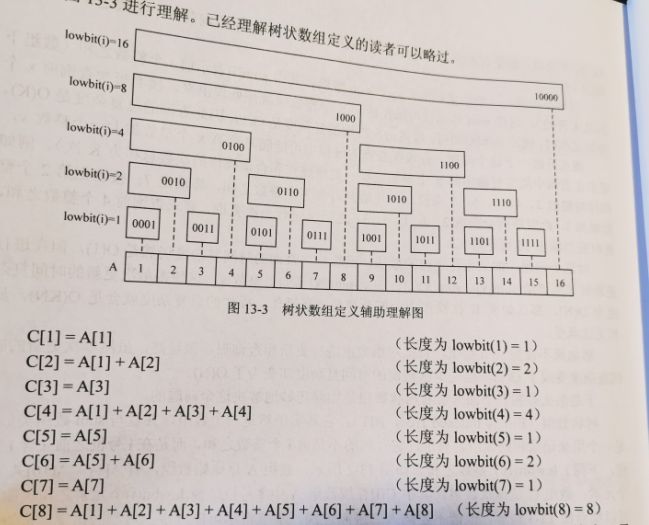
定义lowbit(x) = x & (-x) , 整数在计算机中一般用补码表示,补码等于x的反码+1,例如 6 = (0110)2 (假设最高位是符号位)其补码就是 (1010)2 , 同理 -6=(1110)2的补码就是 (0010)2,所以lowbit(6) = 2。
容易得到:lowbit(x) 就是取x二进制码最右边的1,和它右边的所有0。如x=7=(111)2则lowbit(7) = 1,lowbit(10) = 4 。
树状数组
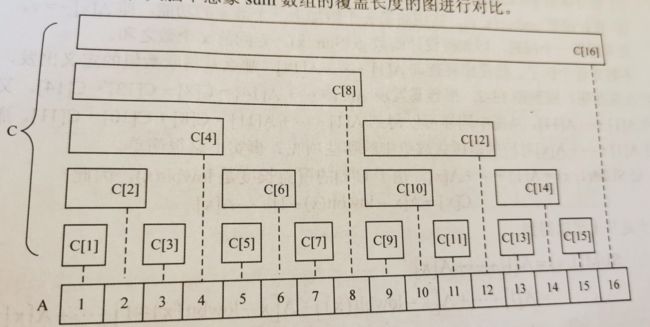
假设A是原始数组,A[1]~A[16] 共有16个元素(下标必须从1开始),定义数组C是树状数组,则C[i],存放在i号位之前的元素和,包括第i位。如C[6] = A[5] + A[6]。
解决的问题
- 设计函数getSum(x), 实现返回前x个数之和A[1] + … A[x]。
- 设计一个update(x, v), 实现将第x个数加上v的功能,即A[x] + v。
易得:
C[x] = A[x - lowbit[x] + 1] +… A[x]
所以:
sum(1, x) = A[1] + A[2] + …A[x]
= A[1] + … + A[x-lowbit(x)] + A[x - lowbit(x) + 1] + … + A[x]
= sum(1, x-lowbit(x)) + C[x]
所以易得代码:
#define lowbit(i) ((i) & (-i))
//获取前x个整数之和
int getSum(int x){
int sum = 0;
for (int i = x; i > 0 ; i -= lowbit(i)) {
sum += c[i];
}
return sum;
}
i - lowbit(i) 是个啥?i = i - lowbit(i)实际上是不断把i 的二进制最右边的1,置为0 的过程。 所以for 循环的次数,就是x 二进制中1的次数。所以getSum(x)的时间复杂度至多为O(logn);
如果要求数组下标[x, y] 之内的核, 只需要求getSum(y) - getSum(x-1)即可
第二个问题:
假设A[6] 增加 v, 数组C 怎么变化? 由上图易得,C[6] C[8] C[16] 都要加上v,因为他们的和都覆盖了A[6]。
那么C[x] 如何找到最近能覆盖C[x]的C[y]呢(C[6]找C[8])?
首先这个数肯定比x大(如果y比x小,C[y]覆盖的值中不可能含有A[x]);所以这个问题等价于求一个尽可能小的数a,使得 lowbit(a + x) > lowbit(x)。
显然, 如果lowbit(a) < lowbit(x), lowbit(a + x) < lowbit(x) (可以换算成2进制看看)。所以lowbit(a) 不能小于lowbit(x)。那么a 可以取 lowbit(x),此时a的最后一个1,和x的最后一个1,是在同一位上,相加之后的lowbit一定大于lowbit(x),即lowbit(x + lowbit(x)) > lowbit(x)。
所以update函数只需要让x不断加上lowbit(x),然后让每一步C[x] 都加上v, 即可。代码如下:
//将数组中A[x] 加上v
void update(int x, int v){
for (int i = x; i <= N; i += lowbit(i)) {
c[i] += v;
}
}
同理,update函数的时间复杂度也是log(n)
例题
问题描述:
给定一个有N个正整数的序列A,求出序列中它左边比他小的数的个数。
如{2,5,1,3,4}则应该输出{0,1,0,2,3}
思路
使用一个hash数组,hash[x] 表示当前序列 x 出现的次数。从左到右遍历A,令hash[A[i]] ++, 此时序列中比A[i] 小的个数等于 hash[1] + … + hash[A[i] - 1]。
所以可以设置一个树状数组C,初始C里面元素都为0,因为hash里面的元素都为0。hash[A[i]] ++, 可以使用 update(A[i], 1)代替,而hash[1] + … + hash[A[i] - 1] 可以使用 getSum(A[i] - 1)代替。
#include
#define lowbit(i) ((i) & (-i))
const int N = 10010;
int c[N]; //C的大小位hash数组的大小,即题目出现的最大值
//获取前x个整数之和
int getSum(int x){
int sum = 0;
for (int i = x; i > 0 ; i -= lowbit(i)) {
sum += c[i];
}
return sum;
}
//将数组中A[x] 加上v
void update(int x, int v){
for (int i = x; i <= N; i += lowbit(i)) {
c[i] += v;
}
}
int main() {
int a[5] = {2,5,1,3,4};
for (int i = 0; i < 5; ++i) {
update(a[i], 1); //表示a[i] 出现的次数+1
//此时左边a[i]左边 比a[i] 小的数的个数为
printf("%d ", getSum(a[i] - 1));
}
}
如果统计在元素左边比该元素大的元素,等价于求hash[A[i] + 1] + … hash[N],于是至于要求getSum(N) - getSum(A[i]) 就可以了。
改进: 离散化
如果A[i] 过大怎么办? 其实对于上面的问题来说,{99999999,15,6666,88888} 和 {4,1,2,3}是一样的。
此时可以定义一个临时数组A保存,原数组的列表排名。(从1,开始)
struct {
int value; //原始值
int pos; //原始的顺序
}temp[n]
int A[n]; //记录
int main(){
for(int i = 0; i < n; i ++){
temp[i].value = orgin[i];
temp[i].pos = i;//原始序号
}
sort(temp, temp +n ,cmp);//按照value,从小到打排序
for(int i = 0; i < n; i ++){
if(i == 0|| temp [i].value != temp[i-1].value){
A[temp[i].pos] = i + 1;
}else {
A[temp[i].pos] = A[temp[i-1].pos];
}
}
//后面的就和上面一样了
}
例题2
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
提示:
0 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self
这一题可以使用树状数组来解决,只需要从后往前遍历即可,然后将得到的数,放到结果列表的第一位。由于nums[i] 的值可能为赋值,所以可以使用离散化来处理。
package lowbit;
import lombok.val;
import org.junit.Test;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
/**
* @author TylerChen
* @date 2020/12/31 - 12:59
*/
public class Leetcode315 {
int lowbit(int x){
return x & -x;
}
int []A; //离散化后的数组,保留的是排名
int []C; //树状数组
static class Node {
int val, pos;
Node(int val, int pos){
this.val = val;
this.pos = pos;
}
}
/**
* 获取hash[1] + ... hash[x]的值
* @param x
* @return
*/
int getSum(int x){
int sum = 0;
for (int i = x; i > 0 ; i -= lowbit(i)) {
sum += C[i];
}
return sum;
}
/**
* hash[x] += v
* @param x
* @param v
* @return
*/
void update(int x, int v){
for (int i = x; i < C.length ; i += lowbit(i)) {
C[i] += v;
}
}
public List<Integer> countSmaller(int[] nums) {
Node[] nodes = new Node[nums.length];
A = new int[nums.length + 1];
C = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
nodes[i] = new Node(nums[i], i);
}
Arrays.sort(nodes, (a,b)-> a.val - b.val); //从小到达进行排序
for (int i = 0; i < nodes.length; i++) {
if(i == 0 || nodes[i].val != nodes[i - 1].val){
A[nodes[i].pos] = i + 1; //排名从1开始
}else {
A[nodes[i].pos] = A[nodes[i - 1].pos]; //和上一个的排名一样
}
}
LinkedList<Integer> res = new LinkedList<>();
for (int i = A.length - 2; i >= 0 ; i--) {
update(A[i],1);//A出现加一次
res.addFirst(getSum(A[i] - 1));
}
return res;
}
@Test
public void test(){
System.out.println(countSmaller(new int[]{
5,2,6,1}));
}
}
使用树状数组解决第当前序列中第K大的数
逻辑的hash[x] 表示x出现的次数,那么序列第k大,就是使得hash[1] + … hash[i] >= k 成立的最小i。可以使用二分法查找。
int findKthElement(int k){
int l = 1, r = maxn, mid;
while(l < r){
mid = (l + r) / 2;
if(getSum(mid) >= k){
r = mid;
}else {
l = mid + 1;
}
}
return l;
}
扩展
扩展到二维
如果求A[1][1] ~ A[x][y]这个子矩阵的所有元素和,以及给单点A[x][y]加上整数v? 做法一样,
void update(int x, int y, int v){
for(int i = x; i < maxn; i += lowbit(i)){
for(int j = y; j < maxn; j += lowbit(j) ){
c[i][j] += v;
}
}
}
`A[1][1] ~ A[x][y]`这个子矩阵的所有元素和
int getsum(int x, int y){
int sum = 0;
for(int i = x; i > 0; i -= lowbit(i)){
for(int j = y; j > 0; j -= lowbit(j)){
sum += c[i][j];
}
}
return sum;
}
bit(i)) {
c[i] += v;
}
}
int main() {
int a[5] = {2,5,1,3,4};
for (int i = 0; i < 5; ++i) {
update(a[i], 1); //表示a[i] 出现的次数+1
//此时左边a[i]左边 比a[i] 小的数的个数为
printf("%d ", getSum(a[i] - 1));
}
}
如果统计在元素左边比该元素大的元素,等价于求hash[A[i] + 1] + .... hash[N],于是至于要求getSum(N) - getSum(A[i]) 就可以了。
## 改进: 离散化
如果A[i] 过大怎么办? 其实对于上面的问题来说,{99999999,15,6666,88888} 和 {4,1,2,3}是一样的。
此时可以定义一个临时数组A保存,原数组的列表排名。(从1,开始)
```c++
struct {
int value; //原始值
int pos; //原始的顺序
}temp[n]
int A[n]; //记录
int main(){
for(int i = 0; i < n; i ++){
temp[i].value = orgin[i];
temp[i].pos = i;//原始序号
}
sort(temp, temp +n ,cmp);//按照value,从小到打排序
for(int i = 0; i < n; i ++){
if(i == 0|| temp [i].value != temp[i-1].value){
A[temp[i].pos] = i + 1;
}else {
A[temp[i].pos] = A[temp[i-1].pos];
}
}
//后面的就和上面一样了
}
例题2
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
提示:
0 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self
这一题可以使用树状数组来解决,只需要从后往前遍历即可,然后将得到的数,放到结果列表的第一位。由于nums[i] 的值可能为赋值,所以可以使用离散化来处理。
package lowbit;
import lombok.val;
import org.junit.Test;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
/**
* @author TylerChen
* @date 2020/12/31 - 12:59
*/
public class Leetcode315 {
int lowbit(int x){
return x & -x;
}
int []A; //离散化后的数组,保留的是排名
int []C; //树状数组
static class Node {
int val, pos;
Node(int val, int pos){
this.val = val;
this.pos = pos;
}
}
/**
* 获取hash[1] + ... hash[x]的值
* @param x
* @return
*/
int getSum(int x){
int sum = 0;
for (int i = x; i > 0 ; i -= lowbit(i)) {
sum += C[i];
}
return sum;
}
/**
* hash[x] += v
* @param x
* @param v
* @return
*/
void update(int x, int v){
for (int i = x; i < C.length ; i += lowbit(i)) {
C[i] += v;
}
}
public List<Integer> countSmaller(int[] nums) {
Node[] nodes = new Node[nums.length];
A = new int[nums.length + 1];
C = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
nodes[i] = new Node(nums[i], i);
}
Arrays.sort(nodes, (a,b)-> a.val - b.val); //从小到达进行排序
for (int i = 0; i < nodes.length; i++) {
if(i == 0 || nodes[i].val != nodes[i - 1].val){
A[nodes[i].pos] = i + 1; //排名从1开始
}else {
A[nodes[i].pos] = A[nodes[i - 1].pos]; //和上一个的排名一样
}
}
LinkedList<Integer> res = new LinkedList<>();
for (int i = A.length - 2; i >= 0 ; i--) {
update(A[i],1);//A出现加一次
res.addFirst(getSum(A[i] - 1));
}
return res;
}
@Test
public void test(){
System.out.println(countSmaller(new int[]{
5,2,6,1}));
}
}
使用树状数组解决第当前序列中第K大的数
逻辑的hash[x] 表示x出现的次数,那么序列第k大,就是使得hash[1] + … hash[i] >= k 成立的最小i。可以使用二分法查找。
int findKthElement(int k){
int l = 1, r = maxn, mid;
while(l < r){
mid = (l + r) / 2;
if(getSum(mid) >= k){
r = mid;
}else {
l = mid + 1;
}
}
return l;
}
扩展
扩展到二维
如果求A[1][1] ~ A[x][y]这个子矩阵的所有元素和,以及给单点A[x][y]加上整数v? 做法一样,
void update(int x, int y, int v){
for(int i = x; i < maxn; i += lowbit(i)){
for(int j = y; j < maxn; j += lowbit(j) ){
c[i][j] += v;
}
}
}
`A[1][1] ~ A[x][y]`这个子矩阵的所有元素和
int getsum(int x, int y){
int sum = 0;
for(int i = x; i > 0; i -= lowbit(i)){
for(int j = y; j > 0; j -= lowbit(j)){
sum += c[i][j];
}
}
return sum;
}