二叉平衡树 python 列表 递归

二叉平衡树-python-列表-递归

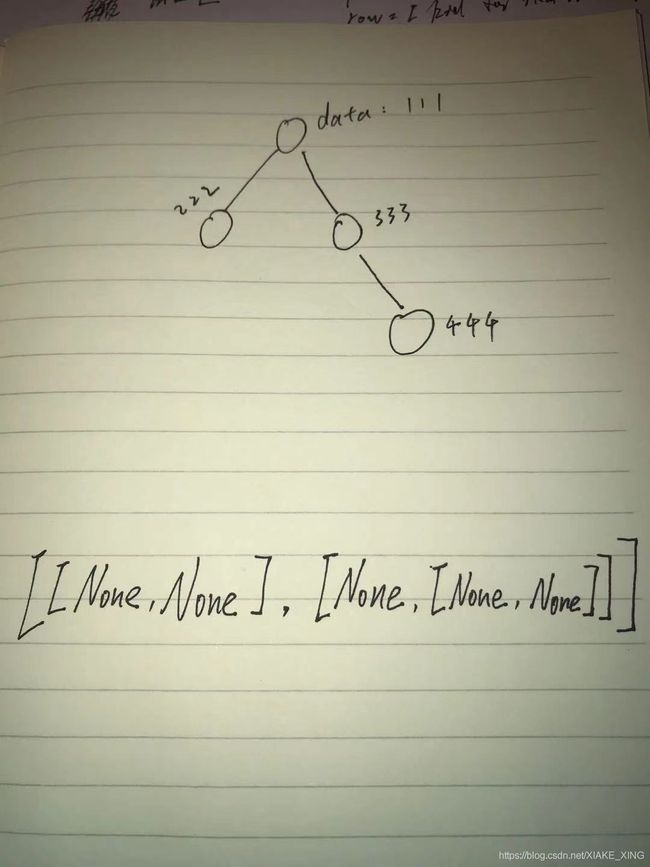
用列表递归的方式表示二叉树，例如：只有根root的树用列表来表示就是 [None, None], 再例如一个这样的树：

用列表来表示就是：
[[None, None, 222], [None, [None, None, 444], 333], 111]
可以简单的认为看见一个 ‘ [ ] ’ 括号就认为它是一个节点，里面的元素有该节点的左kid，右kid，以及这个节点的data.

所以，我构建了一个这样的树结构：

class Node(object):
    def __init__(self, data=None, l_kid=None, r_kid=None):
        self.data = data
        self.left = l_kid
        self.right = r_kid


class Tree(object):
    list_with_node = None   # 例 ：只有根的二叉树为 [None, None, root]
    list_only = None        # 例 ：只有根的二叉树为 [None, None]
    list_with_data = None   # 例 ：只有根的二叉树为 [None, None, root.data]

    def __init__(self, root=None):
        self.root = root

    # 例：[None, None, root]表示一个只有root节点的树,有三个元素:左子树,右子树,该节点对象
    def list_with_node_travel(self, node):
        if not node:
            return None
        total = [
            self.list_with_node_travel(node.left),
            self.list_with_node_travel(node.right),
            node,
        ]
        return total

    # 例：[None, None]表示一个只有root节点的树, [[None, None], [None, None]]表示一个第三层全为None的平衡树
    def list_only_travel(self, node):
        if not node:
            return None
        total = [
            self.list_only_travel(node.left),
            self.list_only_travel(node.right),
            # node,
         ]
        return total

    # 例：[None, None, root.data]表示一个只有root节点的树,有三个元素:左子树,右子树,该节点的data
    def list_with_data_travel(self, node):
        if not node:
            return None
        total = [
            self.list_with_data_travel(node.left),
            self.list_with_data_travel(node.right),
            node.data,
         ]
        return total

    def update_list(self):
        Tree.list_with_node = self.list_with_node_travel(self.root)
        Tree.list_only = self.list_only_travel(self.root)
        Tree.list_with_data = self.list_with_data_travel(self.root)

    # 层次遍历list，也可以说是树，当遇到第一个None时，返回None在该层的index，以及该层的深度depth
    # depth从2开始，默认root存在, 换句话说Tree.list_only默认为list类型.
    def _append(self, x, depth=2):
        if isinstance(x, list):
            if None in x:
                # 返回该层第一次出现None的index和该层的depth
                return x.index(None), depth
            # 如果该层没有None，说明该层满了，那就用循环打开x内的所有list，并把他们拼在一起
            # 这步的意思就是，进入下一层，递归判断第一次出现None的坐标
            a = []
            for i in x:
                a.extend(i)
            depth += 1
            y = depth
            return self._append(a, depth=y)

    # 传入一个node，添加在树的结构里
    def append(self, node):
        index, depth = self._append(Tree.list_only)
        code = self._arithmetic(index, depth)
        if len(code) == 1:
            # [None, None, node]为这个新node，左右子树为None, 节点对象为node.
            Tree.list_with_node[int(code)] = [None, None, node]
            # 为该node对象建立父子关系
            if int(code) == 0:
                self.root.left = node
            else:
                self.root.right = node
            return self.update_list()
        current_list = Tree.list_with_node
        last = int(code[-1])
        # 先走到这个新节点的父辈节点.
        code_to_father = code[:-1]
        for i in code_to_father:
            current_list = current_list[int(i)]
        # 此时current_list来到父节点[x, x, 父node]，这时再看最后一步的方向来设置新node为父节点的哪边。
        if last == 0:
            current_list[-1].left = node
        else:
            current_list[-1].right = node
        current_list[last] = [None, None, node]
        return self.update_list()

    # 根据depth和该层第一次出现None的index，得到一个神秘码(反映出该None在数中的坐标)
    def _arithmetic(self, index, depth):
        """
            这个算法建议画图琢磨
            (position, depth),例如(6, 4)为第4层从左到右第6个元素。该层满元素个数为2 ** (depth - 1) = 8个
            步数 = depth - 1 = 3 步
            1. 因为6 > (8 / 2),所以从root开始找该元素时第一步是走root.right
            2. 再用6 - (8 / 2) = 2, 因为 2 <= ((8 / 2) / 2),所以这步是走左边left，root.right.left
            3. 上一步得出左边后，2就不用减((8 / 2) / 2), 因为2 > (((8 / 2) / 2) / 2),所以走右边right
            4. 最后路线为：root.right.left.right总共走三步就到达该node准确位置
            5. 神秘码就为 '101' , '1'为right, '0'为left.  遍历找node或node.data时会用到神秘码
        """
        position = index + 1
        # times为步数
        times = depth - 1
        # nums为该层满元素的个数(depth为2时，该层最多2个node，第三层最多4个node)
        nums = 2 ** (depth - 1)
        i = 1
        code = ''
        while i <= times:
            if position <= nums / 2:
                magic = '0'
                nums = nums / 2
            else:
                magic = '1'
                position = position - (nums / 2)
                nums = nums / 2
            code += magic
            i += 1
        return code

我们先构建这样的树结构，看看输出：

if __name__ == '__main__':
    node_a = Node(data=111)
    node_b = Node(data=222)
    node_c = Node(data=333)
    node_d = Node(data=444)
    node_e = Node(data=555)
    node_f = Node(data=666)

    # 设置树关系
    tree = Tree(node_a)
    node_a.left = node_b
    node_b.left = node_d
    node_a.right = node_c
    node_c.left = node_e
    node_e.right = node_f
    
    tree.update_list()
    print(tree.__class__.list_with_data)
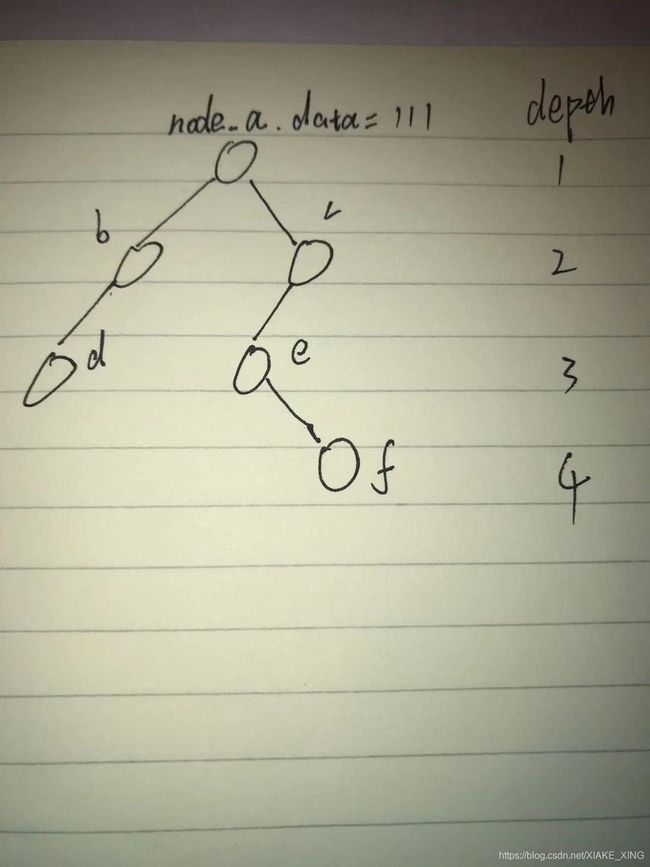
    # 输出为: [[[None, None, 444], None, 222], [[None, [None, None, 666], 555], None, 333], 111]

此输出list描述的图，画出来后就是上述的图。

可以这样去标记列表：

下面来增加几个节点来看看输出：

# append节点
    add_1 = Node(data='add_1')
    add_2 = Node(data='add_2')
    add_3 = Node(data='add_3')
    add_4 = Node(data='add_4')
    add_5 = Node(data='add_5')
    add_6 = Node(data='add_6')
    add_7 = Node(data='add_7')
    add_8 = Node(data='add_8')
    add_9 = Node(data='add_9')

    tree.append(add_1)
    tree.append(add_2)
    tree.append(add_3)
    tree.append(add_4)
    tree.append(add_5)
    tree.append(add_6)
    tree.append(add_7)
    tree.append(add_8)
    tree.append(add_9)
    print(tree.__class__.list_with_data)
# 输出为：
[[[[None, None, 'add_3'], [None, None, 'add_4'], 444], [[None, None, 'add_5'], [None, None, 'add_6'], 'add_1'], 222], [[[None, None, 'add_7'], [None, None, 666], 555], [[None, None, 'add_8'], [None, None, 'add_9'], 'add_2'], 333], 111]

此结果所描绘的树结构就是上图所示的树结构。