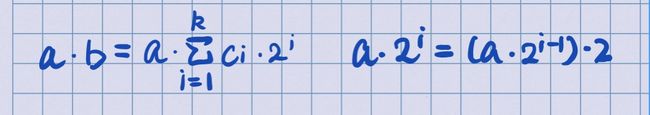算法竞赛进阶指南-0x01 位运算

大家好这里是TKLA…初学算法的大一同学~现在已经系统学习过了C语言，正在学习C++以及python…希望能在CSDN上收获到很多知识！也希望自己能成为分享知识的一员！
目前学习的教材是这本 《算法竞赛进阶指南》(李煜东 著)

---

0X00 基本算法

这本书按照 0x加上两个16进制数字组成，还是比较有趣的

---

0x01 位运算

位运算是效率最高的运算模式，充满了技巧性。

---

按位运算

位与	位或	位反	位异或
&	|	~	^

_{其中，与运算只要一端为0,结果为0，或运算只要一端为1,结果为1
异或运算当两端相异返回1否则为0}

这里介绍一下思路一致的逻辑短路(原书没有)
当运算式由或、与决定，直接返回结果，而不会看另一端
譬如，true||false 只需要看左边一端即可判断整个式子
利用这一点，我们可以卡出许多有趣的操作~

leetcode 剑指offer 64

int sumNums(int n) {
     
	int ans = n;
	(n) && (ans+=sumNums(n - 1));
return ans;}

这里使用的就是逻辑短路以替代 if 语句…毕竟递归出口还是要有 if 的
_{请大家无论如何都要去看看力扣上的大神题解！受益真的很大！}

补码、反码

这个就略去啦！不过其中有提到一个语句

memset(a,0x3f,sizeof(a));

很有用…(初始化容器)

移位运算

1 <<= n 等价于2ⁿ
n <<= 1 等价于2n

>>右移运算的向下取整机制
C语言中对于int / 2采取向0取整而不是向下取整…所以说最好是使用位运算或者是floor函数(中)

---

0x01例题一：快速幂算法(高速求解n^m%mod的值)

acwing此题

typedef long long ll;
int power(int n,int m,int mod){
     
	int ans = 1 % mod;
	for(;m;m>>=1){
     
		if(m & 1)
			ans = ll(ans)*n%mod;
		n = ll(n)*n%mod;}
return ans;}

用一张图解释下叭！

其中，可以观察到m >>= 1以及m & 1均为位运算表达，提升了效率
在这里总结一下几个

常用位运算操作：

(x & 1)	//奇数
!(x & 1)//偶数
x >>= 1		
x &= (x-1)	
	//最低位的1归0
x &= -x		
	//得到最低位的1
x & (~x) == 0

还有异或重要的两个性质:

交换数字

a ^= b ^= a ^= b;

n xor n == 0
n xor 0 == n

通过第二条性质可以推出异或前缀：

int ans_1 = arr[0],ans_2 = ans_1;
for(int m=0;m<i-1;++m)
	ans_1 ^= arr[m];
for(int m=0;m<j;++m)
	ans_2 ^= arr[m];
cout << (ans_1 xor ans_2);

也即，arr[i]^...^arr[j]可以分成两个部分来求arr[0]^...^arr[i-1]以及arr[0]^...^arrr[j]，再两式异或。
在结构上有着前缀和特征，因此被叫做前缀和性质
来做一道相关的leetcode

---

0x01例题2：64位整数乘法(求解a*b%mod的值)

acwing此题

解法一：快速幂思想 O( logn)

typedef long long ll;
ll mul(ll a,ll b,ll mod){
     
	ll ans = 0;
	for(;b;b>>=1){
     
		if(b & 1)
			ans = (ans+a)%mod;
		a = 2*a%mod;}
return ans;}

和快速幂是很像的！

---

解法二：O(1)

#define elif else if
typedef long long ll;
typedef long double ld;
ll mul(ll a,ll b,ll mod){
     
	a %= mod,b %= mod;
	ll c = ld(a)*b/mod;
	ll ans = a*b - c*mod;
	if(ans<0)
		ans += mod;
	elif(ans>=mod)
		ans -= mod;
return ans;}

这种解法…有点巧妙 _{放原文好了…}

利用 a * b mod p = a * b - [a * b / p] * p , [ ]表示向下取整

首先，当 a,b < p 时，a * b / p 下取整以后一定也小于 p。我们可以用浮点数执行 a * b / p 的运算，而不用关心小数点之后的部分。浮点类型long double在十进制下的有效数字有 18 ~ 19 位，足够胜任。当浮点数的精度不足以保存精确数值时，它会像科学计数法一样舍弃低位，正好符合我们的要求。

另外，虽然**a * b** 和 [a * b / p] * p 可能很大，但是两者的差一定在 0 ~ p - 1 之间，我们只关心它们较低的若干位即可。所以，我们可以用long long 来保存**a * b 和 [a * b / p] * p**各自的结果。整数运算溢出相当于舍弃高位，也正好符合我们的要求。

---

2进制状态压缩

将一个长度为m的bool数组使用m位二进制存储

一些相关操作：

操作	运算
取出n的第k个bit	( n >> k ) & 1
取出n的后k个bit	n & ( ( 1 << k ) - 1 )
取反n的第k个bit	n xor ( 1 << k)
将n的第k个bit置为1	n | (1 << k)
将n的第k个bit置为0	n & ( ~ ( 1 << k) )

0x01例题3: 最短Hamilton 路径

acwing此题
是一个用位运算优化复杂度的例子…
我觉得有点绕

int f[1<<20][20];//用于标记，以int 压缩 bool*
int hamilton(int n,int weight[20][20]){
     
	memset(f,0x3f,sizeof(f));
	f[1][0] = 0;
	for(int i=1;i<1<<n;++i)
		for(int j=0;j<n;++j)	
			if(i>>j & 1)
	//这个式子表示的意义：是否经过了当前状态对应的点
				for(int k=0;k<n;++k)
					if(i>>k & 1)
						f[i][j] = min(f[i][j],f[i xor 1<<j][k]+weight[k][j]);
				//i xor 1<
return f[(1<<n)-1][n-1];/*return经过所有点的状态*/}

相关题

成对变换

邻接表里的
linked to(空链接)
n xor 1 = n + 1 , n & 1 == 0
n xor 1 = n - 1 , n & 1 == 1

lowbit 运算

lowbit(n) 指的是 最低位的1以及之后的0

lowbit(n) = n & (-n)

这里简单说下，lowbit(n) = n & (~n + 1),而 ~n 其实就是 - (n+1) (补码)

应用一：Hash表

linked to(空链接)

应用二：树状数组

linked to(空链接)