【常见算法Python描述】计数排序、基数排序、桶排序简介及实现

一、计数排序

1. 简介

计数排序假定待排序列中的元素在$0$到$k$的范围内，且如果$k=O(n)$则计算排序的最坏时间复杂度为$\Theta (n)$。

计数排序的思想在于，对待排序列中的每一个元素$x$，确定比$x$小的元素个数，而后利用该信息直接将元素$x$放到输出序列的对应位置。例如：如果有$17$个元素小于$x$，则$x$为输出序列的第18个元素。

然而，实际中需要对上述方案做一定的修改，因为一般输出序列的一个位置处只有一个元素，而如果待排序列有多个相同元素，则此时上述方案无法处理这种情形。

2. 伪代码

下面给出计数排序的伪代码，其中：假定输入的待排序列为列表A[1..n]，因此A.length = n，B[1..n]为输出的有序序列，C[0..k]为辅助列表。

counting_sort(A, B, k):
	let C[0..k] be a new array
	for i = 0 to k:
		C[i] = 0
	for j = 1 to A.length:
		C[A[j]] = C[A[j]] + 1
	// 至此，C[i]包含了值等于i的元素个数
	for i = 1 to k:
		C[i] = C[i] + C[i - 1]
	// 至此，C[i]包含了值小于等于i的元素个数
	for j = A.length downto 1:
		B[C[A[j]]] = A[j]
		C[A[j]] = C[A[j]] - 1

对于上述counting_sort算法，更具体地：

• 第3至4行的for循环将序列C的所有元素初始化为0；
• 第5至6行的for循环每迭代一次都将C[i]加1，因此该for循环结束后，对于每一个$i$（其中$i=0,1,\cdot \cdot \cdot ,k$），C[i]为A中等于$i$的元素个数；
• 第8至9行的for循环结束后，C[i]为A中小于或等于$i$的元素个数；
• 第11值13行的for循环将每一个元素A[j]放置到输出的有序序列的正确位置，具体地：
  • 如果待排序列A中的$n$个元素互不相等，则C[A[j]]的值即为元素A[j]在输出序列中的最终位置；
  • 由于待排序列A中的元素可能相同，则在输出序列B中放置好某元素A[j]后，需要将C[A[j]]减1，这样一来，如果后续仍有元素等于A[j]，则该元素将会被放置到序列B中元素A[j]的前一个位置。

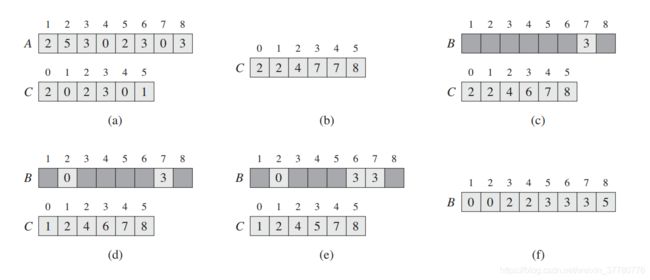
3. 图解

为使读者更好地理解上述计数排序算法counting_sort，下图描述了算法的执行过程，其中：

• 待排序列A[1..8]中的每个元素均是小于$k=5$的非负整数；
• 图$(a)$表示执行完第6行之后的待排序列A和辅助序列C；
• 图$(b)$表示执行完第9行之后的辅助序列C；
• 图$(c)$到$(e)$分别表示第11至13行的for循环分别完成1、2、3次迭代后输出序列B和辅助序列C的情况；
• 图$(f)$表示最终有序的输出序列B。

4. 代码实现

下面是计数排序的Python实现：

def count_sort(arr):
    """计数排序"""
    # 将辅助计数序列的元素全部初始化为0
    count = [0 for _ in range(256)]

    # 统计arr中每个元素的个数，且该个数值保存在count的索引arr[j]处
    for j in range(len(arr)):
        count[arr[j]] += 1

    # 使得count[i]处保存小于或等于i的元素个数
    for i in range(256):
        count[i] += count[i - 1]

    # 依次将arr中的元素放置到输出序列的有序位置处
    output = [0 for _ in range(len(arr))]
    for j in range(len(arr) - 1, -1, -1):  # 确保计数排序是稳定的
        output[count[arr[j]] - 1] = arr[j]
        count[arr[j]] -= 1

    # 切片拷贝
    arr[:] = output[:]


if __name__ == '__main__':
    arr = [2, 5, 3, 0, 2, 3, 0, 3]
    count_sort(arr)
    print(arr)  # [0, 0, 2, 2, 3, 3, 3, 5]

5. 时间复杂度

关于计数排序的时间复杂度，通过分析计数排序counting_sort的伪代码可以方便地得出，即：

• 第3至4行的for循环需要的时间为$\Theta (k)$；
• 第5至6行的for循环需要的时间为$\Theta (n)$；
• 第8至9行的for循环需要的时间为$\Theta (k)$；
• 第11至13行的for循环需要的时间为$\Theta (n)$。

综上，计数排序总的时间复杂度为$\Theta (n+k)$，而在实际中当$k=O(n)$，即待排序列的元素大小和待排序列元素个数相当，则计数排序的最坏时间复杂度为$\Theta (n)$。

二、基数排序

1. 简介

上面我们说实际中当$k=O(n)$时，计数排序的最坏时间复杂度为$\Theta (n)$，但是当$k=\Omega (n)$时，例如$k=n^2$，此时计数排序的时间复杂度为$\Theta (n^2)$，此时下面即将介绍的基数排序可能更加高效。

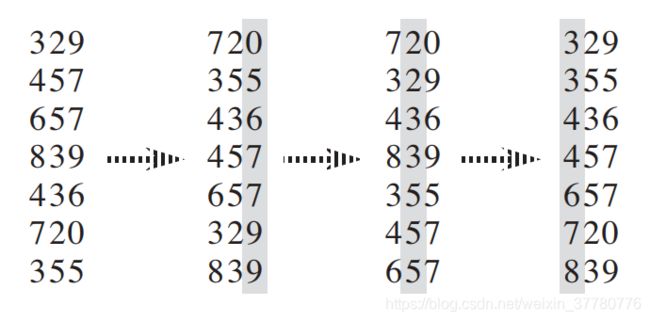
基数排序的思想很简单，以下图为例，给定7个3位数，从低位到高位开始，对其进行三轮排序，每一轮仅考虑使用当前位的数值进行排序。

2. 代码实现

对于基数排序的实现，可以使用上述计数排序来实现，因为每一轮排序中，每一位的数值都在0到9的范围内，即$k=max([0,\cdot \cdot \cdot ,9])=9$，此时计数排序可视为$\Theta (n+k)\approx \Theta (n)$。

def counting_sort(arr, exp):
    """
    按照位对arr中的元素进行计数排序
    :param arr: 待排序列
    :param exp: 指定排序位数，用10的非负整数次幂表示
    :return: None
    """

    # 初始化计数用辅助序列
    count = [0 for _ in range(10)]

    # 对于arr中的每个元素，得到其某位的值digit，并将统计得到的相同digit数量保存在count[digit]处
    for j in range(len(arr)):
        digit = (arr[j] // exp) % 10
        count[digit] += 1

    # 使得count[i]处保存小于或等于i的元素个数
    for i in range(1, 10):
        count[i] += count[i - 1]

    # 创建有序的输出序列
    output = [0 for _ in range(len(arr))]
    for j in range(len(arr) - 1, -1, -1):  # 确保计数排序是稳定的
        digit = (arr[j] // exp) % 10
        output[count[digit] - 1] = arr[j]
        count[digit] -= 1

    # 切片拷贝
    arr[:] = output[:]


def radix_sort(arr):
    """
    基数排序
    """

    # 找到待排序列中的最大值
    max_num = max(arr)

    # 从低位到高位，对待排序列依次做计数排序，其中exp表示十进制基数，
    # 如：exp = 10^0表示个位，exp = 10^1表示十位，以此类推
    exp = 1
    while max_num // exp > 0:
        counting_sort(arr, exp)
        exp *= 10


if __name__ == '__main__':
    arr = [329, 457, 657, 839, 436, 720, 355]
    radix_sort(arr)
    print(arr)  # [329, 355, 436, 457, 657, 720, 839]

3. 时间复杂度

假设给定$n$个具有$d$位的数值，且每一位最大可能为$k$，如果对每一位进行排序的算法（上述是计数排序）最坏时间复杂度为$\Theta (n+k)$，则基数排序的最坏时间复杂度为$\Theta (d(n+k))$。

三、桶排序

1. 简介

假定$n$个待排序列的元素由某随机过程产生，且每个元素均匀且独立分布于区间$[0,max(arr)]$，则桶排序的思想在于：

• 先将区间$[0,max(arr)]$分为$n$个等间隔子区间（这些子区间又被称为桶）；
• 然后将$n$个待排元素分散到对应的桶中；
• 接着对每个桶中元素进行排序（例如使用插入排序）；
• 最后从左至右按顺序将每一个桶中的元素取出合并即得有序序列。

2. 实现

def bucket_sort(arr):
    """桶排序"""
    # 确定桶的大小
    bucket_size = max(arr) / len(arr)
    # 初始化所有桶
    buckets = [[] for _ in range(len(arr))]
    # 依次将元素放入对应的桶中
    for i in range(len(arr)):
        j = int(arr[i] / bucket_size)  # 向下取整，得到元素应该被放进的桶的序号
        if j != len(arr):
            buckets[j].append(arr[i])
        else:
            buckets[len(arr) - 1].append(arr[i])

    # 对每一个桶中的元素使用插入排序
    for i in range(len(arr)):
        print(f'bucket[{i}] = {buckets[i]}')
        insertion_sort(buckets[i])

    # 将所有桶中元素顺次拼接
    result = []
    for i in range(len(arr)):
        result = result + buckets[i]
    return result


def insertion_sort(bucket):
    """插入排序"""
    for i in range(1, len(bucket)):
        current = bucket[i]
        j = i - 1
        while j >= 0 and current < bucket[j]:  # 只有同时满足条件才进行元素右移
            bucket[j + 1] = bucket[j]
            j = j - 1
        bucket[j + 1] = current  # 将元素current插入正确的位置


if __name__ == '__main__':
    arr = [12, 34, 32, 65, 76, 43, 54]
    sorted_arr = bucket_sort(arr)
    print(sorted_arr)

3. 时间复杂度

桶排序的平均时间复杂度为$\Theta (n)$。

$$T(n)=\Theta (n)+\sum _{i=0}^{n-1}O(n_i^2)$$

下面通过计算$T(n)$的数学期望来得出桶排序的平均时间复杂度：

$$\begin{array}{rl}E[T(n)]& =E\left[\Theta (n)+\sum _{i=0}^{n-1}O(n_i^2)\right]\\ & =\Theta (n)+\sum _{i=0}^{n-1}E\left[O(n_i^2)\right]\\ & =\Theta (n)+\sum _{i=0}^{n-1}O(E\left[n_i^2\right])\end{array}$$

实际上$E\left[n_i^2\right]=2-\frac{1}{n}$