JAVA-高频面试题汇总:二叉树(二)
前言
为了让小伙伴们更好地刷题,我将所有leetcode常考题按照知识点进行了归纳.
已完成:
JAVA-高频面试题汇总:动态规划
JAVA-高频面试题汇总:二叉树(一)
接下来我对树这一知识点进行归纳总结,树的内容总结了二十多道,将分为几篇文章讲解,归纳基于JAVA语言,是我一边复习一边整理的,如有疑惑欢迎交流!
小编微信: Apollo___quan
7. 树的子结构
思路
1.先遍历大树,考虑A与B,A.left与B,A.right与B
2.再遍历小树,考虑以当前node1和node2为根的树是否完全相同
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
if(A == null || B == null) return false; //题目中A和B为空则都不是子结构
return recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B); //先遍历大树,以大树节点开始进行比较,注意recur(A, B)与isSubStructure(A.left, B)的区别,一个是比较当前点,一个是往左子树右子树遍历
}
public boolean recur(TreeNode node1, TreeNode node2){
//从当前节点开始判断是否完全相同
if(node2 == null) return true; /*node2先为空说明node2遍历完了,说明是子结构。 注意判断顺序,若先判断node1==null,会出错 */ if(node1 == null || node1.val != node2.val) return false; //node2还没完node1完了,或者值不同,则false
return recur(node1.left, node2.left) && recur(node1.right, node2.right); //继续判断node1和node2的左右节点
}
}
8.二叉树的镜像
注意两种题不同,一种要求返回根节点,一种返回void,只需要交换即可
解法一(返回TreeNode)
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode leftRoot = mirrorTree(root.right);//以root.right为根,进行镜像,并返回root.right准备当作left
TreeNode rightRoot = mirrorTree(root.left);//以root.left为根,进行镜像,并返回root.left准备当作right
root.left = leftRoot; //把原来的root.right(root.right根没变,左右子树已完成镜像)赋值给root.left
root.right = rightRoot;
return root; //返回当前根节点
}
}
解法二(返回void)
public class Solution {
public void Mirror(TreeNode root) {
if (root==null) return;
if(root.left==null&&root.right==null) return;
TreeNode temp=root.right;//交换左右子树
root.right=root.left;
root.left=temp;
Mirror(root.left); //以左右子树为根,继续交换左右子树的左右子树
Mirror(root.right);
}
}
9.二叉搜索树的后序遍历序列
思路
1.后序遍历定义: [ 左子树 | 右子树 | 根节点 ] ,即遍历顺序为 “左、右、根” 。
2.数组最后一个数是根,找出从前往后数第一个大于根的数m(m记录的是小于根的个数)
3.[0,m-1]应该都小于根,[m,length-2]应该都大于根,符合该标准即为后序遍历
4.要充分考虑到无左子树或无右子树的情况,因为当无左右子树时,左界本来就已经等于右界,右界再缩小(m-1或j-1),会导致左界>右界
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if (sequence.length==0) return false;
return recur(sequence,0,sequence.length-1);
}
boolean recur(int []arr,int i,int j){
if(i>=j) return true; //这里的>需要特别注意,i是有可能>j的
int m=i;
while(arr[m]<arr[j]) m++; //m记录的是小于根的个数
int p=m;
while(arr[p]>arr[j]) p++; //当没有左子树,m=i=0,而最后recur(arr,i,m-1),i>i-1
//当没有右子树时,m=j=length-1,最后recur(arr,m,j-1),j>j-1
return p==j && recur(arr,i,m-1) && recur(arr,m,j-1);
}
}
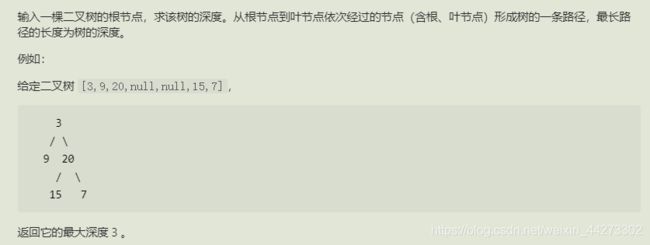
10.二叉树的深度
非常基本的题,没啥好说的,掌握好熟练度。
class Solution {
public int maxDepth(TreeNode root) {
if(root==null) return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
}
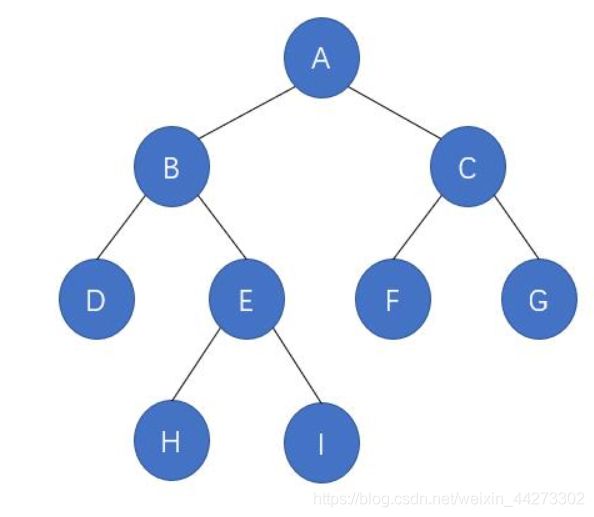
11.二叉树的下一个节点
思路
仔细观察,可以把中序下一结点归为四种类型:
-
有右子树,下一结点是右子树中的最左结点,例如 B,下一结点是 H
-
无右子树,且结点是该结点父结点的左子树,则下一结点是该结点的父结点,例如 H,下一结点是 E
-
无右子树,且结点是该结点父结点的右子树,则我们一直沿着父结点追朔,直到找到某个结点是其父结点的左子树,如果存在这样的结点,那么这个结点的父结点就是我们要找的下一结点。例如 I,下一结点是 A。
-
无右子树,且结点是该结点父结点的右子树,则我们一直沿着父结点追朔,然而找不到某个结点是其父结点的左子树,例如 G,并没有符合情况的结点,所以 G 没有下一结点
其中3、4代码可以合并成一种 (pNode.next!=null && pNode.next.left==pNode)
/* public class TreeLinkNode { int val; TreeLinkNode left = null; TreeLinkNode right = null; TreeLinkNode next = null; TreeLinkNode(int val) { this.val = val; } } */ public class Solution { public TreeLinkNode GetNext(TreeLinkNode pNode) { if(pNode==null) return null; if(pNode.right != null){ //第一种情况 TreeLinkNode cur = pNode.right; while(cur.left != null) { cur = cur.left; } return cur; } else{ if(pNode.next!=null && pNode.next.left==pNode){ //第二种情况,注意pNode.next!=null return pNode.next; } else{ TreeLinkNode node2=pNode; while(node2.next!=null&&node2!=node2.next.left) //包含了第三第四种情况 { node2=node2.next; } return node2.next; } } } }
12.对称二叉树
思路
重点是要讨论left.left,right.right 以及left.right,right.left 所以最好把左右子树拿来做递归函数的参数
boolean isSymmetrical(TreeNode pRoot)
{
if(pRoot == null) return true; //空树为true
return duicheng(pRoot.left, pRoot.right); //从左右子树单独递归,这个思路要牢记
}
public boolean duicheng(TreeNode left, TreeNode right){
if(left==null&&right==null) return true; //判空要放前面,否则后面会空指针
if(left==null||right==null||left.val!=right.val) return false;//判空要放前面,否则后面会空指针
return duicheng(left.left,right.right)&&duicheng(left.right,right.left);
}