使用遗传算法解决N皇后问题

N皇后问题

经典的N皇后问题最初被称为八皇后拼图，起源于国际象棋。任务是将八名皇后放置在棋盘上，而且他们中的任何两个都不互相构成威胁。换句话说，没有两个皇后可以在同一行、同一列或同一对角线。概括而言，N皇后问题使用N×N的棋盘和N（其中N>3）个皇后。
对于原始的八皇后情形，有92个解，消除对称解，则有12个唯一解。
使用排列组合，将8个皇后放置在8×8棋盘上的所有可能方式有4,426,165,368种。但是，如果通过确保不会在同一行或同一列上放置两个皇后的方式创建候选解决方案，则可能的组合数量将减少到$8!=40320$个。

解的表示

在解决N皇后问题时，利用以下前提条件：每行恰好容纳一个皇后，同时没有两个皇后共享同一列。这意味着可以将候选解表示为有序的整数列表或索引列表，每个索引表示皇后之一占据当前行的列数。
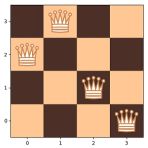
例如，在4×4棋盘上的四皇后问题中，具有以下索引列表：
(3, 2, 0, 1)
表示（索引从0开始计数）：

1. 在第一行中，皇后放置在第四列中。
2. 在第二行中，皇后放置在第三列中。
3. 在第三行中，皇后放置在第一列中。
4. 在第四行中，皇后放置在第二列中。
   下图描述了上述索引：
   
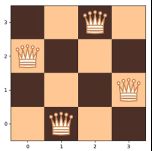
   而索引(1, 3, 0, 2)则可以用来表示下图：
   

以这种方式表示的候选解中唯一可能的违反约束的是一对皇后之间共享对角线。
如，在第一个候选解中：

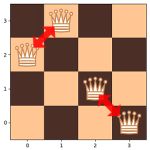
这意味着，在评估以这种方式表示的解时，只需要查找并计算它们代表的位置之间的共享对角线。

问题的表示

为了封装N-Queens问题，创建名为NQueensProblem的Python类。用所需的问题大小初始化该类，并提供以下公共方法：

1. getViolationsCount(positions)：计算给定解违反约束的次数
2. plotBoard(positions)：根据给定的解在棋盘上绘制皇后

棋子图片

# 导入必要库
import numpy as np
import matplotlib as mpl
from matplotlib import pyplot as plt

class NQueensProblem:
    """N皇后问题定义
    """

    def __init__(self,numOfQueens):
        self.numOfQueens = numOfQueens
    
    def __len__(self):
        """
        :return: the number of queens
        """
        return self.numOfQueens
    
    def getViolationsCount(self,positions):
        """
        计算给定解中的违规次数
        由于输入的每一行都包含唯一的列索引，因此行或列不可能违反约束，仅对角线需要计算违反约束数。
        """
        if len(positions) != self.numOfQueens:
            raise ValueError("size of positions list should be equal to ", self.numOfQueens)

        violations = 0

        # 遍历每对皇后，计算它们是否在同一对角线上:
        for i in range(len(positions)):
            for j in range(i + 1, len(positions)):
                #first queen in pair
                column1 = i
                row1 = positions[i]

                #second queen in pair
                column2 = j
                row2 = positions[j]

                if abs(column1 - column2) == abs(row1 - row2):
                    violations += 1
        
        return violations
    
    def plotBoard(self,positions):
        """
        根据给定的解在棋盘上绘制皇后的位置
        """

        if len(positions) != self.numOfQueens:
            raise ValueError("size of positions list must be equal to ",self.numOfQueens)

        fig,ax = plt.subplots()

        #棋盘定义:
        board = np.zeros((self.numOfQueens,self.numOfQueens))
        #棋盘颜色交替
        board[::2,1::2] = 1
        board[1::2,::2] = 1

        #绘制棋盘
        ax.imshow(board,interpolation='none',cmap=mpl.colors.ListedColormap(['#ffc794','#4c2f27']))

        #读取棋子图片，并进行缩放
        queenThumbnail = plt.imread("queen-thumbnail.png")
        thumbnailSpread = 0.70 * np.array([-1,1,-1,1]) / 2

        # 棋子绘制
        for i,j in enumerate(positions):
            #将棋子放在棋盘上
            ax.imshow(queenThumbnail,extent=[j,j,i,i]+thumbnailSpread)
        
        #坐标轴设定
        ax.set(xticks=list(range(self.numOfQueens)),yticks=list(range(self.numOfQueens)))

        ax.axis('image')

        return plt

遗传算法解决N皇后问题

常量及遗传算子定义

1. 导入所需库

from deap import base
from deap import creator
from deap import tools
from deap import algorithms

import random
import array

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

2. 常量定义

# 16皇后
NUM_OF_QUEENS = 16
# 种群中个体数量
POPULATION_SIZE = 300
# 最大代际数
MAX_GENERATIONS = 100
# 交叉概率
P_CROSSOVER = 0.9
#　突变概率
P_MUTATION = 0.1

3. 首先使用要解决的问题的大小创建NQueensProblem类的实例：

nQueens = NQueensProblem(NUM_OF_QUEENS)

4. 由于目标是最大程度地减少违规次数（期望值为0），因此定义最小化适用度策略：

creator.create("FitnessMin",base.Fitness,weights=(-1.0,))

5. 定义个体类

creator.create("Individual",array.array,typecode='i',fitness=creator.FitnessMin)

6. 由于解由有序的整数列表表示，每个整数表示皇后的列位置，因此使用以下定义来创建初始种群：

toolbox = base.Toolbox()
toolbox.register("randomOrder",random.sample,range(len(nQueens)),len(nQueens))

toolbox.register("individualCreator",tools.initIterate,creator.Individual,toolbox.randomOrder)
toolbox.register("populationCreator",tools.initRepeat,list,toolbox.individualCreator)

7. 设置适应度函数以计算皇后在棋盘上的放置所引起的违规次数：

def getViolationCount(individual):
    return nQueens.getViolationsCount(individual),

toolbox.register("evaluate",getViolationCount)

8. 定义遗传算子

toolbox.register("select",tools.selTournament,tournsize=2)
toolbox.register("mate",tools.cxUniformPartialyMatched,indpb=2.0/len(nQueens))
toolbox.register("mutate",tools.mutShuffleIndexes,indpb=1.0/len(nQueens))

使用精英主义策略

使用名人堂可以用来保留进化过程中种群中曾经存在的最佳个体，并不会由于选择，交叉或变异而失去了它们，HallOfFame类在tools模块中实现。
将Halloffame对象用于实现精英主义。 Halloffame对象中包含的个体被直接注入下一代，并且不受选择，交叉和突变的遗传算子的影响

# 名人堂成员数量
HALL_OF_FAME_SIZE = 30
def eaSimpleWithElitism(population,
			toolbox,
            cxpb,
            mutpb,
            ngen,
            stats=None,
            halloffame=None,
            verbose=__debug__):
    """使用halloffame来实现精英机制。 包含在名人堂麦中的个体被直接注入下一代，并且不受选择，交叉和突变的遗传算子的影响。
    """
    
    logbook = tools.Logbook()#用于监控算法运行，和统计数据
    logbook.header = ['gen','nevals'] + (stats.fields if stats else [])

    # 计算个体适应度
    invalid_ind = [ind for ind in population if not ind.fitness.valid]
    fitnesses = toolbox.map(toolbox.evaluate,invalid_ind)
    for ind,fit in zip(invalid_ind,fitnesses):
        ind.fitness.values = fit
    
    if halloffame is None:
        raise ValueError("halloffame parameter must not be empty!")
	#更新名人堂成员
    halloffame.update(population)
    hof_size = len(halloffame.items) if halloffame.items else 0

    record = stats.compile(population) if stats else {
     }
    logbook.record(gen=0,nevals=len(invalid_ind),**record)
    if verbose:
        print(logbook.stream)
    
    #开始遗传流程
    for gen in range(1,ngen + 1):
        #选择个体数目=种群个体数-名人堂成员数
        offspring = toolbox.select(population,len(population) - hof_size)

        #种群更新到下一代
        offspring = algorithms.varAnd(offspring,toolbox,cxpb,mutpb)

        #计算个体适应度
        invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
        fitnesses = toolbox.map(toolbox.evaluate,invalid_ind)
        for ind,fit in zip(invalid_ind,fitnesses):
            ind.fitness.values = fit
        
        #将名人堂成员添加到当前代
        offspring.extend(halloffame.items)

        #更新名人堂
        halloffame.update(offspring)

        #使用当前代替换种群
        population[:] = offspring

        #将当前统计信息附加到日志
        record = stats.compile(population) if stats else {
     }
        logbook.record(gen=gen,nevals=len(invalid_ind),**record)
        if verbose:
            print(logbook.stream)
        
    return population,logbook

遗传流程

使用main函数完成遗传流程

def main():
    #创建初始种群
    population = toolbox.populationCreator(n=POPULATION_SIZE)

    #注册要监听的统计对象
    stats = tools.Statistics(lambda ind: ind.fitness.values)
    stats.register("min",np.min)
    stats.register("avg",np.mean)

    #实例化名人堂对象
    hof = tools.HallOfFame(HALL_OF_FAME_SIZE)

    #运行遗传算法
    population,logbook = eaSimpleWithElitism(population,
            toolbox,
            cxpb=P_CROSSOVER,
            mutpb=P_MUTATION,
            ngen=MAX_GENERATIONS,
            stats=stats,
            halloffame=hof,
            verbose=True)
    
    #打印名人堂成员
    print("- Best solutions are:")
    for i in range(HALL_OF_FAME_SIZE):
        print(i,": ",hof.items[i].fitness.values[0]," -> ",hof.items[i])
    
    #绘制统计结果
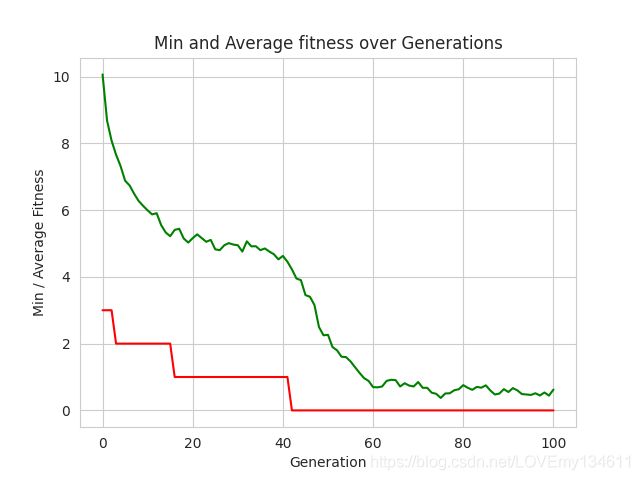
    minFitnessValues,meanFitnessValues = logbook.select("min","avg")
    plt.figure(1)
    sns.set_style("whitegrid")
    plt.plot(minFitnessValues,color='red')
    plt.plot(meanFitnessValues,color='green')
    plt.xlabel('Generation')
    plt.ylabel('Min / Average Fitness')
    plt.title('Min and Average fitness over Generations')

    # 绘制最佳解
    sns.set_style("whitegrid", {
     'axes.grid' : False})
    nQueens.plotBoard(hof.items[0])

    # 绘制结果显示
    plt.show()

结果

运行

if __name__ == "__main__":
    main()

可以看到打印的名人堂成员：

- Best solutions are:
0 :  0.0  ->  Individual('i', [12, 9, 3, 1, 13, 11, 5, 14, 0, 6, 10, 7, 2, 15, 8, 4])
1 :  0.0  ->  Individual('i', [10, 12, 1, 9, 2, 6, 8, 15, 11, 0, 14, 7, 4, 13, 3, 5])
2 :  0.0  ->  Individual('i', [10, 12, 1, 9, 2, 6, 8, 14, 11, 0, 15, 7, 4, 13, 3, 5])
3 :  0.0  ->  Individual('i', [1, 12, 10, 7, 2, 0, 5, 14, 11, 6, 15, 13, 4, 9, 3, 8])
...
29 :  1.0  ->  Individual('i', [9, 14, 4, 10, 12, 0, 5, 1, 11, 15, 2, 7, 8, 13, 3, 6])

绘制最佳解：

最小适应度和平均适应度变化情况：