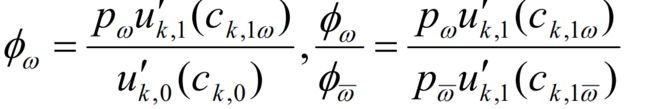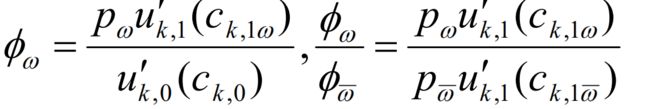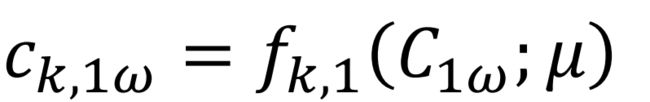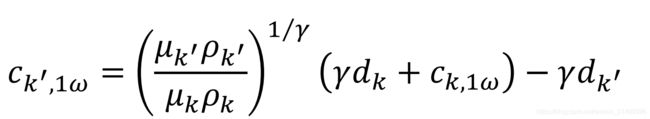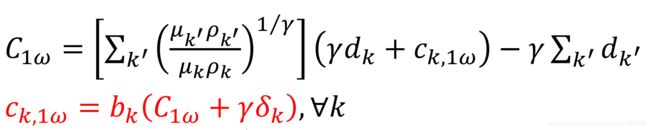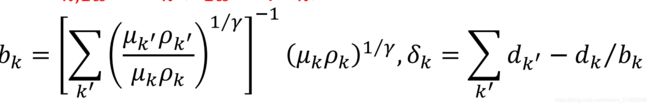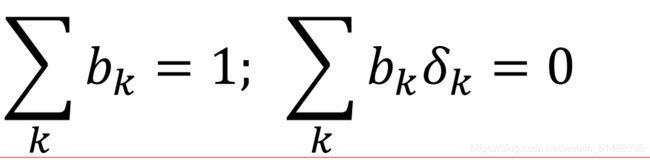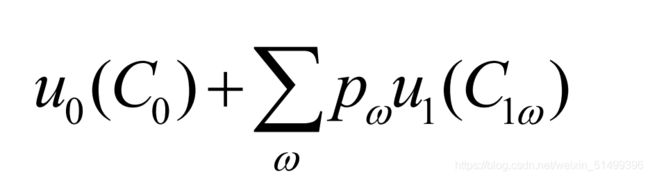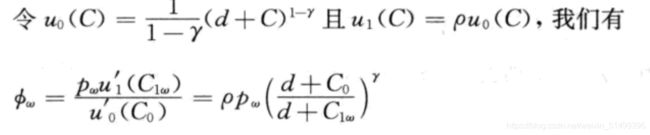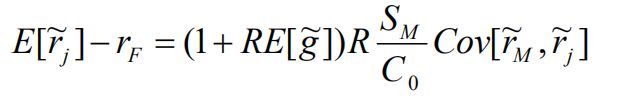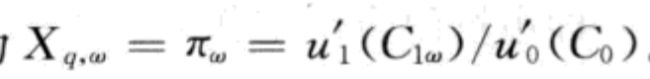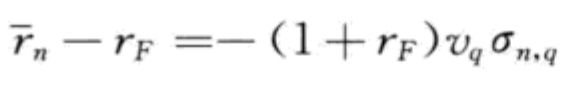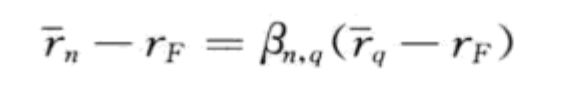金融经济学(王江)期末梳理第十章 完全市场中的资源配置与资产价格 C-CAPM
完全市场中的资源配置
- Introduction
- 10.1 完全市场中的均衡
-
- 10.1.1知识回顾:**完全市场等价于AD市场**
- 10.1.2 参与者各自优化
- 10.1.3 市场出清
- 10.1.4 帕累托最优:引入中央计划者
-
- 1、一阶条件:拉格朗日乘数法
- 2、均衡解的特点:
-
- (1)状态价格
- (2)资源配置
- (3)结论
- 3、最优分享规则(风险/消费):资源配置意味着风险分担
- 4、线性分享规则:最优分享规则的具体形式
- 10.2 代表性参与者
-
- 1、代表性参与者的定义
- 2、构建代表性参与者
-
- 代表性参与者效用函数特征
- 开始构建代表性参与者
- 3、代表性参与者下的均衡求解
-
- 优化问题:
- 一阶条件
- 市场出清: c=C
- 如果代表性参与者的效用函数直接给定 例10.2
- 4、加总:代表性参与者和个体参与者效用函数相同
-
- (1)定义:
- (2)应用
- 10.3 基于消费的资产定价模型(C-CAPM)
-
- 10.3.1 基于消费相对边际效用的定价公式:**最原始的C-CAPM**
-
- 1、根据完全市场均衡价格可以得到原始证券的价格
- 2、用代表性参与者的相对边际效用来表示
- 3、应用
-
- (1)无风险证券定价:
- (2)风险证券n定价:
- 4、具体分析 相关关系Cov( π ~ , X ~ n \tilde\pi,\tilde X_n π~,X~n)
- 10.3.2 C-CAPM的收益率形式
-
- 1、总收益率表示欧拉方程:
- 10.3.3 近似推导CAPM
-
- 1、实利率理论:无风险收益率
- 2、风险资产收益率
-
- (1)应用利率理论
- (2)变形整理CCAPM
- (3)用市场组合收益率替代消费增长率
-
- a、市场组合收益率与消费增长率关系
- b、近似推导CAPM
- c、严格的推导CAPM
Introduction
从第二章建立一般均衡分析基本框架,第三章分析AD市场中的投资组合选择,到期望效用函数的引入,再到第八章对资产组合的排序,第九章根据两基金分离定理,将排序结论应用到多资产组合中,我们得到了资产组合选择的基础理论:如何比较两个组合的好坏:期望收益率和风险。
这一章在三六七八九章的基础上以讨论完全市场中的证券价格和资源配置(取决于组合选择)即求解一般均衡。
1、资源配置 2、个体风险消除 3、共同风险 4、资产价格 5、代表性参与者
6、C-CAPM
10.1 完全市场中的均衡
10.1.1知识回顾:完全市场等价于AD市场
1、由资产定价基本定理:在完全市场中存在唯一的 ϕ \phi ϕ使得 S= ϕ T X \phi^TX ϕTX.
2、这样就可以构造或有状态组合即X θ \theta θ= 1 w 1_w 1w推出 θ w = X − \theta_w=X^- θw=X− 1 ^1 1 1 w 1_w 1w并且这样的组合有Ω个。完全市场中的任意组合都可以表示成或有状态组合的组合。
3、同样每个参与者的0/1期消费和禀赋也可以由状态价格折现到0期,相当于或有状态组合的组合,这等价于AD市场中的预算约束。
4、所以我们使用或有状态组合来表示消费禀赋和组合选择而非原始证券。
5、1期只有交易证券,赋予参与者市场价值等价于赋予其相同的财富(市场化)。
6、思路:参与者各自最优(预算约束)、市场出清(所有参与者加总)、帕累托最优(均衡存在且唯一)、状态价格、证券价格
10.1.2 参与者各自优化
**定理1:**当市场完全时,均衡配置与状态价格和具有相同财富分布的AD经济中一样,而与实际的市场结构以及参与者的禀赋在时间和状态上的分布无关。
证明:引入期望效用函数后,我们只是在第八章分析了基于收益率的一阶条件并未对基于消费的资产配置进行求解。
(1)期望效用函数下的优化问题:
定理2 如果参与者具有严格递增且凹的效用函数,当且仅当 ϕ w p w \phi_w\over p_w pwϕw > ϕ b p b \phi_b\over p_b pbϕb时, c k , c_k, ck, w _w w< c k , c_k, ck, b _b b.
有一阶条件可知 ϕ w p w \phi_w\over p_w pwϕw / ϕ b p b \phi_b\over p_b pbϕb = m u ( c k , mu(c_k, mu(ck, w ) _w) w)/ m u ( c k , mu(c_k, mu(ck, b ) _b) b) 其中 ϕ w p w \phi_w\over p_w pwϕw 叫做状态价格密度(概率重整后的状态价格)
也就是说,状态价格密度之比等于边际效用之比,当某个状态状态价格密度大时,边际效用也大,因此消费就会减少。通俗理解就是价格比较贵。
10.1.3 市场出清
1、证券市场出清:总需求等于总供给等于市场组合。市场组合(风险资产的组合,对于每个参与者每个风险证券的市值占总风险证券的市值一致,所有参与者假加总就是总市值)
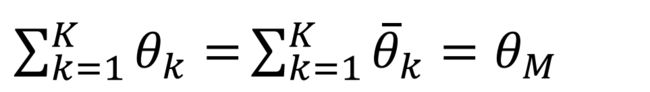
其中 θ k \theta_k θk表示0期对证券的需求即1期的消费也是需求数量
θ ‾ k \overline \theta_k θk表示初始持有的证券即1期禀赋数量
2、对上式两边同时左乘支付矩阵即可得到商品市场出清的条件:

3、有预算约束可以推导0期商品市场出清:

4、结论:完全市场中,证券市场出清意味着商品市场出清(消费禀赋可市场化)
5、例10.1给出了求解均衡的一个例子,得出了资源配置和状态价格。
10.1.4 帕累托最优:引入中央计划者
完全市场得到的均衡时帕累托最优的,AD经济(证明),那么一般情况下,如何判断某一配置是帕累托最优呢?即追求总体最优
1、定理3:配置{ c k c_k ck}是帕累托最优的:
如果存在一组权重 μ k μ_k μk>0(k=1,…K),使得{ c k c_k ck}是中央计划者问题的解:

所谓中央计划者是指面临经济总资源约束的问题,是对所有参与者的效用函数加权平均进行优化,消费受到总消费的约束 将所有参与者联系起来,而完全市场参与者是各自独立的。
1、一阶条件:拉格朗日乘数法
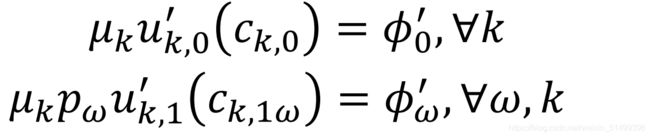
其中 ϕ 1 \phi^1 ϕ1为拉格朗日乘子,所以一阶条件即为帕累托最优的充要条件
所有参与者的相对边际效用,相对于0期,相等,等于拉格朗日乘子的比。
2、均衡解的特点:
(1)状态价格
中央计划者参与者各自最优: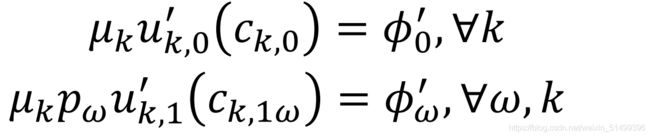
显然如果令状态价格 ϕ w = ϕ w ′ / ϕ 0 ′ \phi_w=\phi'_w/\phi'_0 ϕw=ϕw′/ϕ0′
(2)资源配置
完全市场中参与者各自最优:
![]()
中央计划者参与者各自最优:

参与者各自的资源配置是反解出来的。
显然,如果令 λ k = ϕ ′ / μ k λ_k=\phi'/μ_k λk=ϕ′/μk,资源配置等价于完全市场中的解
(3)结论
令状态价格 ϕ w = ϕ w ′ / ϕ 0 ′ \phi_w=\phi'_w/\phi'_0 ϕw=ϕw′/ϕ0′, λ k = ϕ ′ / μ k λ_k=\phi'/μ_k λk=ϕ′/μk 中央计划者问题均衡等价于完全市场均衡。即任意一个帕累托最优配置,都可以由完全证券市场下,相对于财富C在参与者之间的某个配置的市场均衡来达到。(福利经济学第二定理)
3、最优分享规则(风险/消费):资源配置意味着风险分担
(1)由中央计划者均衡解及总资源约束:在每个状态有

(2)只看第一个因式和第三个因式,得到拉格朗日乘子是关于总资源和权重向量的函数即(其中概率分布应该给定虽然不同,但也是个常数)与状态有关。如果是C则与状态无关。
性质2 总资源越多,消费越多。

(1)对于每个参与者相同状态下的拉格朗日乘子是相同的:
一个状态对于一个拉格朗日乘子(每个状态也对应一个消费)、状态空间概率分布相同。
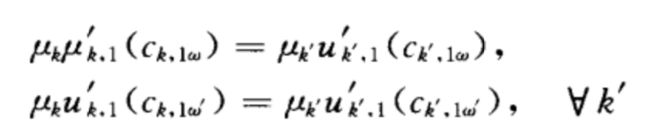
(2)所以,如果对于某个k有 c w < c b c_w
(3)如果是完全市场:是上述中央计划者的一个解,无权重向量,那么消费只与总禀赋有关,即 c k = f ( C ) c_k=f(C) ck=f(C),总禀赋越高,消费越高,同时他们也承担了相应消费带来的风险,他们的风险与他们自身的禀赋无关,在证券市场上的交易使得他们消除了与总禀赋风险无关的风险即非系统风险。因此在完全市场中,风险分担是最优的。
(4)对资产定价的意义:给定参与者的财富分布,证券价格只与总体风险有关而与个体风险μ无关。
4、线性分享规则:最优分享规则的具体形式
线性分享规则即c是C的线性函数,有如下定理:

证明:
(1)识别效用函数:HARA双曲线且具有相同的指数γ
我们看到形式如同stiglitz两基金分离定理的效用函数,我们知道这种效用函数,两基金分离成立(证明将其写成权重收益的效用函数)
(2)一阶条件:

(3)将给定效用函数带入得到:
所以分享规则是线性的。
10.2 代表性参与者
上一节得到了,完全市场的资源配置和均衡价格,并且引入中央计划者问题分析了帕累托最优配置,这一节将中央计划者问题看作时间可分离的,分别求解0期和1期代表性参与者的最优条件。
1、代表性参与者的定义
首先,将中央计划者问题分解为:两个子问题
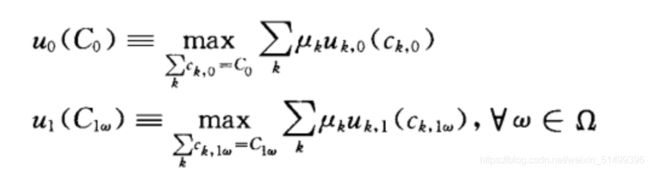
那么,代表性参与者的期望效用函数可定义为:代表了整个经济
2、构建代表性参与者
给定单个参与者的效用函数,如何构建代表性参与者的效用函数呢?可以看到代表性参与者的效用函数是每个参与者的效用函数的加权,那么两者应该具有相同的形式,通过变量代换即可进行构造,下面先介绍一个定理。
代表性参与者效用函数特征
如果所有参与者都具有递增且严格凹性的效用函数,那么代表性参与者的效用函数也是递增和严格凹性的。
证明:
(1)先证明一阶导大于0
对代表性参与者效应函数求导:
0期: u 0 ′ ( C 0 ) = ∑ k μ k u k ′ ( c k u_0'(C_0)=\sum_k μ_ku_k'(c_k u0′(C0)=∑kμkuk′(ck_0 ) f ′ ( C 0 ) )f'(C_0) )f′(C0) 其中c是C的函数。
由中央计划者最优条件: μ k u k ′ ( c k μ_ku_k'(c_k μkuk′(ck_0) = ϕ 0 ′ \phi_0' ϕ0′ 对所有参与者成立
因此 u 0 ′ ( C 0 ) = ϕ 0 ′ ∑ k f ′ ( C 0 ) u_0'(C_0)=\phi_0'\sum_k f'(C_0) u0′(C0)=ϕ0′∑kf′(C0) 显然求和部分等于1(前面结论)
所以 u 0 ′ ( C 0 ) = ϕ 0 ′ u_0'(C_0)=\phi_0' u0′(C0)=ϕ0′
对于1期的某个状态,显然也有同样的结论
u 1 ′ ( C w ) = ∑ k μ k u k ′ ( c k u_1'(C_w)=\sum_k μ_ku_k'(c_k u1′(Cw)=∑kμkuk′(ck_w ) f ′ ( C w ) )f'(C_w) )f′(Cw)
由中央计划者最优条件: μ k u k ′ ( c k μ_ku_k'(c_k μkuk′(ck_w) = ϕ w ′ \phi_w' ϕw′
u 1 ′ ( C w ) = ϕ w ′ ∑ k f ′ ( C w ) u_1'(C_w)=\phi_w'\sum_k f'(C_w) u1′(Cw)=ϕw′∑kf′(Cw)
因此 u 1 ′ ( C w ) = ϕ w ′ u_1'(C_w)=\phi_w' u1′(Cw)=ϕw′
由KKT条件可知 u 0 ′ ( C 0 ) = ϕ 0 ′ > 0 u_0'(C_0)=\phi_0'>0 u0′(C0)=ϕ0′>0, u 1 ′ ( C w ) = ϕ w ′ > 0 u_1'(C_w)=\phi_w'>0 u1′(Cw)=ϕw′>0
(2)二阶导小于0

显然,由于参与者效用函数二阶导小于0,代表性参与者效用函数二阶导也小于0
开始构建代表性参与者
由前面定理证明我们知道 u 0 ′ ( C 0 ) = ϕ 0 ′ > 0 u_0'(C_0)=\phi_0'>0 u0′(C0)=ϕ0′>0, u 1 ′ ( C w ) = ϕ w ′ > 0 u_1'(C_w)=\phi_w'>0 u1′(Cw)=ϕw′>0
而参与者各自优化一阶条件为:
μ k u k ′ ( c k μ_ku_k'(c_k μkuk′(ck_0) = ϕ 0 ′ \phi_0' ϕ0′
μ k u k ′ ( c k μ_ku_k'(c_k μkuk′(ck_w) = ϕ w ′ \phi_w' ϕw′
所以
u 0 ′ ( C 0 ) = ϕ 0 ′ u_0'(C_0)=\phi_0' u0′(C0)=ϕ0′= μ k u k ′ ( c k μ_ku_k'(c_k μkuk′(ck_0)
u 1 ′ ( C w ) = ϕ w ′ u_1'(C_w)=\phi_w' u1′(Cw)=ϕw′= μ k u k ′ ( c k μ_ku_k'(c_k μkuk′(ck_w)
因为我们已知参与者的效用函数,将其一阶导带入(当然这里均衡已经求解过)即可,其中c是C的函数,所以得到了代表性参与者的效用函数。
3、代表性参与者下的均衡求解
假设市场中只有代表性参与者的情形:
优化问题:
一阶条件
市场出清: c=C
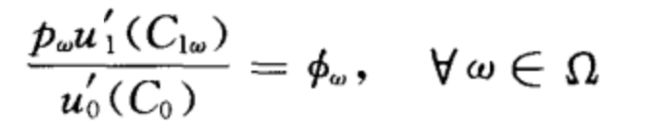
其中 ϕ w \phi_w ϕw为状态价格,可以看到与完全市场中的参与者均衡等价。消费就是禀赋,状态价格就是相对边际效用。
所以这个只有代表性参与者的市场等价于所有参与者的完全市场,我们称代表性参与者代表了整个完全市场。
如果我们的目的是为了资产定价即寻求状态价格,那么只需要知道如何构建代表性参与者的效用函数和经济中的总禀赋就可以求得状态价格。
如果代表性参与者的效用函数直接给定 例10.2
4、加总:代表性参与者和个体参与者效用函数相同
(1)定义:
代表性参与者的效用函数是由两个最优化问题定义的,那么不管0期还是1期的效用函数都取决与参与者效用函数和预算约束即财富分布。所以即使所有参与者效用函数相同,代表性参与者的效用函数也有可能是其他形式。但是确实存在代表性参与者和个体参与者效用函数形式相同的情况,这种情况称作存在(简单的)加总或聚集。
(2)应用
定理:如果参与者都具有相同的效用函数形式: 其中只有d不同。
那么代表性参与者具有与个体参与者相同形式的效用函数:
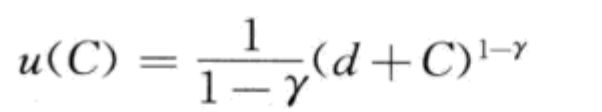
识别:幂指数形式的效用函数,值得一提的是对数效用函数可以看作特殊的幂指形的效用函数,γ趋于1的极限效用。
所以对于对数效用和幂指数效用不用求解均衡即可计算均衡状态价格。
10.3 基于消费的资产定价模型(C-CAPM)
前面分析了完全市场的均衡(资源配置和状态价格),这一节进一步分析资产的均衡价格和经济基本面的关系(基于组合选择部分)如期望收益率和经济的总体风险和总体的风险厌恶程度。
10.3.1 基于消费相对边际效用的定价公式:最原始的C-CAPM
1、根据完全市场均衡价格可以得到原始证券的价格
2、用代表性参与者的相对边际效用来表示

可以看到,价格由状态价格向量对支付的折现转化为相对边际效用对支付的折现。
3、应用
(1)无风险证券定价:
B= 1 1 + r F 1\over1+r_F 1+rF1 = E[ π ~ \tilde{\pi} π~]
(2)风险证券n定价:
S n = E [ π ~ ] S_n=E[\tilde\pi] Sn=E[π~] E [ X ~ n ] E[\tilde X_n] E[X~n] + Cov[ π ~ , X ~ n \tilde\pi,\tilde X_n π~,X~n] = E[ X ~ n \tilde X_n X~n]/( 1 + r F 1+r_F 1+rF)+ Cov[ π ~ , X ~ n \tilde\pi,\tilde X_n π~,X~n]
如果没有风险,那么证券价格就是其支付以无风险利率贴现,而第二项表示风险带来的价格变化。所以资产价格不仅却取决于该证券未来的支付,还取决于整个经济中代表性参与者的相对边际效用,而这个相对边际效用 π ~ \tilde\pi π~取决于代表性参与者的总禀赋的分布(在给定代表性参与者效用函数的情况下)。
如果某项资产的未来支付和总禀赋无关,那么价格就是支付的贴现
如果某项资产的未来支付和总禀赋相关,那么价格就是支付的贴现+总体风险
个体风险为与代表性参与者相对边际效用无关的部分。
4、具体分析 相关关系Cov( π ~ , X ~ n \tilde\pi,\tilde X_n π~,X~n)
关键词 :高支付 => 相对边际效用 =>资源(这里边际效用与总禀赋相关)
(1)负相关:基于1期相对于0期分析
意味着低相对边际效用,但是支付却很高,因为边际效用递减规律,所以低相对边际效用对应需要高消费。因此在资源丰富,额外消费价值相对较低时,支付较高,资源稀缺,额外消费价值相对较高时,支付较低,这显然是我们所不希望看到的,所以价格中相应的风险调整项是负的。折价的大小取决于协方差大小的绝对值。也就是说协方差越大,证券风险越大(与总禀赋相关性强),折价也越大
(2)正相关:保险(发生事故,资源稀缺,需要钱,越多钱,保险费越多)
意味着低相对边际效用,低支付;高相对边际效用,高支付。因此这只证券在资源相对稀缺,额外消费价值相对较高时(边际效用递减规律),支付较高,这正是我们所希望的。所以有溢价,溢价大小取决于协方差的大小,就是说协方差越大,证券风险越大(与总禀赋相关性强),溢价也越大。
10.3.2 C-CAPM的收益率形式
1、总收益率表示欧拉方程:
(1)E[ π ~ x ~ n \tilde\pi \tilde x_n π~x~n]=1,E[ π ~ x F \tilde\pi x_F π~xF]=1,
( 。 ~ \tilde。 。~)表示不确定性xf为确定性的。
所以E[ π ~ ( x ~ n − x F ) \tilde\pi( \tilde x_n-x_F) π~(x~n−xF)]=0 E[ π ~ ( r ~ n − r F ) \tilde\pi( \tilde r_n-r_F) π~(r~n−rF)]=0
乘积的期望等于期望的乘积+协方差
(2)通过一系列整理可以得到收益率形式的CCAPM
E[ π ~ ] \tilde\pi] π~]= 1 / 1 + r F 1/1+r_F 1/1+rF
(E[ r ~ n \tilde r_n r~n]- r F r_F rF) *1/ ( 1 + r F ) (1+r_F) (1+rF)+Cov( π ~ , r ~ n − r F \tilde\pi,\tilde r_n-r_F π~,r~n−rF)=0
(E[ r ~ n \tilde r_n r~n]- r F r_F rF) *1/ ( 1 + r F ) (1+r_F) (1+rF)+Cov( π ~ , r ~ n \tilde\pi,\tilde r_n π~,r~n)=0
E[ r ~ n \tilde r_n r~n]= r F r_F rF- ( 1 + r F ) (1+r_F) (1+rF)Cov( π ~ , r ~ n \tilde\pi,\tilde r_n π~,r~n)
所以风险溢价与协方差(收益率和相对边际效用)负相关,当协方差为正时,溢价为负,协方差为负时,溢价为正。
证券n的期望收益率 r ‾ = \overline r= r=E[ r ~ n \tilde r_n r~n]= r F r_F rF- ( 1 + r F ) (1+r_F) (1+rF)Cov( π ~ , r ~ n \tilde\pi,\tilde r_n π~,r~n)
那么可以得到现值公式: S n = S_n= Sn= E [ X ~ ] 1 + r ‾ n E[\tilde X]\over1+\overline r_n 1+rnE[X~]
表示证券价格是证券的期望支付对一个风险调整后的折现率折现
10.3.3 近似推导CAPM
1、实利率理论:无风险收益率
设定 g ~ \tilde g g~为消费增长率且取值范围很小,那么 C ~ 1 = ( 1 + g ~ ) C 0 \tilde C_1=(1+ \tilde g)C_0 C~1=(1+g~)C0,
那么相对边际效用 π ~ \tilde \pi π~=ρ u ′ ( C ~ 1 ) u ′ ( C ~ 0 ) u'(\tilde C_1)\over u'(\tilde C_0) u′(C~0)u′(C~1)
其中 u ′ ( C ~ 1 ) = u ′ ( C 0 + C 0 g ~ ) = u ′ ( C 0 ) + u ′ ′ ( C 0 ) C 0 g ~ + o ( g ~ ) u'(\tilde C_1)=u'(C_0+C_0\tilde g)=u'(C_0)+u''(C_0)C_0\tilde g+o(\tilde g) u′(C~1)=u′(C0+C0g~)=u′(C0)+u′′(C0)C0g~+o(g~)
那么相对边际效用
π ~ \tilde \pi π~=ρ u ′ ( C 0 ) + u ′ ′ ( C 0 ) C 0 g ~ + o ( g ~ ) u ′ ( C ~ 0 ) u'(C_0)+u''(C_0)C_0\tilde g+o(\tilde g)\over u'(\tilde C_0) u′(C~0)u′(C0)+u′′(C0)C0g~+o(g~)=ρ[1-( − u ′ ′ ( C 0 ) C 0 u ′ ( C ~ 0 ) -u''(C_0)C_0\over u'(\tilde C_0) u′(C~0)−u′′(C0)C0) g ~ + o ( g ~ ) \tilde g+o(\tilde g) g~+o(g~)]
可以看到圆括号里为相对风险厌恶系数记作R,同时R也反映了边际效用对C的依赖。忽略高阶项有
E [ π ~ ] ≈ ρ [ 1 − R E [ g ~ ] ] = ρ [ 1 − R g ‾ ] ] E[\tilde \pi]\approx ρ[1-RE[\tilde g]]=ρ[1-R\overline g]] E[π~]≈ρ[1−RE[g~]]=ρ[1−Rg]]
1/ ( 1 + r F ) = E [ π ~ ] ≈ ρ [ 1 − R g ‾ ] ] (1+r_F)=E[\tilde \pi]\approxρ[1-R\overline g]] (1+rF)=E[π~]≈ρ[1−Rg]]
r F ≈ r_F \approx rF≈( 1 ρ 1\overρ ρ1-1)+ R ρ R\overρ ρR g ‾ \overline g g
利率与预期消费增长率成正比,消费增长时,储蓄少,资金供给少,银行利率会增加。利率与时间偏好系数成反比,时间偏好系数越大,越看重未来消费,这样就会减少当前消费,增加储蓄,储蓄多了,利率自然下降。
2、风险资产收益率
r ‾ = \overline r= r=E[ r ~ n \tilde r_n r~n]= r F r_F rF- ( 1 + r F ) (1+r_F) (1+rF)Cov( π ~ , r ~ n \tilde\pi,\tilde r_n π~,r~n)
(1)应用利率理论
将 r F ≈ r_F \approx rF≈( 1 ρ 1\overρ ρ1-1)+ R ρ R\overρ ρR g ‾ \overline g g带入
r ‾ n − r F ≈ \overline r_n-r_F \approx rn−rF≈- 1 ρ 1\over ρ ρ1 ( 1 + R g ‾ ) (1+R\overline g) (1+Rg)Cov( π ~ , r ~ n \tilde\pi,\tilde r_n π~,r~n)
(2)变形整理CCAPM
π ~ ≈ ρ [ 1 − R g ~ ] \tilde \pi\approx ρ[1-R\tilde g] π~≈ρ[1−Rg~]
C o v ( π ~ , r ~ n ) = C o v ( ρ [ 1 − R g ~ ] , r ~ n ) = − ρ R C o v ( g ~ , r ~ n ) Cov(\tilde\pi,\tilde r_n)=Cov(ρ[1-R\tilde g],\tilde r_n)=-ρRCov(\tilde g,\tilde r_n) Cov(π~,r~n)=Cov(ρ[1−Rg~],r~n)=−ρRCov(g~,r~n)
r ‾ n − r F ≈ \overline r_n-r_F \approx rn−rF≈ - 1 ρ 1\over ρ ρ1 ( 1 + R g ‾ ) (1+R\overline g) (1+Rg)Cov( π ~ , r ~ n \tilde\pi,\tilde r_n π~,r~n) ≈ ( 1 + R g ‾ ) R C o v ( g ~ , r ~ n ) \approx(1+R\overline g)RCov(\tilde g,\tilde r_n) ≈(1+Rg)RCov(g~,r~n)
我们进一步探讨上式的意义:需要对其进行简化
(3)用市场组合收益率替代消费增长率
a、市场组合收益率与消费增长率关系
假设1期所有可交易证券构成一个组合即市场组合m,那么m的总支付即为经济中的总禀赋和总消费。由于市场是完全的,所以可由AD证券来描述市场组合即 θ m = C 1 θ_m=C_1 θm=C1即可通过AD证券复制消费,组合就是消费。组合现值为 S m = ϕ T C 1 S_m=\phi^TC_1 Sm=ϕTC1
则收益率为:
所以 r ‾ n − r F ≈ \overline r_n-r_F \approx rn−rF≈ - 1 ρ 1\over ρ ρ1 ( 1 + R g ‾ ) (1+R\overline g) (1+Rg)Cov( π ~ , r ~ n \tilde\pi,\tilde r_n π~,r~n) ≈ ( 1 + R g ‾ ) R C o v ( g ~ , r ~ n ) \approx(1+R\overline g)RCov(\tilde g,\tilde r_n) ≈(1+Rg)RCov(g~,r~n)
b、近似推导CAPM
取j=m ,则有 r ‾ m − r F ≈ \overline r_m-r_F \approx rm−rF≈ ( 1 + R g ‾ ) R (1+R\overline g)R (1+Rg)R S m C 0 S_m\over C_0 C0Sm σ m 2 σ_m^2 σm2
将 ( 1 + R g ‾ ) R (1+R\overline g)R (1+Rg)R S m C 0 S_m\over C_0 C0Sm带入原式有
r ‾ n − r F ≈ β m \overline r_n-r_F \approx β_m rn−rF≈βm , n ( r ‾ m − r F ) ,_n(\overline r_m-r_F) ,n(rm−rF) , 其中 β m β_m βm , n ,_n ,n=Cov( r ~ m , r ~ n ) / σ m 2 \tilde r_m,\tilde r_n )/σ_m^2 r~m,r~n)/σm2
解释:市场组合的收益率的风险是整个经济的总体风险,回归系数β表示,一个资产的收益率所承担的总体风险的部分。它的风险溢价等于该系数乘以总体风险的溢价。这就是著名的资本资产定价模型CAPM.
缺点:这里得到的CAPM是以消费为基础的资本资产定价模型的近似以市场组合的收益来近似 π ~ \tilde \pi π~即相对边际效用。
怎么理解:
在无风险利率理论中我们用 g ~ \tilde g g~来近似相对边际效用,然后再风险收益率中我们又用市场组合收益率来近似 g ~ \tilde g g~。所以只是选择了一个组合来近似代表性参与者的相对边际效用
c、严格的推导CAPM
C-CAPM: r ‾ = \overline r= r=E[ r ~ n \tilde r_n r~n]= r F r_F rF- ( 1 + r F ) (1+r_F) (1+rF)Cov( π ~ , r ~ n \tilde\pi,\tilde r_n π~,r~n)
(1)组合q的支付向量就是相对边际效用: