金融经济学(王江)期末梳理第十二章 μ-σ 分析组合选择
均值方差偏好下的投资组合选择
- Introduction
- 12.1 均值-方差偏好
-
- 12.1.1 均值-方差偏好的定义
- 12.1.2 二次效用函数具有均值方差偏好
-
- 1、证明
- 2、理解
- 12.1.3多元联合正态分布的支付具有均值方差偏好
-
- 1、证明
- 2、解释
- 12.2 均值-方差前沿组合
-
- 12.2.1 一些基本概念
- 12.2 均值-方差前沿组合的求解(MVF)
- 12.2 均值-方差前沿组合的性质 MVF
-
- 12.2.1参与者的最优组合在均值方差前沿上
- 12.2.2 均值方差偏好下两基金分离定理成立
- 12.2.3 均值方差前沿是双曲线的一支
- 12.2.4 最小方差组合 MVP
- 12.2.5 均值方差有效组合MVE
- 12.2.6 均值方差前沿组合和任意组合关系(CAPM)
- 12.3 存在无风险证券时的CAPM
-
- 12.3.1 存在无风险证券时的组合选择:CML
-
- 1、优化问题
- 2、求解
- 3、解的讨论:切点组合
- 12.3.2 几何方法推导两基金分离:CML
-
- 1、风险证券的构建:测度变换
-
- 2、将风险证券和无风险证券组合
- 12.3.3 任意组合的定价公式:
Introduction
第八、九章,我们对收益率分布和效用函数做出一些假设后,得出了如何进行投资选择,第十章在前两章的基础上进一步得出了完全市场下的均衡价格和资源配置,并且说明了这种均衡时帕累托最优的。但是,此时的均衡价格和组合选择依赖于相对边际效用,其取决于未来财富的分布,不具有可操作性。将理论进一步贴近实际,本章选取未来财富的分布两个特征:期望和方差,以期得到更加具体的结论。同前几章一样,我们假定参与者的消费、储蓄决策是给定的,只考虑组合选择问题,同样假定1期禀赋是可以市场化的。
12.1 均值-方差偏好
12.1.1 均值-方差偏好的定义
我们将未来财富的期望效用在财富均值 w ‾ \overline w w点展开:
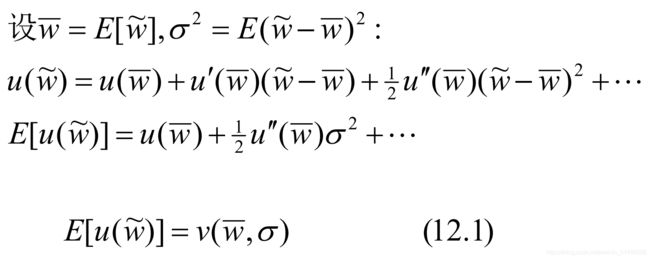
对所有效用函数,我们通过泰勒展开近似地可以将将期望效用函数写成均值和标准差(忽略高阶矩)的间接效用形式,也称作均值方差偏好。但是严格来说上式只有在满足一定条件下才成立,下面给出两个例子
12.1.2 二次效用函数具有均值方差偏好
1、证明
对于一般二次效用函数:u(w)= w- 1 2 1\over2 21 a w 2 aw^2 aw2 有 u ( w ~ ) = v ( w ‾ , σ w ) u(\tilde w)=v(\overline w, σ_w) u(w~)=v(w,σw) 其中a>0.
E [ u ( w ~ ) ] = E w ~ − E[u(\tilde w)] = E\tilde w - E[u(w~)]=Ew~− 1 2 1\over2 21 a E ( w ~ 2 ) aE(\tilde w^2) aE(w~2) = E w ~ E\tilde w Ew~ 1 2 1\over2 21 a [ ( E ( w ~ ) ) 2 + V a r ( w ~ ) ] a[(E(\tilde w))^2+Var(\tilde w)] a[(E(w~))2+Var(w~)] =
( 1 − (1- (1− a 2 a\over2 2a w ‾ ) w ‾ − \overline w)\overline w - w)w− a 2 a\over2 2a σ w 2 σ_w^2 σw2 #
2、理解
对于上面的效用函数,我们希望 v ( w ‾ , σ w ) v(\overline w, σ_w) v(w,σw) 其中a>0.对于 w ‾ \overline w w 递增,对于 σ w σ_w σw递减,也就是说参与者对财富的预期水平 w ‾ \overline w w是喜好的,对于财富的不确定性即 σ w σ_w σw是厌恶的。
从函数形式上也可以看到, v ( w ‾ , σ w ) v(\overline w, σ_w) v(w,σw) 对 w ‾ \overline w w 有不满足性,对 σ w σ_w σw没有不满足性,但是对于两者都具有凹性。
12.1.3多元联合正态分布的支付具有均值方差偏好
1、证明
如果收益分布 X ~ \tilde X X~满足联合正态分布, 有 u ( w ~ ) = v ( w ‾ , σ w ) u(\tilde w)=v(\overline w, σ_w) u(w~)=v(w,σw) .
如果 X ~ \tilde X X~服从正态分布,那么 w ~ = X ~ θ \tilde w=\tilde Xθ w~=X~θ也服从正态分布。定义 e ~ = ( w ~ − w ‾ ) / σ w \tilde e=(\tilde w- \overline w)/σ_w e~=(w~−w)/σw, 那么 e ~ \tilde e e~ 服从标准正态分布。且 w ~ = w ‾ + σ w e ~ \tilde w =\overline w +σ_w \tilde e w~=w+σwe~, 因此 u ( w ~ ) = v ( w ‾ , σ ) u(\tilde w)=v(\overline w, σ) u(w~)=v(w,σ)
2、解释
可以看到,结论和二次效用函数完全一致。
综上所述,(期望效用函数)均值-方差的偏好对均值递增,对方差递减。
12.2 均值-方差前沿组合
12.2.1 一些基本概念
N只收益率线性无关的证券
N只证券的收益率向量 r ~ = [ r ~ 1 ; r ~ 2 ; … ; r ~ N ] \tilde r=[\tilde r_1;\tilde r_2;…;\tilde r_N] r~=[r~1;r~2;…;r~N] 均值向量 r ‾ = r ~ \overline r=\tilde r r=r~
N只证券的收益率的协差阵∑=E [ ( r ~ − r ‾ ) ( r ~ − r ‾ ) T ] [(\tilde r-\overline r)(\tilde r-\overline r)^T] [(r~−r)(r~−r)T], 对称 N*N 假设 r ‾ ≠ 0 \overline r\not=0 r=0
组合z:
N只证券的权重向量:z = [ z 1 ; z 2 ; … ; z N ] [z_1;z_2;…;z_N] [z1;z2;…;zN]
组合z的收益率(数) r ~ z = z T r ~ \tilde r_z=z^T\tilde r r~z=zTr~
组合z的期望收益率(数) r ‾ z = z T r ‾ \overline r_z=z^T\overline r rz=zTr
组合z的期望收益率的方差 σ z 2 = z T ∑ z σ_z^2 =z^T∑z σz2=zT∑z
组合z的期望财富:用w投资给组合z 已知收益率的前提下考虑(以前使用支付矩阵)
则组合z的期望财富为:w(1+ r ‾ z \overline r_z rz)=E [ w ~ ] [\tilde w] [w~]
在财富为w的情况下选择组合z的期望收益的方差:Var( w ~ \tilde w w~)= w 2 σ z 2 w^2σ_z^2 w2σz2= w 2 z T ∑ z w^2z^T∑z w2zT∑z
在具有均值-方差偏好下,我们将只关注组合收益率的均值和方差,这一章都是在给定期望收益率的条件下考虑方差最小(等价于方差给定组合期望收益率最大)
12.2 均值-方差前沿组合的求解(MVF)
Mean-Variance Frontier
考虑下面优化问题:

1、构建拉格朗日函数:(矩阵求导知识1/2为了计算方便:两个等式约束)

2、一阶条件:∑ 正定,保证二阶条件自动满足(?)
∑ z − λ r r ‾ − λ 1 l = 0 ∑z-λ_r\overline r-λ_1l=0 ∑z−λrr−λ1l=0 (1)
r ‾ p − z T r ‾ = 0 \overline r_p-z^T\overline r=0 rp−zTr=0 (2)
1 − z T l = 0 1-z^Tl=0 1−zTl=0 (3)
这个方程组如何解呢?
step1:
首先由(1)有
z= ∑ − ∑^- ∑− 1 ( λ r r ‾ − λ 1 l ) ^1(λ_r\overline r-λ_1l) 1(λrr−λ1l), 要求得组合选择必须解出两个拉格朗日乘数
z T = ( λ r r ‾ T − λ 1 l T ) ∑ − z^T=(λ_r\overline r^T-λ_1l^T)∑^- zT=(λrrT−λ1lT)∑− 1 ^1 1
step2:
分别带入(2)(3)得到
r ‾ p = ( λ r r ‾ T − λ 1 l T ) ∑ − \overline r_p=(λ_r\overline r^T-λ_1l^T)∑^- rp=(λrrT−λ1lT)∑− 1 r ‾ = λ r r ‾ T ∑ − ^1\overline r=λ_r\overline r^T∑^- 1r=λrrT∑− 1 r ‾ − λ 1 l T ∑ − ^1\overline r-λ_1l^T∑^- 1r−λ1lT∑− 1 r ‾ ^1\overline r 1r = λ r b + λ 1 a λ_rb+λ_1a λrb+λ1a(设置两个类似二次型的参数b,a)
1= ( λ r r ‾ T − λ 1 l T ) ∑ − (λ_r\overline r^T-λ_1l^T)∑^- (λrrT−λ1lT)∑− 1 l ^1l 1l= λ r a + λ 1 c λ_ra+λ_1c λra+λ1c(二次型转置相同,设置一个类似二次型的参数c)
其中
b = r ‾ T ∑ − b=\overline r^T∑^- b=rT∑− 1 r ‾ ^1\overline r 1r
a = l T ∑ − a=l^T∑^- a=lT∑− 1 r ‾ ^1\overline r 1r
c = l T ∑ − c=l^T∑^- c=lT∑− 1 l ^1l 1l
step3:
令 d = b c − a 2 d=bc-a^2 d=bc−a2,则由克拉默法则可解下列方程组:
r ‾ p = λ r b + λ 1 a \overline r_p=λ_rb+λ_1a rp=λrb+λ1a
1 = λ r a + λ 1 c 1 =λ_ra+λ_1c 1=λra+λ1c
λ r = λ_r= λr= c r ‾ p − a d c\overline r_p-a\over d dcrp−a λ 1 = λ_1= λ1= b − a r ‾ p d b-a\overline r_p\over d db−arp
step4:带入z的解析式有:

所以对于给定期望收益率,存在唯一的解即组合使得方差最小,每一个期望收益率对应一个方差最小的组合。所有的组合z构成了均值方差前沿,所有最小方差中方差最小的组合即均值方差前沿(MVF)的顶点叫做最小方差组合(MVP)。那么如何形象的表示呢?下一节我们会给出证明:是双曲线
12.2 均值-方差前沿组合的性质 MVF
12.2.1参与者的最优组合在均值方差前沿上
如果具有均值方差偏好的参与者的最优组合不在方差前沿上,那么对于给定的期望收益率,在均值方差前沿上一定存在一个组合比该参与者持有组合的收益率的方差小,根据均值方差偏好对于方差递减,该参与者持有组合就不是最优组合。
12.2.2 均值方差偏好下两基金分离定理成立
(1)我们观察上一节求出的解:

其中 b = r ‾ T ∑ − b=\overline r^T∑^- b=rT∑− 1 r ‾ ^1\overline r 1r , a = l T ∑ − a=l^T∑^- a=lT∑− 1 r ‾ ^1\overline r 1r, c = l T ∑ − c=l^T∑^- c=lT∑− 1 l ^1l 1l
我们知道所有的z构成均值方差前沿组合,所以取 r ‾ p = 0 \overline r_p=0 rp=0使得z= z 0 z_0 z0也是均值方差前沿组合。取 r ‾ p = 1 \overline r_p=1 rp=1使得z= z 1 z_1 z1也是均值方差前沿组合。
(2)首先均值方差前沿组合是 z 0 , z 1 z_0,z_1 z0,z1这两个MVF组合的组合。
(3)这两个MVF组合成另外两个MVF也可以组合成任意均值方差前沿组合。
(4)所以均值方差前沿组合可以由任意两个MVF组合组合而成。
(5)然后参与者的最优组合都是均值方差前沿组合,由 z 0 , z 1 z_0,z_1 z0,z1这两个MVF组合组成,最优组合是位于 R N R^N RN中连接 z 0 , z 1 z_0,z_1 z0,z1直线上的组合,因此两基金分离成立。
12.2.3 均值方差前沿是双曲线的一支
(1)均值方差前沿组合为: z p = z 0 + ( z 1 − z 0 ) r ‾ p z_p=z_0+(z_1-z_0)\overline r_p zp=z0+(z1−z0)rp
那么,均值方差前沿组合收益率为 r ~ p = z p T r ~ \tilde r_p = z_p^T\tilde r r~p=zpTr~
所以,均值方差前沿组合收益率的方差为:
σ p 2 = z p T ∑ z p = [ z 0 + ( z 1 − z 0 ) r ‾ p ] T ∑ [ z 0 + ( z 1 − z 0 ) r ‾ p ] σ_p^2=z_p^T∑z_p=[z_0+(z_1-z_0)\overline r_p]^T∑[z_0+(z_1-z_0)\overline r_p] σp2=zpT∑zp=[z0+(z1−z0)rp]T∑[z0+(z1−z0)rp]
则 σ p = [ z 0 + ( z 1 − z 0 ) r ‾ p ] T ∑ [ z 0 + ( z 1 − z 0 ) r ‾ p ] = z 0 T ∑ z 0 + 2 z 0 T ∑ ( z 1 − z 0 ) r ‾ p + ( z 1 − z 0 ) T ∑ ( z 1 − z 0 ) r ‾ p 2 σ_p=\sqrt {[z_0+(z_1-z_0)\overline r_p]^T∑[z_0+(z_1-z_0)\overline r_p]}= \sqrt{z_0^T∑z_0+2z_0^T∑(z_1-z_0)\overline r_p+(z_1-z_0)^T∑(z_1-z_0)\overline r_p^2} σp=[z0+(z1−z0)rp]T∑[z0+(z1−z0)rp]=z0T∑z0+2z0T∑(z1−z0)rp+(z1−z0)T∑(z1−z0)rp2
即证均值方差前沿是双曲线的一支
12.2.4 最小方差组合 MVP
1、求解MVP的收益率的期望和方差
(1)均值方差前沿顶点为MVP,下面进行求解:使下面式子最小化:
σ p 2 = z 0 T ∑ z 0 + 2 z 0 T ∑ ( z 1 − z 0 ) r ‾ p + ( z 1 − z 0 ) T ∑ ( z 1 − z 0 ) r ‾ p 2 σ_p^2=z_0^T∑z_0+2z_0^T∑(z_1-z_0)\overline r_p+(z_1-z_0)^T∑(z_1-z_0)\overline r_p^2 σp2=z0T∑z0+2z0T∑(z1−z0)rp+(z1−z0)T∑(z1−z0)rp2
(2)一阶条件:

(3)将 z p = z 0 + ( z 1 − z 0 ) r ‾ p z_p=z_0+(z_1-z_0)\overline r_p zp=z0+(z1−z0)rp带入上式即可求出 r ‾ p \overline r_p rp
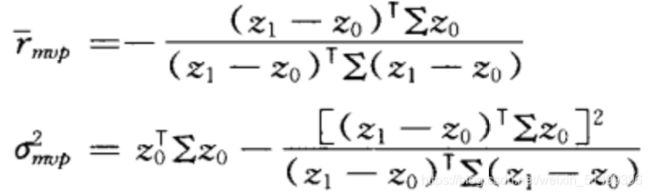
经过一系列推导, r p = a / c r_p=a/c rp=a/c 其中 a = l T ∑ − a=l^T∑^- a=lT∑− 1 r ‾ ^1\overline r 1r, c = l T ∑ − c=l^T∑^- c=lT∑− 1 l ^1l 1l
2、 MVP的性质
性质一:要使任意的组合p与方差最小组合的组合是方差前沿组合(最优组合),即找到两个组合的组合中方差最小的,那么该组合选择一定是方差最小组合,即组合p的权重为0.,且满足 V a r ( r ~ m ) = C o v ( r ~ p , r ~ m ) Var(\tilde r_m)=Cov(\tilde r_p,\tilde r_m) Var(r~m)=Cov(r~p,r~m).
证明: A r g m i n V a r [ a r ~ p + ( 1 − a ) r ~ m Argmin Var[a\tilde r_p+(1-a)\tilde r_m ArgminVar[ar~p+(1−a)r~m v _v v p ] _p] p]
V a r [ a r ~ p + ( 1 − a ) r ~ m Var[a\tilde r_p+(1-a)\tilde r_m Var[ar~p+(1−a)r~m v _v v p ] = a 2 V a r ( r ~ p ) + ( 1 − a ) 2 V a r ( r ~ m ) + 2 a ( 1 − a ) C o v ( r ~ p , r ~ m ) _p]=a^2Var(\tilde r_p) +(1-a)^2Var(\tilde r_m)+2a(1-a)Cov(\tilde r_p,\tilde r_m) p]=a2Var(r~p)+(1−a)2Var(r~m)+2a(1−a)Cov(r~p,r~m)
一阶条件:
a V a r ( r ~ p ) − ( 1 − a ) V a r ( r ~ m ) + ( 1 − 2 a ) C o v ( r ~ p , r ~ m ) aVar(\tilde r_p) -(1-a)Var(\tilde r_m)+(1-2a)Cov(\tilde r_p,\tilde r_m) aVar(r~p)−(1−a)Var(r~m)+(1−2a)Cov(r~p,r~m) =0
方差最小,显然取a=0,此时满足, V a r ( r ~ m ) = C o v ( r ~ p , r ~ m ) Var(\tilde r_m)=Cov(\tilde r_p,\tilde r_m) Var(r~m)=Cov(r~p,r~m).
性质二:对于任意MVF组合(非MVP),一定存在一个NVF组合ZCP(0相关组合),有 C o v ( r ~ p , r ~ z Cov(\tilde r_p,\tilde r_z Cov(r~p,r~z c _c c p ) = 0 _p)=0 p)=0
证明:我们考虑组合p,q的协方差=0是否有解。
C o v ( r ~ p , r ~ q ) = z p T ∑ z q = [ z 0 + r ‾ p ( z 1 − z 0 ) ] T ∑ [ z 0 + r ‾ q ( z 1 − z 0 ) ] = 0 Cov(\tilde r_p,\tilde r_q)=z_p^T\sum z_q=[z_0+\overline r_p(z_1-z_0)]^T\sum[z_0+\overline r_q(z_1-z_0)]=0 Cov(r~p,r~q)=zpT∑zq=[z0+rp(z1−z0)]T∑[z0+rq(z1−z0)]=0
给定p,有 z q = z_q= zq= z 0 T ∑ z p ( z 1 − z 0 ) T ∑ z p z_0^T\sum z_p\over (z_1-z_0)^T\sum z_p (z1−z0)T∑zpz0T∑zp
其中 z 0 , z 1 − z 0 z_0,z_1-z_0 z0,z1−z0都是均值方差前沿组合,其与最小方差组合的组合,协方差为0,即上式分子和分母均不为0.所以均值方差前沿上的每一个组合都对应存在一个0相关组合。
12.2.5 均值方差有效组合MVE
观察均值方差前沿组合,容易发现,MVF的上半沿在均值上占优于下半沿,所以我们通常研究上半沿,也叫做均值方差有效组合MVE(Mean Variance Efficient Portfolios)
12.2.6 均值方差前沿组合和任意组合关系(CAPM)
若p为均值方差前沿组合MVF,那么对于任意组合q我们有
r ‾ q − r ‾ z \overline r_q-\overline r_z rq−rz c _c c p = β p _p=β_p p=βp q _q q ( r ‾ p − r ‾ z (\overline r_p-\overline r_z (rp−rz c _c c p ) _p) p) 其中 β p β_p βp q = C o v ( r ~ p , r ~ q ) / σ p 2 _q=Cov(\tilde r_p,\tilde r_q)/σ_p^2 q=Cov(r~p,r~q)/σp2
看到不必是无风险证券组合,0相关组合也满足该收益率关系。
证明:
(1)先计算组合q的期望收益率
z p z_p zp是均值方差前沿组合,那么其满足一阶条件:
∑ z p − λ r r ‾ − λ 1 l = 0 ∑z_p-λ_r\overline r-λ_1l=0 ∑zp−λrr−λ1l=0 转置后 z p T ∑ − λ r r ‾ T − λ 1 l T = 0 z_p^T∑-λ_r\overline r^T-λ_1l^T=0 zpT∑−λrrT−λ1lT=0
计算两个组合p,q的协方差右乘 z q z_q zq得:
z p T ∑ z q − λ r r ‾ T z q − λ 1 l T z q = 0 z_p^T∑z_q-λ_r\overline r^Tz_q-λ_1l^Tz_q=0 zpT∑zq−λrrTzq−λ1lTzq=0
C o v ( r ~ p , r ~ q ) = z p T ∑ z q = λ r r ‾ T z q + λ 1 l T z q = λ r r ‾ q + λ 1 Cov(\tilde r_p,\tilde r_q)=z_p^T∑z_q=λ_r\overline r^Tz_q+λ_1l^Tz_q=λ_r\overline r_q+λ_1 Cov(r~p,r~q)=zpT∑zq=λrrTzq+λ1lTzq=λrrq+λ1
KKT条件( λ r > 0 λ_r>0 λr>0,约束=0),则我们有
r ‾ q = \overline r_q= rq= C o v ( r ~ p , r ~ q ) − λ 1 λ r Cov(\tilde r_p,\tilde r_q)-λ_1 \over λ_r λrCov(r~p,r~q)−λ1 (1)
(2)下面根据条件计算两个λ算子。
对于MVF组合 r ‾ p = \overline r_p= rp= C o v ( r ~ p , r ~ p ) − λ 1 λ r Cov(\tilde r_p,\tilde r_p)-λ_1 \over λ_r λrCov(r~p,r~p)−λ1 =- λ 1 λ r λ_1\overλ_r λrλ1+ σ p 2 λ r σ_p^2 \over λ_r λrσp2
对于0相关组合 r ‾ z = \overline r_z= rz= C o v ( r ~ p , r ~ z ) − λ 1 λ r Cov(\tilde r_p,\tilde r_z)-λ_1 \over λ_r λrCov(r~p,r~z)−λ1 =- λ 1 λ r λ_1\overλ_r λrλ1 (2)
r ‾ p = r ‾ z + \overline r_p=\overline r_z+ rp=rz+ σ p 2 λ r σ_p^2 \over λ_r λrσp2
则 1 λ r 1\overλ_r λr1= ( r ‾ p − r ‾ z ) (\overline r_p-\overline r_z) (rp−rz) 1 σ p 2 1\over σ_p^2 σp21 (3)
将(2)(3)带入(1)有 r ‾ q − r ‾ z \overline r_q-\overline r_z rq−rz c _c c p = β p _p=β_p p=βp q _q q ( r ‾ p − r ‾ z (\overline r_p-\overline r_z (rp−rz c _c c p ) _p) p) 得证。
12.3 存在无风险证券时的CAPM
12.3.1 存在无风险证券时的组合选择:CML
1、优化问题
给定无风险利率,那么我们前面证券的期望收益率向量转变为超额期望收益率向量即 η ‾ = r ‾ − r F l \overline\eta=\overline r-r_Fl η=r−rFl,对应的组合期望收益率也变为超额期望收益率 η ‾ p = r ‾ p − r F l \overline\eta_p=\overline r_p-r_Fl ηp=rp−rFl,所以优化问题变为:
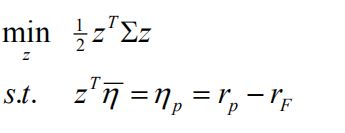
2、求解
(1)建立拉格朗日函数 L = 1 / 2 z T ∑ z + λ ( η ‾ p − z T η ‾ ) L = 1/2z^T\sum z+λ(\overline\eta_p-z^T\overline\eta) L=1/2zT∑z+λ(ηp−zTη)
(2)F.O.C:
∑ z − λ η ‾ = 0 \sum z-λ\overline\eta=0 ∑z−λη=0
η ‾ p − z T η ‾ = 0 \overline\eta_p-z^T\overline\eta=0 ηp−zTη=0
(3)解:
z p = z_p= zp= η ‾ p η ‾ T ∑ − η ‾ \overline\eta_p\over\overline\eta ^T\sum^-\overline\eta ηT∑−ηηp ∑ − η ‾ \sum^-\overline\eta ∑−η
这里假设: η ‾ T ∑ − η ‾ \overline\eta ^T\sum^-\overline\eta ηT∑−η>0即超额收益率为正。这样,我们就得到了存在无风险证券组合时的均值方差前沿。
3、解的讨论:切点组合
(1)当 η ‾ p = 0 \overline \eta_p=0 ηp=0时,组合为无风险资产,所以 z p = 0 , 即 风 险 证 券 组 合 权 重 为 0 z_p=0,即风险证券组合权重为0 zp=0,即风险证券组合权重为0
(2)当 η ‾ T = \overline \eta_T= ηT= η T ∑ − η ‾ l T ∑ − η ‾ \eta ^T\sum^-\overline\eta\over l ^T\sum^-\overline\eta lT∑−ηηT∑−η 类似前面只有风险证券时的b/a,我们假定切点组合的超额期望收益率大于0,那么 l T ∑ − η ‾ l ^T\sum^-\overline\eta lT∑−η>0,即 r ‾ T ∑ − l l T ∑ − l \overline r^T\sum^- l\over l^T\sum^-l lT∑−lrT∑−l > r F >r_F >rF,即a/c最小方差组合收益率大于无风险收益率。
切点组合时有 l T z T = 1 l^Tz_T=1 lTzT=1即只有风险证券组合。我们把这个证券称作切点组合此时, z T = z_T= zT= 1 l T ∑ − η ‾ 1\over l^T\sum^-\overline\eta lT∑−η1 ∑ − η ‾ \sum^-\overline\eta ∑−η
(3)显然其他情况都是这两个组合的组合,且 l T z p = a p ≠ 1 l^Tz_p=a_p\not=1 lTzp=ap=1
a p = l T z p = l T a_p=l^Tz_p=l^T ap=lTzp=lT η ‾ p η ‾ T ∑ − η ‾ \overline\eta_p\over\overline\eta ^T\sum^-\overline\eta ηT∑−ηηp ∑ − η ‾ \sum^-\overline\eta ∑−η = η ‾ p =\overline\eta_p =ηp l T ∑ − η ‾ η ‾ ∑ − η ‾ l^T \sum^-\overline\eta\over\overline\eta \sum^-\overline\eta η∑−ηlT∑−η = = = η ‾ p η ‾ T \overline\eta_p\over\overline\eta_T ηTηp
所以我们找到了任意MVF组合和切点组合的关系 z p = a p z T z_p=a_pz_T zp=apzT,任意组合的风险证券是切点组合,即任意MVF组合是无风险证券和切点组合的组合。
12.3.2 几何方法推导两基金分离:CML
上一节,我们用解析方法推导出,任意MVF组合都是无风险证券和切点组合的组合,这一节,我们利用前面只有风险证券的结论结合几何方法推导存在无风险证券时的两基金分离。
1、风险证券的构建:测度变换
我们假设MVF组合中风险证券的权重为 a = l T z ≠ 1 a=l^Tz\not=1 a=lTz=1,那么我们就可以通过测度变换,得到 l T q = 1 l^Tq=1 lTq=1即令q= z l T z z\over l^Tz lTzz=z/a.
我们求解市场中只有风险组合q时的MVF,即前面得到的双曲线。
对于存在无风险证券的每一个风险权重向量z都有相应的风险组合q与之对应。
因此z这个组合是处于双曲线上的任意一点。
2、将风险证券和无风险证券组合
两者组合就是二者连线的所有可能结果,如图所示: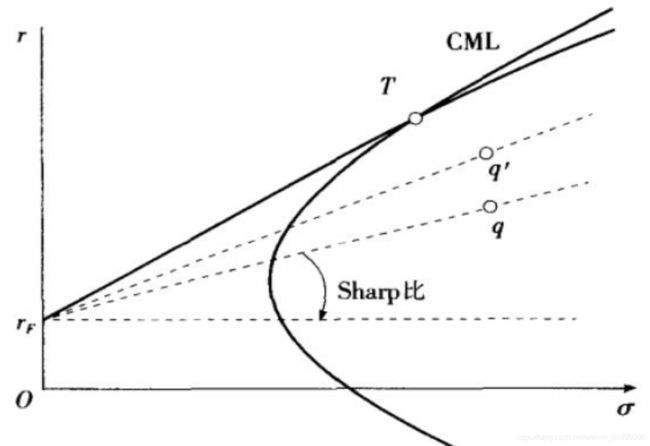
类似于前面的有效前沿组合MVE,存在无风险证券时的有效前沿为切点组合与无风险证券的连线。因为该直线占优与下方的点,即具有最大的期望收益率或标准差,这条直线就是经常听到的资本市场线(CML),图中夹角部分的正切值即每条直线的斜率就是夏普比率,用公式表示为: r ‾ q − r ‾ F σ q \overline r_q-\overline r_F \over σ_q σqrq−rF意味着单位风险的风险溢价。切点组合具有最高的夏普比率即单位风险溢价最高,这正是参与者希望选择的点。(所以前面由最优化条件得到的风险组合是切点组合即所有参与者都会选择这一点与无风险证券组合)
12.3.3 任意组合的定价公式:

对于存在无风险证券的情况,我们要证明: η ‾ q = β p \overline\eta_q=β_p ηq=βp q η ‾ p _q\overline\eta _p qηp
证明:所有包含β的定价公式,都要从方差和协方差推导
(1)考虑p,q收益率的协方差:
C o v ( r ~ p , r ~ q ) = z p T ∑ z q Cov(\tilde r_p,\tilde r_q)=z_p^T∑z_q Cov(r~p,r~q)=zpT∑zq
(2)若p是MVE组合,
那么 z p T = z_p^T= zpT= η ‾ p η ‾ T ∑ − η ‾ \overline\eta_p\over\overline\eta ^T\sum^-\overline\eta ηT∑−ηηp η ‾ T ∑ − \overline\eta^T\sum^- ηT∑−
z p T ∑ z q = z_p^T∑z_q= zpT∑zq= η ‾ p η ‾ T ∑ − η ‾ \overline\eta_p\over\overline\eta ^T\sum^-\overline\eta ηT∑−ηηp η ‾ T ∑ − ∑ z q = \overline\eta^T\sum^-∑z_q= ηT∑−∑zq= η ‾ p η ‾ q η ‾ T ∑ − η ‾ \overline\eta_p\overline\eta_q\over\overline\eta ^T\sum^-\overline\eta ηT∑−ηηpηq
(3)q=p,我们有:
V a r ( r ~ p ) = Var(\tilde r_p)= Var(r~p)= η ‾ p 2 η ‾ T ∑ − η ‾ \overline\eta_p^2\over\overline\eta ^T\sum^-\overline\eta ηT∑−ηηp2
所以 η ‾ p C o v ( r ~ p , r ~ q ) V a r ( r ~ p ) \overline\eta_pCov(\tilde r_p,\tilde r_q)\over Var(\tilde r_p) Var(r~p)ηpCov(r~p,r~q) = η ‾ q =\overline\eta_q =ηq
即 η ‾ q = β p \overline\eta_q=β_p ηq=βp q η ‾ p _q\overline\eta _p qηp
(4)把p选为切点组合
r ‾ q − r F = β T \overline r_q-r_F=β_T rq−rF=βT, q ( r ‾ T − r F ) _q(\overline r_T-r_F) q(rT−rF)
所以,在均值方差偏好世界,投资者只会选择切点组合和无风险证券的组合。
风险由它对切点组合风险的贡献大小来度量即β。证券的风险溢价为切点组合的风险溢价乘以证券的风险(β)来度量。切点组合的β=1.

