树的基本操作

树的概念

树是什么

众所周知，树在生活中无处不在。大自然中的树各式各样。

而我们在数据结构中所探讨的与此有相似之处，又与此有莫大的不同。我们数据结构吗，要从树这种结构说起。

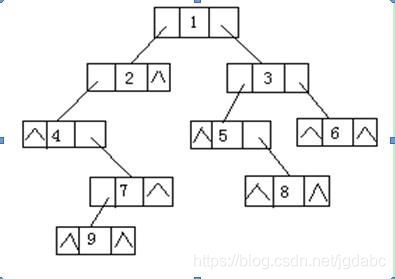
树的定义:
树又称tree,它是个结点的有限集。
空树：当tree为空时称为空树
树可以只有一个根结点

我们数据结构的树根是朝上的
除根结点外，其余结点有且仅有一个前驱。
T中个结点可以有0个或者多个后继

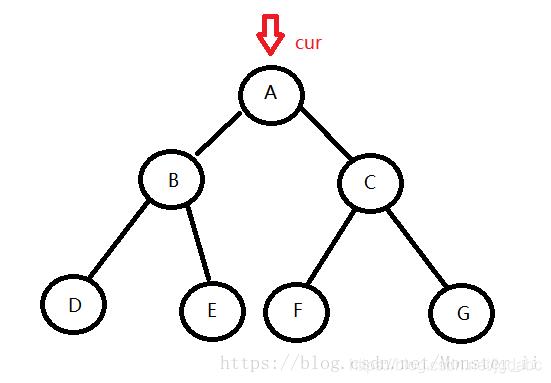
什么是前驱？像图中，A就是B的前驱，B是D的前驱，以此类推。
什么是后继？像图中，B是A的后继，D是B的后继，以此类推。
除根结点外，其余结点可分为若干个互不相交的有限集合。

树的表示

当然，除了树状图之外，我们树还有其他的表示法
凹入表示法

嵌套表示法

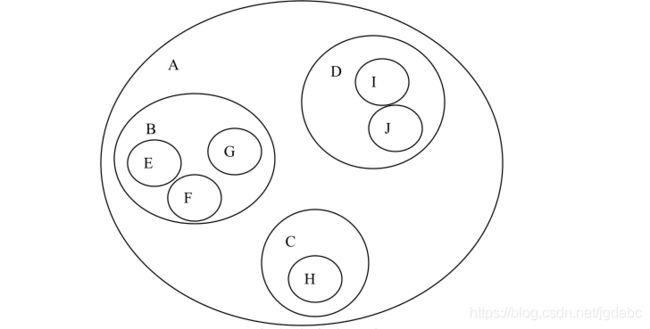
广义表表示法：
(A(B(E(F),G),C,D,(H(I),J,K(L)))

树的相关术语

结点：树中的每个元素可称为树结点。
根：没有前驱的结点可称为根。
结点的度：一个结点含有的子结点的个数称为该结点的度；
叶结点或终端结点：度为0的结点称为叶结点；
非终端结点或分支结点：度不为0的结点；
双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；
孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；
兄弟结点：具有相同父结点的结点互称为兄弟结点；
树的度：一棵树中，最大的结点的度称为树的度；
结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推；
树的高度或深度：树中结点的最大层次；
堂兄弟结点：双亲在同一层的结点互为堂兄弟；
结点的祖先：从根到该结点所经分支上的所有结点；
子孙：以某结点为根的子树中任一结点都称为该结点的子孙。
森林：由m（m>=0）棵互不相交的树的集合称为森林；
无序树：树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树;
有序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树；
二叉树：每个节点最多含有两个子树的树称为二叉树；
满二叉树：叶节点除外的所有节点均含有两个子树的树被称为满二叉树
完全二叉树：有个节点的满二叉树称为完全二叉树
哈夫曼树（最优二叉树）：带权路径最短的二叉树称为哈夫曼树或最优二叉树

二叉树

二叉树的定义

我们比较关注的就是二叉树了

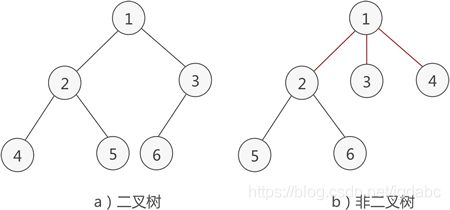
二叉树满足的条件：
1：有序，有顺序，右左右之分。
2：树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2。
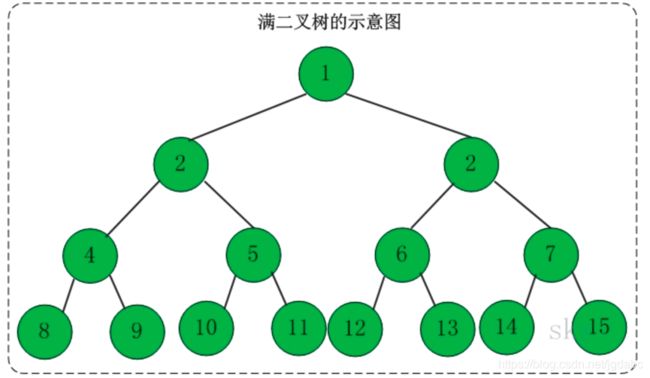
我们来看一个满二叉树

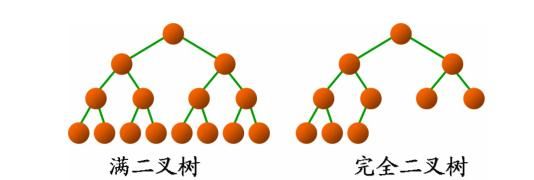
还有一种是完全二叉树，我们将两者对比

可以得到满二叉树的定义：
除了叶子结点，每个结点的度都为 2的二叉树
可以得到完全二叉树的定义：
除去最后一层结点为满二叉树，且最后一层的结点依次从左到右分布的二叉树

二叉树的性质：

1: 二叉树中，第 i 层最多有 2i-1 个结点。
2: 如果二叉树的深度为 K，那么此二叉树最多有 2K-1 个结点。
3:二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。
4:具有 n 个节点的满二叉树的深度为 log2(n+1)。
5：n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。注意，前面的括号表示取整
对于完全二叉树
6：当 i>1 时，父亲结点为结点 [i/2] 。（i=1 时，表示的是根结点，无父亲结点）
7：如果 2i>n（总结点的个数） ，则结点 i 肯定没有左孩子（为叶子结点）；否则其左孩子是结点 2i 。
8:如果 2i+1>n ，则结点 i 肯定没有右孩子；否则右孩子是结点 2i+1

二叉树的存储

首先我们要明白，二叉树是一种非线性结构。
二叉树的存储结构分为两种：

顺序存储

我们需要注意的是，我们的顺序存储二叉树是采用数组的方式的，
我们的顺序存储只适用于完全二叉树。如果想存储其他的树，那就要先进行一个转换。
类似这样
转换

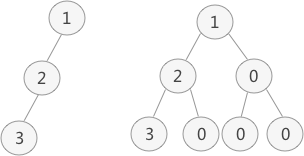
完全二叉树的存储

普通二叉树的存储

可以看到，没有的结点元素，用零给代替了。

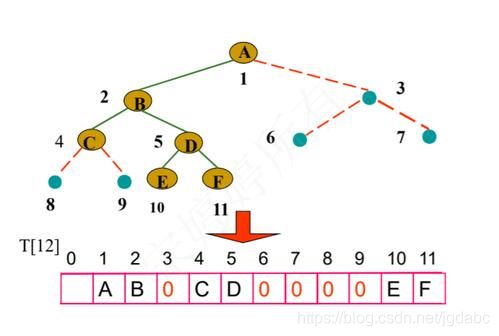
顺序存储只适用于存储完全二叉树，非常浪费空间。

链式存储

链式存储非常容易理解，根据二叉树的结构，我们知道至少需要三部分。

指向左孩子的指针域，指向有孩子的指针域，还有本身的数据域。

我们来看结构代码
下面展示一些 内联代码片。

typedef struct BiTNode{
    TElemType data;//数据域
    struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;

如果需要频繁访问父结点，我们就多定义一个指向父结点的指针即可。
我们来看一个二叉树的完整实现代码
下面展示一些 内联代码片。

include 
#include //这个头文件里有我们需要的malloc函数
#define TElemType int

typedef struct BiTNode{
    TElemType data;//数据域
    struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;

void CreateBiTree(BiTree T){
    T=(BiTNode*)malloc(sizeof(BiTNode));//申请空间
    T->data=1;
    T->lchild=(BiTNode*)malloc(sizeof(BiTNode));
    T->rchild=NULL;
    T->lchild->data=2;            
    T->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
    T->lchild->rchild=NULL;
    T->lchild->lchild->data=3;
    T->lchild->lchild->lchild=NULL;
    T->lchild->lchild->rchild=NULL;
}
int main() {
    BiTree Tree;
    CreateBiTree(Tree);//
    printf("%d",Tree->lchild->lchild->data);
    return 0;
}

链式存储还是非常节约空间的。

二叉树的遍历

二叉树的递归遍历

1: 先序遍历(先根)
先遍历根，再遍历左子树，后遍历右子树
2：中序遍历（中根）
先遍历左子树，再遍历根，后遍历左子树
3：后序遍历（后根）
先遍历左子树，后遍历右子树，再遍历根
4:层次遍历
就是从上到下一层一层的遍历

可以看到。这里的先序遍历还是后序遍历，或者是中序遍历都是相对根结点而言的。

No picture you say a j8 ?
来看图

来看实现算法
我们先定义这个基本的结构
下面展示一些 内联代码片。

typedef char ElemType;
typededf struct node
{
	ElemType data;
	struct node *lchild ,*rchild;

}BitTree;
BitTree *bt;
//先序建立二叉树
BitTree * CreTree(void)
{
	BitTree *bt; ElemType x;
	scanf("%c",&x)
	if(x=="*")
	{
		bt =NULL;
	}
	else 
	{
		bt = (BitTree*)malloc(sizeof(BitTree));
		bt->data =x;
		b>lchild = CreTree();//递归调用
		bt->rchild =CreTree();
		return bt;
}
//先序遍历
void PreOrder(BitTree *bt)
{
if(bt!=NULL)
{
printf("L",bt->data);
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
else
{
	printf("这是一棵空树");
}
}
// 二叉树中序遍历 */
void InOrder(BitTree *bt)
{
if(bt!=NULL)
{
InOrder(bt->lchild);
printf("L",bt->data);
InOrder(bt->rchild);
}
}
// 二叉树后序遍历 */
void PostOrder(BitTree *bt)
{
if(bt!=NULL)
{
PostOrder(bt->lchild);
PostOrder(bt->rchild);
printf("L",bt->data);
}
}

main()
{
BitTree *T;
T=CreTree();
printf("\n输出二叉树先序遍历序列：\n");
PreOrder(T);
printf("\n输出二叉树中序遍历序列：\n");
InOrder(T);
printf("\n输出二叉树后序遍历序列：\n");
PostOrder(T);
printf("\n");
system("pause");
}

}

注意：这里的递归在二叉树这里体现的淋漓尽致

二叉树的非递归遍历

非递归遍历相比递归遍历比较麻烦一点，因为要涉及与栈有关的操作

no picture you see a j8?

注： 下面的图片是从网上找来的，为了形象描述非递归遍历的过程

以前序遍历来说明

1：首先定义一个cur指针，指向当前要访问的节点

2：如果结点不为空，则将该结点的数据输出来，并将结点的地址压栈

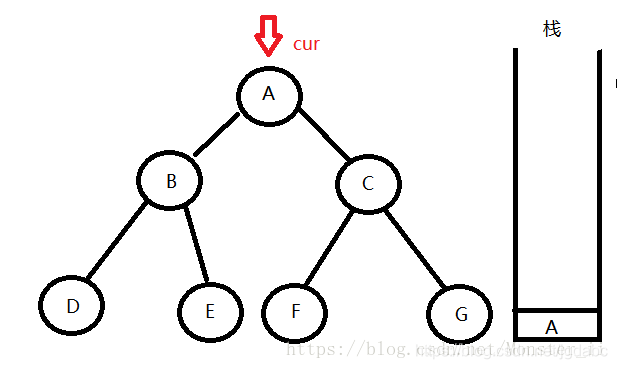
3:访问B的其左孩子，发现依然不是空节点，则执行与A一样的操作

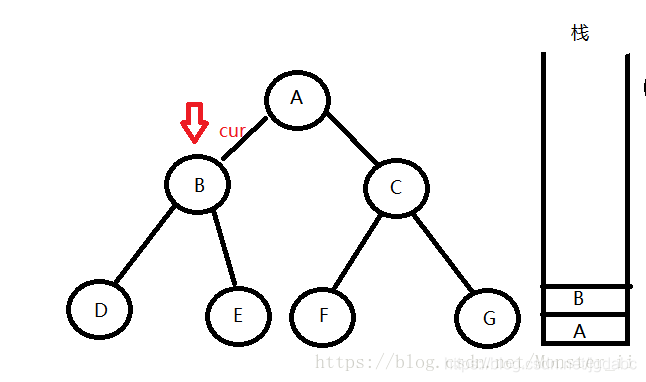
3:同理

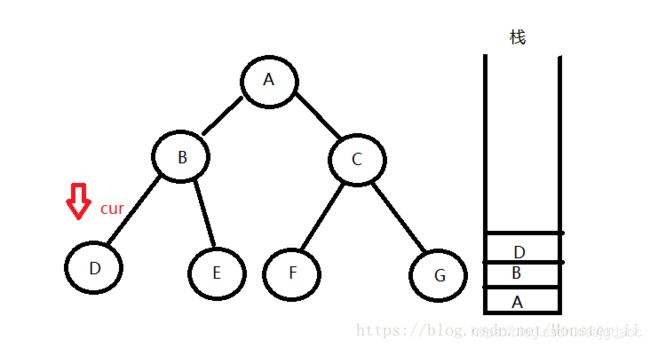
4：访问D的左孩子，发现为空，便从栈中拿出栈顶结点top，让cur = top->right,便访问到了D的右孩子。

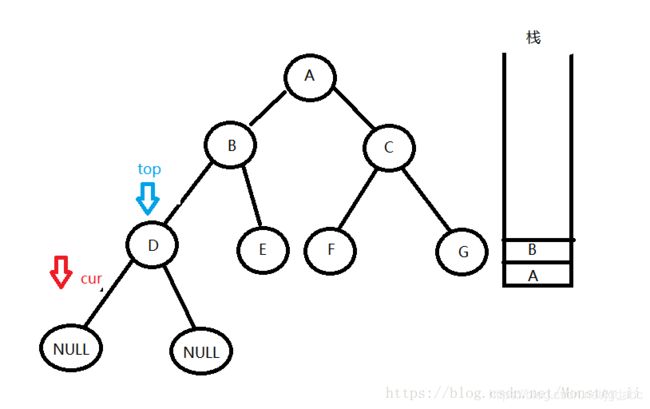
5：然后D的有孩子还是空。继续执行相似的操作
从栈中拿出栈顶结点top，让cur = top->right

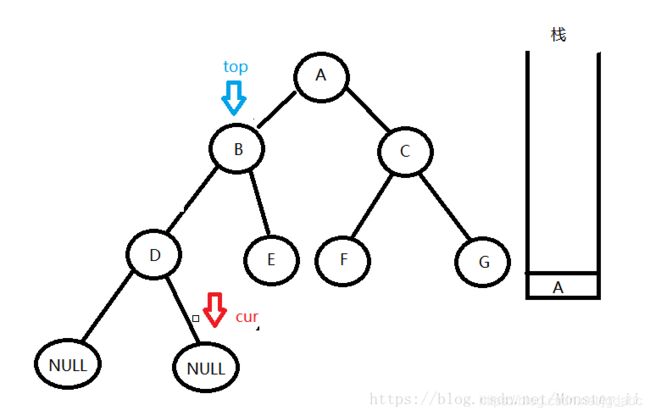
6:依次

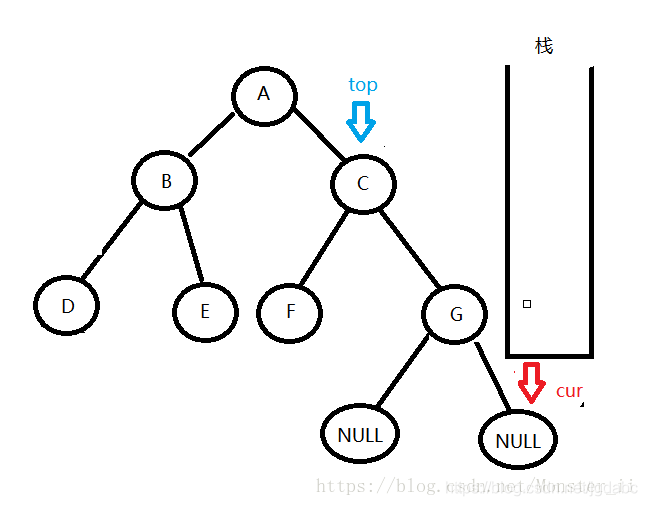
后面的执行类似的操作。
有关非递归遍历的请参考这里 ，另一位博主的详细解释。二叉树非递归遍历

线索二叉树

线索二叉树的概念

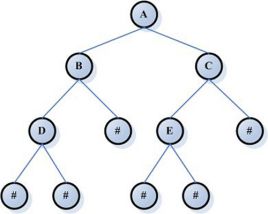
我们先看二叉链表

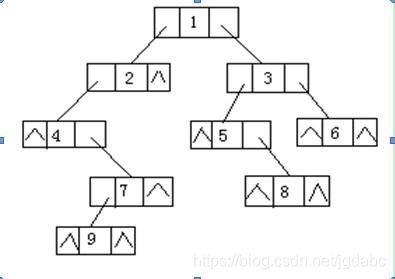
可以看到这里有空指针域。我们可以看到一共有九个结点，而又十个空指针域。同理，那么，n个结点就有n+1个空指针域。我们何不将这些空指针域利用起来？
就像这样

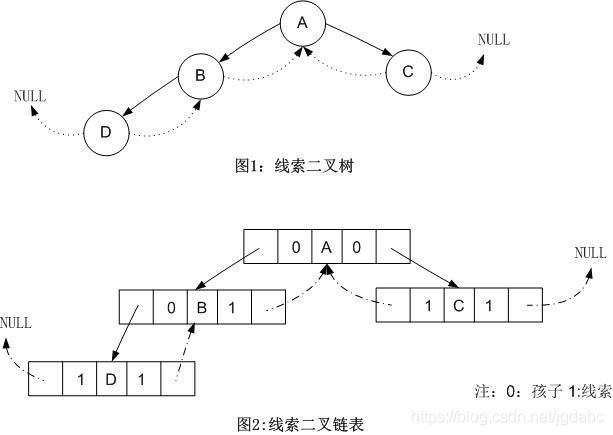
我们可以看到，空指针域可以得到利用。同时，这样做还可以很方便的找到结点的前驱或者是后继结点。

二叉树线索的规则

其实二叉树的线索化可以理解为遍历的过程
我们来以中序线索来实现中序线索二叉树
（1）如果ptr->lchild为空，则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱；
（2）如果ptr->rchild为空，则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继；

(1) ltag为0时指向该结点的左孩子，为1时指向该结点的前驱；
（2）rtag为0时指向该结点的右孩子，为1时指向该结点的后继；
我们来看结构实现

typedef struct TBTNode{
    char data;
    int ltag,rtag;//这里其实为左右孩子的标记
    struct TBTNode *lchild;
    struct TBTNode *rchild;
}TBTNode;

线索化的规则是：左线索指针指向当前结点在中序遍历序列中的前驱结点，右线索指针指向后继结点。因此我们需要一个指针p指向当前正在访问的结点，pre指向p的前驱结点，p的左线索指针如果存在的话直接指向pre（也就是前驱结点），pre的右线索如果存在则指向p（也就是直接后继）。

我们来看图

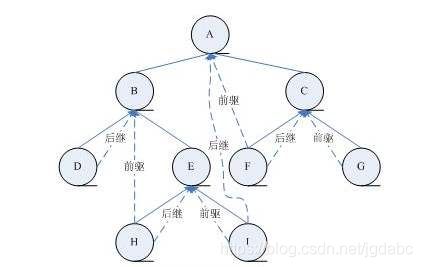
我们先来看这棵二叉树的中序遍历结果
就是 DBHEIAFCG
我们这样写出后就很容易看出相应结点的前驱和后继
再来看图的线索化，就很好将线索化的二叉树得到验证。
我们来看算法

void InThread(TBTNode *p, TBTNode *&pre){
    if (p != null)
    {
        InThread(p->lchild, pre);    //对左孩子递归，自然第一个操作的结点为最左下结点（不一定为叶结点），如上图为D
        if (p->lchild == NULL)
        {
            p->lchild = pre;
            p->ltag = 1;
        }
        if (pre != NULL && pre->rchild == NULL)
        {
            pre->rchild = p;
            pre->rtag = 1;
        }
        pre = p; //当p将要离开一个访问过的结点时，pre指向p，所以p指向新结点时，pre显然是此时p的直接前驱
        p = p->rchild; //p指向右孩子，准备将右子树线索化
        InThread(p, pre);
    }
}

数据结构加算法等于程序。因此掌握掌握数据结构对于程序设计是非常重要的。学过的东西常常会有忘记的时候，当学过数据结构这种思想后，不能与程序设计很好的结合，也是很容易忘记的。很多东西需要实际的练习，计算机相关的设计思想也是如此。

欢迎继续关注
—jgdabc