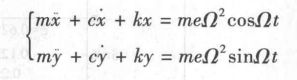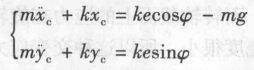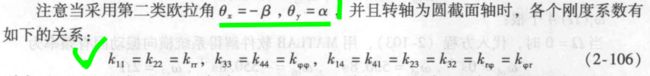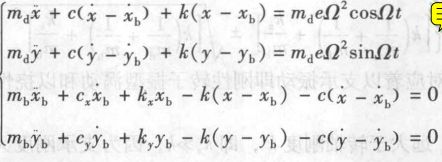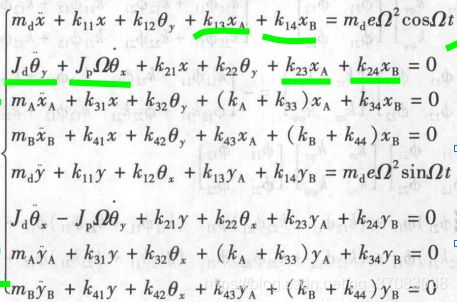单盘转子的稳态涡动
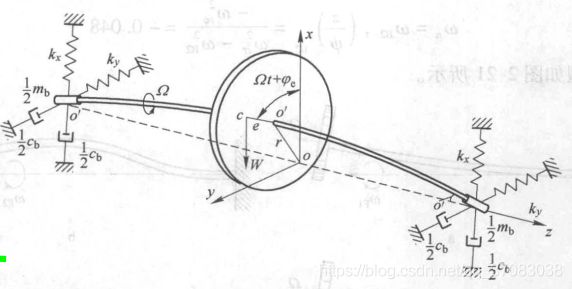
1.刚性支撑+对称转子
1.1质量偏心+纵向放置
将Jeffcott转子立起来避免了由于质量偏心加重力产生的静弯曲。
忽略轴向位移。
转子扭转刚度无限大。
(x,y)为圆盘形心o'的位置，得出形心的涡动方程。
用复数表示该方程组 z=x+iy
1.2质量偏心+横向放置
质心c的运动方程
也可以将其变换为形心o'的涡动方程
质心c的转动方程
注：由质心运动方程推导形心的涡动方程
Xc = X + e*cosφ，Yc = Y + e*sinφ
对其两边求两阶导
Xc'' = X'' - eφ''*sinφ - eφ'**2*cosφ，Yc'' = Y'' - eφ''*cosφ - eφ'**2*sinφ
因为是稳态，所以角加速度φ''=0。
将这些式子带入质心的运动方程
mX'' + kX = meφ'**2*cosφ - mg
mY'' + kY = meφ'**2*sinφ
转速为Ω，则φ=Ωt，φ'=Ω
mX'' + kX = meΩ**2*cosΩt - mg
mY'' + kY = meΩ**2*sinΩt
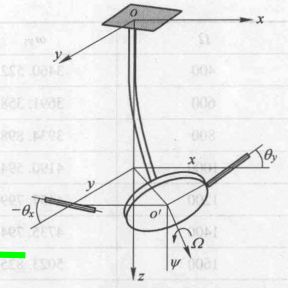
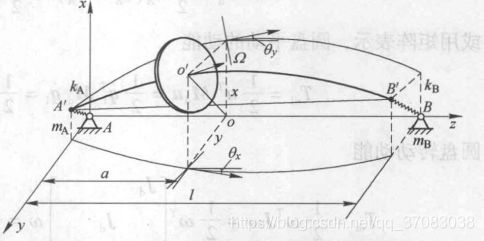
2.刚性支撑+偏置转子
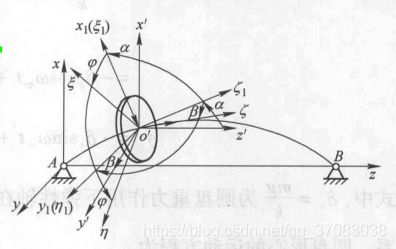
与对称转子对转轴只作用有力 不同的是，圆盘对转轴还作用有力矩。
F与M的方向如图：
圆盘给转轴的力
Fx = K11*x + K12*α
Mx = K21*x + K22*α
Fy = K11*y + K12*β
-My = K21*y + K22*β 这里的My取负号，是因为方向沿x轴负方向
注：K11 = Fx/x K12 = Fx/α K21 = Mx/x K22 = Mx/α，K12=K21
由于是圆截面，则Fx/x=Fy/y，Fx/α = Fy/β，Mx/x = My/y，Mx/α=My/β
如：K11是指 沿x方向移动单位位移时，需要在x方向施加的力。也就等于，沿y方向移动单位位移时，需要在y方向施加的力。
圆盘形心o'的运动方程
随圆盘转动的坐标系o'ξ1η1ζ下的摆动方程
稳态，β为小角度，忽略二阶及以上的非线性项，则上述方程化简为：
随动坐标系中的外力矩不容易计算
平动坐标系o'x'y'z'下的摆动方程
3.刚性支撑+悬臂转子
其涡动方程与偏置转子相同
注：涡动方程就是形心的运动微分方程，如果圆盘还有偏摆，再加上形心的摆动微分方程。
4. 弹性支撑+对称转子
形心运动方程
5. 弹性支撑+偏置转子
