机器学习-白板推导系列笔记(二十一)-RBM
此文章主要是结合哔站shuhuai008大佬的白板推导视频:受限玻尔兹曼机_155min
全部笔记的汇总贴:机器学习-白板推导系列笔记
一、背景介绍
RBM(Restricted Boltzmann Machine)
(一)玻尔兹曼机
玻尔兹曼机(Boltzmann Machine)可以说它就是一个马尔科夫随机场(Markov Random Field),简单来说就是一个无向图模型,是一种随机神经网络,借鉴了模拟退火思想,因为使用了玻尔兹曼分布作为激活函数,所以称为玻尔兹曼机。
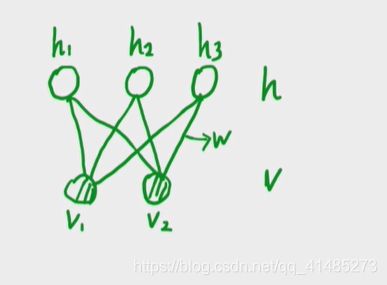
如下图所示,将无向图中的节点分为两类,阴影的节点为Observed Variable(用 v v v表示),另一类为Hidden Variable(用 h h h表示)

(二)因子分解
既然说玻尔兹曼机是一种特殊的马尔科夫随机场,我们首先回顾一下马尔科夫随机场的因子分解。
马尔科夫随机场的因子分解是基于最大团的,其中:
C i : 最 大 团 , ψ i ( x c i ) : 势 函 数 ( p o t e n t i a l f u n c t i o n ) Z : 归 一 化 因 子 ( 配 分 函 数 p a r t i t i o n f u n c t i o n ) C_i:最大团,\psi_i(x_{ci}):势函数(potential\;function) Z:归一化因子(配分函数partition\;function) Ci:最大团,ψi(xci):势函数(potentialfunction)Z:归一化因子(配分函数partitionfunction)
P ( x ) = 1 Z ∏ i = 1 K ψ i ( x c i ) P(x)=\frac1Z\prod^K_{i=1}\psi_i(x_{ci}) P(x)=Z1i=1∏Kψi(xci) S . t . : ψ i 严 格 大 于 0 Z = ∑ x ∏ i = 1 K ψ i ( x c i ) = ∑ x 1 ∑ x 2 ⋯ ∑ x p ∏ i = 1 K ψ i ( x c i ) S.t.:\psi_i严格大于0\\Z=\sum_x\prod^K_{i=1}\psi_i(x_{ci})=\sum_{x_1}\sum_{x_2}\cdots\sum_{x_p}\prod^K_{i=1}\psi_i(x_{ci}) S.t.:ψi严格大于0Z=x∑i=1∏Kψi(xci)=x1∑x2∑⋯xp∑i=1∏Kψi(xci)
因 为 ψ i 严 格 大 于 0 , 所 以 我 们 取 ψ i ( x c i ) = exp { − E ( x c i ) } , 其 中 E 为 能 量 函 数 ( E n e r g y F u n c t i o n ) 因为\psi_i严格大于0,所以我们取\psi_i(x_{ci})=\exp\{-E(x_{ci})\},其中E为能量函数(Energy\;Function) 因为ψi严格大于0,所以我们取ψi(xci)=exp{ −E(xci)},其中E为能量函数(EnergyFunction)
所以, P ( x ) = 1 Z ∏ i = 1 K ψ i ( x c i ) = 1 Z exp { − ∑ i = 1 K E ( x c i ) } ⏟ 指 数 族 分 布 P(x)=\frac1Z\prod^K_{i=1}\psi_i(x_{ci})=\underset{指数族分布}{\underbrace{\frac1Z\exp\{-\sum^K_{i=1}E(x_{ci})\}}} P(x)=Z1i=1∏Kψi(xci)=指数族分布 Z1exp{ −i=1∑KE(xci)}
所以,我们将最大团结合到 x x x中去,可以得到, P ( x ) = 1 Z exp { − E ( x ) } P(x)=\frac1Z\exp\{-E(x_{})\} P(x)=Z1exp{ −E(x)}
这就是玻尔兹曼分布(Boltzmann Distribution)或者吉布斯分布(Gibbs Distribution)
(三)玻尔兹曼分布
这是一个统计物理学的概念,是一个物理系统,具体可以看看视频的讲解,这篇文章也可以看看:玻尔兹曼机。
二、模型表示
(一)RBM的模型推导
对于 x x x,我们可以令 x = ( x 1 , x 2 , ⋯ , x p ) T x=(x_1,x_2,\cdots,x_p)^T x=(x1,x2,⋯,xp)T,也可以将 x x x分为隐变量和观测变量两部分,即 x = ( h v ) x=\left(\begin{matrix} h\\v\end{matrix}\right ) x=(hv),其中,
h = ( h 1 , h 2 , ⋯ , h m ) T v = ( v 1 , v 2 , ⋯ , v p ) T m + n = p h=(h_1,h_2,\cdots,h_m)^T\\v=(v_1,v_2,\cdots,v_p)^T\\m+n=p h=(h1,h2,⋯,hm)Tv=(v1,v2,⋯,vp)Tm+n=p
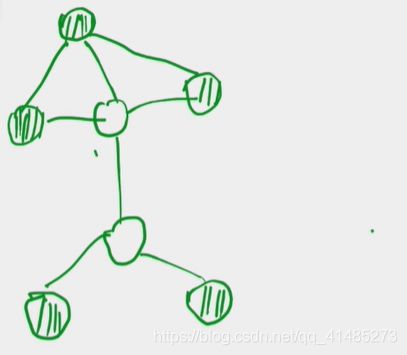
Boltzmann machine的问题:Inference。精确推断几乎不可能,近似推断计算量过大。因此需要对这个模型进行简化,也就引出了受限玻尔兹曼机(Restricted Boltzmann Machine),即只在 h , v h,v h,v之间有连接, h , v h,v h,v内部无连接。
所以, P ( x ) = 1 Z exp { − E ( x ) } P(x)=\frac1Z\exp\{-E(x_{})\} P(x)=Z1exp{ −E(x)}可以化为:
P ( v , h ) = 1 Z exp { − E ( v , h ) } P(v,h)=\frac1Z\exp\{-E(v,h)\} P(v,h)=Z1exp{ −E(v,h)}
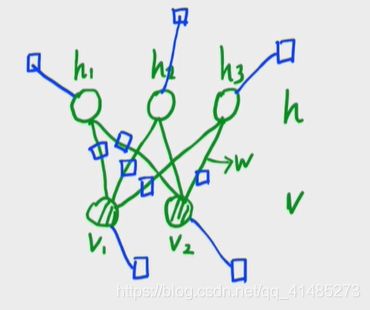
我们假设 E ( v , h ) = − ( h T w v + α T v + β T h ) E(v,h)=-(h^Twv+\alpha^T v+\beta^T h) E(v,h)=−(hTwv+αTv+βTh),所以,
P ( v , h ) = 1 Z exp { h T w v + α T v + β T h } = 1 Z exp { h T w v } ⋅ exp { α T v } ⋅ exp { β T h } P(v,h)=\frac1Z\exp\{h^Twv+\alpha^T v+\beta^T h\}\\=\frac1Z\exp\{h^Twv\}\cdot\exp\{\alpha^T v\}\cdot\exp\{\beta^T h\} P(v,h)=Z1exp{ hTwv+αTv+βTh}=Z1exp{ hTwv}⋅exp{ αTv}⋅exp{ βTh}
可以参考白板推导系列笔记(九)-概率图模型中的因子图(factor graph view),可以发现上式中的每一项都对应一个因子。
所以,RBM的pdf为:
P ( v , h ) = 1 Z exp ( h T w v ) ⋅ exp ( α T v ) ⋅ exp ( β T h ) = 1 Z ∏ i = 1 m ∏ j = 1 n exp ( h i w i j v j ) ⏟ e d g e ∏ j = 1 n exp ( α j v j ) ⏟ n o d e v ∏ i = 1 m exp ( β i h i ) ⏟ n o d e h ⏟ f a c t o r 其 中 , w , α , β 均 为 参 数 P(v,h)=\frac1Z\exp(h^Twv)\cdot\exp(\alpha^T v)\cdot\exp(\beta^T h)\\=\frac1Z\underset{factor}{\underbrace{\underset{edge}{\underbrace{\prod^m_{i=1}\prod^n_{j=1}\exp(h_iw_{ij}v_j)}}\underset{node\;v}{\underbrace{\prod^n_{j=1}\exp(\alpha_jv_j)}}\underset{node\;h}{\underbrace{\prod^m_{i=1}\exp(\beta_ih_i)}}}}\\其中,w,\alpha,\beta均为参数 P(v,h)=Z1exp(hTwv)⋅exp(αTv)⋅exp(βTh)=Z1factor edge i=1∏mj=1∏nexp(hiwijvj)nodev j=1∏nexp(αjvj)nodeh i=1∏mexp(βihi)其中,w,α,β均为参数
(二)常见的概率图模型归纳
这一节是一个回顾(可以理解为上帝视角来看学过的所有概率图模型),有不懂的可以翻看之前的内容(我第一次刷的时候,就有一种把知识都串起来了的感觉)。
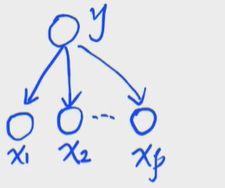
1. Naive Bayes(NB)
朴素贝叶斯假设也就是条件独立性假设。
x i ⊥ x j ∣ y ( i ≠ j ) x_i\perp x_j|y(i\neq j) xi⊥xj∣y(i=j)
2. Gaussian Mixture Model(GMM)
高斯混合模型,引入了隐变量。
3. State Space Model(SSM)
状态空间模型,包括(HMM、Kalman Filter、Particle Filter),也引入了隐变量,有两个假设(a.齐次Markov b.观测独立)
4.Maximum Entropy Markov Model(MEMM)
是MEM(由LR过来)和HMM的一个综合。是一个判别模型,打破了观测独立假设。

5.Condition Random Filed(CRF)
条件随机场是一个判别模型,是一个无向图(MRF),打破了齐次马尔可夫假设。给定 x x x的情况下 y y y是一个马尔可夫随机场。
y ∣ x ∼ M R F y|x\sim MRF y∣x∼MRF
6.Linear Chain-CRF(LC-CRF)
7.Boltzmann Machine(BM)
玻尔兹曼机是无向的,引入了一组隐变量,他的PDF是指数族分布(玻尔兹曼分布、吉布斯分布)。 P ( x ) = 1 Z exp { − E ( x ) } P(x)=\frac1Z\exp\{-E(x_{})\} P(x)=Z1exp{ −E(x)}

x = { v , h } , x 为 观 测 变 量 , h 为 隐 变 量 x=\{v,h\},x为观测变量,h为隐变量 x={ v,h},x为观测变量,h为隐变量
8.Restricted Boltzmann Machine(RBM)
受限玻尔兹曼机首先满足玻尔兹曼机(BM)的所有特点,然后他是条件独立的(组内无连接)。

所以,对比以上的几种概率图模型,大概有以下几个特点(也是各种模型之间的区别):
- 方向(有向/无向) 边 的 角 度 \color{blue}{边的角度} 边的角度
- 离散/连续(连续主要就是和高斯网络的结合) 点 的 角 度 \color{blue}{点的角度} 点的角度
- 条件独立性 边 的 角 度 \color{blue}{边的角度} 边的角度
- 隐变量(有的引入了,有的没有) 点 的 角 度 \color{blue}{点的角度} 点的角度
- 概率密度函数(PDF)是否为指数族分布 结 构 的 角 度 \color{blue}{结构的角度} 结构的角度
三、模型推断
(一)后验概率
x = ( x 1 x 2 ⋮ x p ) = ( h v ) h = ( h 1 h 2 ⋮ h m ) v = ( v 1 v 2 ⋮ v n ) p = m + n x=\left(\begin{matrix} x_1\\x_2\\\vdots\\x_p\end{matrix}\right )=\left(\begin{matrix} h\\v\end{matrix}\right )\;\;h=\left(\begin{matrix} h_1\\h_2\\\vdots\\h_m\end{matrix}\right )\;\;v=\left(\begin{matrix} v_1\\v_2\\\vdots\\v_n\end{matrix}\right )\;\;p=m+n x=⎝⎜⎜⎜⎛x1x2⋮xp⎠⎟⎟⎟⎞=(hv)h=⎝⎜⎜⎜⎛h1h2⋮hm⎠⎟⎟⎟⎞v=⎝⎜⎜⎜⎛v1v2⋮vn⎠⎟⎟⎟⎞p=m+n
P ( x ) = 1 Z exp { − E ( x ) } P(x)=\frac1Z\exp\{-E(x_{})\} P(x)=Z1exp{ −E(x)}
P ( v , h ) = 1 Z exp { − E ( v , h ) } P(v,h)=\frac1Z\exp\{-E(v,h)\} P(v,h)=Z1exp{ −E(v,h)}
E ( v , h ) = − ( h T w v + α T v + β T h ) = − ( ∑ i = 1 m ∑ j = 1 n h i w i j v j + ∑ j = 1 n α j v j + ∑ i = 1 m β i h i ) E(v,h)=-(h^Twv+\alpha^T v+\beta^T h)\\=-(\sum^m_{i=1}\sum^n_{j=1}h_iw_{ij}v_j+\sum^n_{j=1}\alpha_jv_j+\sum^m_{i=1}\beta_ih_i) E(v,h)=−(hTwv+αTv+βTh)=−(i=1∑mj=1∑nhiwijvj+j=1∑nαjvj+i=1∑mβihi)
P ( v , h ) = 1 Z exp ( h T w v ) ⋅ exp ( α T v ) ⋅ exp ( β T h ) = 1 Z ∏ i = 1 m ∏ j = 1 n exp ( h i w i j v j ) ⏟ e d g e ∏ j = 1 n exp ( α j v j ) ⏟ n o d e v ∏ i = 1 m exp ( β i h i ) ⏟ n o d e h ⏟ f a c t o r P(v,h)=\frac1Z\exp(h^Twv)\cdot\exp(\alpha^T v)\cdot\exp(\beta^T h)\\=\frac1Z\underset{factor}{\underbrace{\underset{edge}{\underbrace{\prod^m_{i=1}\prod^n_{j=1}\exp(h_iw_{ij}v_j)}}\underset{node\;v}{\underbrace{\prod^n_{j=1}\exp(\alpha_jv_j)}}\underset{node\;h}{\underbrace{\prod^m_{i=1}\exp(\beta_ih_i)}}}} P(v,h)=Z1exp(hTwv)⋅exp(αTv)⋅exp(βTh)=Z1factor edge i=1∏mj=1∏nexp(hiwijvj)nodev j=1∏nexp(αjvj)nodeh i=1∏mexp(βihi)
目的:Inference → \rightarrow →posterior → p ( h ∣ v ) , p ( v ∣ h ) \rightarrow\;\;p(h|v),p(v|h) →p(h∣v),p(v∣h)
求 p ( h ∣ v ) p(h|v) p(h∣v)
给定 v v v的条件下,所有的 h h h之间是相互独立的。
所以,
p ( h ∣ v ) = ∏ l = 1 m p ( h l ∣ v ) p(h|v)=\prod^m_{l=1}\color{red}{p(h_l|v)} p(h∣v)=l=1∏mp(hl∣v)
p ( h l = 1 ∣ v ) = p ( h l = 1 ∣ h − l , v ) = p ( h l = 1 , h − l , v ) p ( h l = 1 , h − l , v ) + p ( h l = 0 , h − l , v ) {\color{red}{p(h_l=1|v)}}=p(h_l=1|h_{-l},v)\\=\frac{\color{blue}{p(h_l=1,h_{-l},v)}}{\color{grey}{p(h_l=1,h_{-l},v)+p(h_l=0,h_{-l},v)}} p(hl=1∣v)=p(hl=1∣h−l,v)=p(hl=1,h−l,v)+p(hl=0,h−l,v)p(hl=1,h−l,v)
E ( h , v ) = − ( ∑ i = 1 i ≠ l m ∑ j = 1 n h i w i j v j + ∑ j = 1 n h l w i j v j + ∑ j = 1 n α j v j + ∑ i = 1 i ≠ l m β i h i + β l h l ) E(h,v)=-(\sum^m_{i=1\;i\neq l}\sum^n_{j=1}h_iw_{ij}v_j+{\color{green}{\sum^n_{j=1}h_lw_{ij}v_j}}+\sum^n_{j=1}\alpha_jv_j+\sum^m_{i=1\;i\neq l}\beta_ih_i+{\color{green}{\beta_lh_l}}) E(h,v)=−(i=1i=l∑mj=1∑nhiwijvj+j=1∑nhlwijvj+j=1∑nαjvj+i=1i=l∑mβihi+βlhl)将上式中与 h l h_l hl有关的项提出来,发现是一个与 v v v有关的函数,我们不妨令 h l H l ( v ) = ∑ j = 1 n h l w i j v j + β l h l = h l ( ∑ j = 1 n w i j v j + β l ) h_lH_l(v)=\sum^n_{j=1}h_lw_{ij}v_j+\beta_lh_l\\=h_l(\sum^n_{j=1}w_{ij}v_j+\beta_l) hlHl(v)=j=1∑nhlwijvj+βlhl=hl(j=1∑nwijvj+βl)
即 H l ( v ) = ∑ j = 1 n h l w i j v j + β l h l = ∑ j = 1 n w i j v j + β l H_l(v)=\sum^n_{j=1}h_lw_{ij}v_j+\beta_lh_l\\=\sum^n_{j=1}w_{ij}v_j+\beta_l Hl(v)=∑j=1nhlwijvj+βlhl=∑j=1nwijvj+βl
H l ‾ ( h − l , v ) = ∑ i = 1 i ≠ l m ∑ j = 1 n h i w i j v j + ∑ j = 1 n α j v j + ∑ i = 1 i ≠ l m β i h i \overline{H_l}(h_{-l},v)=\sum^m_{i=1\;i\neq l}\sum^n_{j=1}h_iw_{ij}v_j+\sum^n_{j=1}\alpha_jv_j+\sum^m_{i=1\;i\neq l}\beta_ih_i Hl(h−l,v)=i=1i=l∑mj=1∑nhiwijvj+j=1∑nαjvj+i=1i=l∑mβihi
所以, E ( h , v ) = − ( h l H l ( v ) + H l ‾ ( h − l , v ) ) E(h,v)=-(h_lH_l(v)+\overline{H_l}(h_{-l},v)) E(h,v)=−(hlHl(v)+Hl(h−l,v))p ( h l = 1 , h − l , v ) = 1 Z exp { H l ( v ) + H l ‾ ( h − l , v ) } {\color{blue}{p(h_l=1,h_{-l},v)}}=\frac1Z\exp\{H_l(v)+\overline{H_l}(h_{-l},v)\} p(hl=1,h−l,v)=Z1exp{ Hl(v)+Hl(h−l,v)}
p ( h l = 1 , h − l , v ) + p ( h l = 0 , h − l , v ) = 1 Z exp { H l ( v ) + H l ‾ ( h − l , v ) } + 1 Z exp { H l ‾ ( h − l , v ) } {\color{grey}{p(h_l=1,h_{-l},v)+p(h_l=0,h_{-l},v)}}=\frac1Z\exp\{H_l(v)+\overline{H_l}(h_{-l},v)\}+\frac1Z\exp\{\overline{H_l}(h_{-l},v)\} p(hl=1,h−l,v)+p(hl=0,h−l,v)=Z1exp{ Hl(v)+Hl(h−l,v)}+Z1exp{ Hl(h−l,v)}
所以,
p ( h l = 1 ∣ v ) = exp { H l ( v ) + H l ‾ ( h − l , v ) } exp { H l ( v ) + H l ‾ ( h − l , v ) } + exp { H l ‾ ( h − l , v ) } = 1 1 + exp { H l ‾ ( h − l , v ) − ( H l ( v ) + H l ‾ ( h − l , v ) ) } = 1 1 + exp { − H l ( v ) } = σ ( H l ( v ) ) = σ ( ∑ j = 1 n w i j v j + β l ) {\color{red}{p(h_l=1|v)}}=\frac{\exp\{H_l(v)+\overline{H_l}(h_{-l},v)\}}{\exp\{H_l(v)+\overline{H_l}(h_{-l},v)\}+\exp\{\overline{H_l}(h_{-l},v)\}}\\=\frac1{1+\exp\{\overline{H_l}(h_{-l},v)-(H_l(v)+\overline{H_l}(h_{-l},v))\}}\\=\frac1{1+\exp\{-H_l(v)\}}\\=\sigma(H_l(v))\\=\sigma(\sum^n_{j=1}w_{ij}v_j+\beta_l) p(hl=1∣v)=exp{ Hl(v)+Hl(h−l,v)}+exp{ Hl(h−l,v)}exp{ Hl(v)+Hl(h−l,v)}=1+exp{ Hl(h−l,v)−(Hl(v)+Hl(h−l,v))}1=1+exp{ −Hl(v)}1=σ(Hl(v))=σ(j=1∑nwijvj+βl)sigmoid函数: σ ( x ) = 1 1 + e − x \sigma(x)=\frac1{1+e^{-x}} σ(x)=1+e−x1
同理可得:
p ( v ∣ h ) = ∏ l = 1 n p ( v l ∣ h ) p(v|h)=\prod^n_{l=1}p(v_l|h) p(v∣h)=l=1∏np(vl∣h)
联想:RBM → \rightarrow →神经网络
sigmoid → σ ( x ) = 1 1 + e − x \rightarrow \sigma(x)=\frac1{1+e^{-x}} →σ(x)=1+e−x1
(二)边缘概率
目的:Inference → \rightarrow → marginal → p ( v ) \rightarrow\;\;p(v) →p(v)
p ( v ) = ∑ h p ( h , v ) = ∑ h 1 Z exp { − E ( h , v ) } = ∑ h 1 Z exp ( h T w v ) ⋅ exp ( α T v ) ⋅ exp ( β T h ) = ∑ h 1 ∑ h 2 ⋯ ∑ h m 1 Z exp ( h T w v ) ⋅ exp ( α T v ) ⋅ exp ( β T h ) = 1 Z exp ( α T v ) ⋅ ∑ h 1 ∑ h 2 ⋯ ∑ h m exp ( h T w v ) ⋅ exp ( β T h ) = 1 Z exp ( α T v ) ⋅ ∑ h 1 ∑ h 2 ⋯ ∑ h m exp ( ∑ i = 1 m ( h i w i v + β i h i ) ) = 1 Z exp ( α T v ) ⋅ ∑ h 1 ∑ h 2 ⋯ ∑ h m exp ( h 1 w 1 v + β 1 h 1 ) ⋅ exp ( h 2 w 2 v + β 2 h 2 ) ⋯ exp ( h m w m v + β m h m ) = 1 Z exp ( α T v ) ⋅ ∑ h 1 exp ( h 1 w 1 v + β 1 h 1 ) ⋅ ∑ h 2 exp ( h 2 w 2 v + β 2 h 2 ) ⋯ ∑ h m exp ( h m w m v + β m h m ) = 1 Z exp ( α T v ) ⋅ ( 1 + exp ( w 1 v + β 1 ) ) ⋅ ( 1 + exp ( w 2 v + β 2 ) ) ⋯ ( 1 + exp ( w m v + β m ) ) = 1 Z exp ( α T v ) ⋅ exp { log ( 1 + exp ( w 1 v + β 1 ) ) } ⋅ exp { log ( 1 + exp ( w 2 v + β 2 ) ) } ⋯ exp { log ( 1 + exp ( w m v + β m ) ) } = 1 Z exp ( α T v + ∑ i = 1 m log ( 1 + exp ( w i v + β i ) ) ⏟ s o f t p l u s f u n c t i o n ) = 1 Z exp ( α T v + ∑ i = 1 m s o f t p l u s ( w i v + β i ) ) p(v)=\sum_hp(h,v)=\sum_h\frac1Z\exp\{-E(h,v)\}\\=\sum_h\frac1Z\exp(h^Twv)\cdot\exp(\alpha^T v)\cdot\exp(\beta^T h)\\=\sum_{h_1}\sum_{h_2}\cdots\sum_{h_m}\frac1Z\exp(h^Twv)\cdot\exp(\alpha^T v)\cdot\exp(\beta^T h)\\=\frac1Z\exp(\alpha^T v)\cdot\sum_{h_1}\sum_{h_2}\cdots\sum_{h_m}\exp(h^Twv)\cdot\exp(\beta^T h)\\=\frac1Z\exp(\alpha^T v)\cdot\sum_{h_1}\sum_{h_2}\cdots\sum_{h_m}\exp(\sum^m_{i=1}(h_iw_iv+\beta_i h_i))\\=\frac1Z\exp(\alpha^T v)\cdot\sum_{h_1}\sum_{h_2}\cdots\sum_{h_m}\exp(h_1w_1v+\beta_1 h_1)\cdot\exp(h_2w_2v+\beta_2 h_2)\cdots\exp(h_mw_mv+\beta_mh_m)\\=\frac1Z\exp(\alpha^T v)\cdot\sum_{h_1}\exp(h_1w_1v+\beta_1 h_1)\cdot\sum_{h_2}\exp(h_2w_2v+\beta_2 h_2)\cdots\sum_{h_m}\exp(h_mw_mv+\beta_mh_m)\\=\frac1Z\exp(\alpha^T v)\cdot(1+\exp(w_1v+\beta_1))\cdot(1+\exp(w_2v+\beta_2))\cdots(1+\exp(w_mv+\beta_m))\\=\frac1Z\exp(\alpha^T v)\cdot\exp\{\log(1+\exp(w_1v+\beta_1))\}\cdot\exp\{\log(1+\exp(w_2v+\beta_2))\}\cdots\exp\{\log(1+\exp(w_mv+\beta_m))\}\\=\frac1Z\exp(\alpha^T v+\sum_{i=1}^m\underset{softplus\;function}{\underbrace{\log(1+\exp(w_iv+\beta_i))}})\\=\frac1Z\exp(\alpha^T v+\sum_{i=1}^msoftplus(w_iv+\beta_i)) p(v)=h∑p(h,v)=h∑Z1exp{ −E(h,v)}=h∑Z1exp(hTwv)⋅exp(αTv)⋅exp(βTh)=h1∑h2∑⋯hm∑Z1exp(hTwv)⋅exp(αTv)⋅exp(βTh)=Z1exp(αTv)⋅h1∑h2∑⋯hm∑exp(hTwv)⋅exp(βTh)=Z1exp(αTv)⋅h1∑h2∑⋯hm∑exp(i=1∑m(hiwiv+βihi))=Z1exp(αTv)⋅h1∑h2∑⋯hm∑exp(h1w1v+β1h1)⋅exp(h2w2v+β2h2)⋯exp(hmwmv+βmhm)=Z1exp(αTv)⋅h1∑exp(h1w1v+β1h1)⋅h2∑exp(h2w2v+β2h2)⋯hm∑exp(hmwmv+βmhm)=Z1exp(αTv)⋅(1+exp(w1v+β1))⋅(1+exp(w2v+β2))⋯(1+exp(wmv+βm))=Z1exp(αTv)⋅exp{ log(1+exp(w1v+β1))}⋅exp{ log(1+exp(w2v+β2))}⋯exp{ log(1+exp(wmv+βm))}=Z1exp(αTv+i=1∑msoftplusfunction log(1+exp(wiv+βi)))=Z1exp(αTv+i=1∑msoftplus(wiv+βi))
softplus function: f ( x ) = log ( 1 + e x ) f(x)=\log(1+e^x) f(x)=log(1+ex)
所以,
p ( v ) = 1 Z exp ( α T v + ∑ i = 1 m s o f t p l u s ( w i v + β i ) ) 其 中 , w i 是 w 矩 阵 的 行 向 量 p(v)=\frac1Z\exp(\alpha^T v+\sum_{i=1}^msoftplus(w_iv+\beta_i))\\其中,w_i是w矩阵的行向量 p(v)=Z1exp(αTv+i=1∑msoftplus(wiv+βi))其中,wi是w矩阵的行向量
Learning问题求解可以查看:白板推导系列笔记(二十四)-直面配分函数的第四大点。
Stacking RBM可以查看:白板推导系列笔记(二十七)-深度信念网络的第二大点。
\;
\;
\;
\;
\;
\;
\;
下一章传送门:白板推导系列笔记(二十二)-谱聚类