【LeetCode】5.最长回文子串(中心扩散法,动态规划,超详细图文,java实现)
分析
说明:
- 以下解法中「暴力算法」是基础,「动态规划」必须掌握,「中心扩散」方法要会写;
- 「Manacher 算法」仅用于扩宽视野,绝大多数的算法面试中,面试官都不会要求写这个方法(除非面试者是竞赛选手)。
方法一:暴力匹配 (Brute Force)
- 根据回文子串的定义,枚举所有长度大于等于 22 的子串,依次判断它们是否是回文;
- 在具体实现时,可以只针对大于“当前得到的最长回文子串长度”的子串进行“回文验证”;
- 在记录最长回文子串的时候,可以只记录“当前子串的起始位置”和“子串长度”,不必做截取。这一步我们放在后面的方法中实现。
说明:暴力解法时间复杂度高,但是思路清晰、编写简单。由于编写正确性的可能性很大,可以使用暴力匹配算法检验我们编写的其它算法是否正确。优化的解法在很多时候,是基于“暴力解法”,以空间换时间得到的,因此思考清楚暴力解法,分析其缺点,很多时候能为我们打开思路。
参考代码 1:Java 代码正常运行,C++ 代码超出内存限制,Python 代码超时。
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// s.charAt(i) 每次都会检查数组下标越界,因此先转换成字符数组
char[] charArray = s.toCharArray();
// 枚举所有长度大于 1 的子串 charArray[i..j]
for (int i = 0; i < len - 1; i++) {
for (int j = i + 1; j < len; j++) {
if (j - i + 1 > maxLen && validPalindromic(charArray, i, j)) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
/**
* 验证子串 s[left..right] 是否为回文串
*/
private boolean validPalindromic(char[] charArray, int left, int right) {
while (left < right) {
if (charArray[left] != charArray[right]) {
return false;
}
left++;
right--;
}
return true;
}
}
复杂度分析:
- 时间复杂度: O ( N 3 ) O(N^3) O(N3),这里 N是字符串的长度,枚举字符串的左边界、右边界,然后继续验证子串是否是回文子串,这三种操作都与 N 相关;
- 空间复杂度:O(1),只使用到常数个临时变量,与字符串长度无关。
方法二:动态规划
下面是「动态规划』问题的思考路径,供大家参考。
特别说明:
- 以下「动态规划」的解释只帮助大家了解「动态规划」问题的基本思想;
- 「动态规划」问题可以难到非常难,在学习的时候建议不要钻到特别难的问题中去;
- 掌握经典的动态规划问题的解法,理解状态的定义的由来、会列出状态转移方程;
- 然后再配合适当难度的问题的练习;
- 有时间和感兴趣的话可以做一些不太常见的类型的问题,拓宽视野;
- 「动态规划」讲得比较好的经典书籍是《算法导论》。
提示:右键「在新便签页打开图片」可查看大图。
1、思考状态(重点)
- 状态的定义,先尝试「题目问什么,就把什么设置为状态」;
- 然后思考「状态如何转移」,如果「状态转移方程」不容易得到,尝试修改定义,目的依然是为了方便得到「状态转移方程」。
「状态转移方程」是原始问题的不同规模的子问题的联系。即大问题的最优解如何由小问题的最优解得到。
2、思考状态转移方程(核心、难点)
- 状态转移方程是非常重要的,是动态规划的核心,也是难点;
- 常见的推导技巧是:分类讨论。即:对状态空间进行分类;
- 归纳「状态转移方程」是一个很灵活的事情,通常是具体问题具体分析;
- 除了掌握经典的动态规划问题以外,还需要多做题;
- 如果是针对面试,请自行把握难度。掌握常见问题的动态规划解法,理解动态规划解决问题,是从一个小规模问题出发,逐步得到大问题的解,并记录中间过程;
- 「动态规划」方法依然是「空间换时间」思想的体现,常见的解决问题的过程很像在「填表」。
3、思考初始化
初始化是非常重要的,一步错,步步错。初始化状态一定要设置对,才可能得到正确的结果。
- 角度 1:直接从状态的语义出发;
- 角度 2:如果状态的语义不好思考,就考虑「状态转移方程」的边界需要什么样初始化的条件;
- 角度 3:从「状态转移方程」方程的下标看是否需要多设置一行、一列表示「哨兵」(sentinel),这样可以避免一些特殊情况的讨论。
4、思考输出
有些时候是最后一个状态,有些时候可能会综合之前所有计算过的状态。
5、思考优化空间(也可以叫做表格复用)
- 「优化空间」会使得代码难于理解,且是的「状态」丢失原来的语义,初学的时候可以不一步到位。先把代码写正确是更重要;
- 「优化空间」在有一种情况下是很有必要的,那就是状态空间非常庞大的时候(处理海量数据),此时空间不够用,就必须「优化空间」;
- 非常经典的「优化空间」的典型问题是「0-1 背包」问题和「完全背包」问题。
(下面是这道问题「动态规划」方法的分析)
这道题比较烦人的是判断回文子串。因此需要一种能够快速判断原字符串的所有子串是否是回文子串的方法,于是想到了「动态规划」。
「动态规划」的一个关键的步骤是想清楚「状态如何转移」。事实上,「回文」天然具有「状态转移」性质。
- 一个回文去掉两头以后,剩下的部分依然是回文(这里暂不讨论边界情况);
依然从回文串的定义展开讨论:
- 如果一个字符串的头尾两个字符都不相等,那么这个字符串一定不是回文串;
- 如果一个字符串的头尾两个字符相等,才有必要继续判断下去。
- 如果里面的子串是回文,整体就是回文串;
- 如果里面的子串不是回文串,整体就不是回文串。
即:在头尾字符相等的情况下,里面子串的回文性质据定了整个子串的回文性质,这就是状态转移。因此可以把「状态」定义为原字符串的一个子串是否为回文子串。
第 1 步:定义状态
dp[i][j] 表示子串 s[i..j] 是否为回文子串,这里子串 s[i..j] 定义为左闭右闭区间,可以取到 s[i] 和 s[j]。
第 2 步:思考状态转移方程
在这一步分类讨论(根据头尾字符是否相等),根据上面的分析得到:
dp[i][j] = (s[i] == s[j]) and dp[i + 1][j - 1]
说明:
- 「动态规划」事实上是在填一张二维表格,由于构成子串,因此
i和j的关系是i <= j,因此,只需要填这张表格对角线以上的部分。 - 看到
dp[i + 1][j - 1]就得考虑边界情况。
边界条件是:表达式 [i + 1, j - 1] 不构成区间,即长度严格小于 2,即 j - 1 - (i + 1) + 1 < 2 ,整理得 j - i < 3。
这个结论很显然:j - i < 3 等价于 j - i + 1 < 4,即当子串 s[i..j] 的长度等于 2 或者等于 3 的时候,其实只需要判断一下头尾两个字符是否相等就可以直接下结论了。
- 如果子串
s[i + 1..j - 1]只有 1 个字符,即去掉两头,剩下中间部分只有 11 个字符,显然是回文; - 如果子串
s[i + 1..j - 1]为空串,那么子串s[i, j]一定是回文子串。
因此,在 s[i] == s[j] 成立和 j - i < 3 的前提下,直接可以下结论,dp[i][j] = true,否则才执行状态转移。
第 3 步:考虑初始化
初始化的时候,单个字符一定是回文串,因此把对角线先初始化为 true,即 dp[i][i] = true 。
事实上,初始化的部分都可以省去。因为只有一个字符的时候一定是回文,dp[i][i] 根本不会被其它状态值所参考。
第 4 步:考虑输出
只要一得到 dp[i][j] = true,就记录子串的长度和起始位置,没有必要截取,这是因为截取字符串也要消耗性能,记录此时的回文子串的「起始位置」和「回文长度」即可。
第 5 步:考虑优化空间
因为在填表的过程中,只参考了左下方的数值。事实上可以优化,但是增加了代码编写和理解的难度,丢失可读和可解释性。在这里不优化空间。
注意事项:总是先得到小子串的回文判定,然后大子串才能参考小子串的判断结果,即填表顺序很重要。
大家能够可以自己动手,画一下表格,相信会对「动态规划」作为一种「表格法」有一个更好的理解。
参考代码 2:
public class Solution {
public String longestPalindrome(String s) {
// 特判
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i, j] 是否是回文串
boolean[][] dp = new boolean[len][len];
char[] charArray = s.toCharArray();
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
for (int j = 1; j < len; j++) {
for (int i = 0; i < j; i++) {
if (charArray[i] != charArray[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][j] == true 成立,就表示子串 s[i..j] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
}
复杂度分析:
- 时间复杂度: O ( N 2 ) O(N^{2}) O(N2)。
- 空间复杂度: O ( N 2 ) O(N^{2}) O(N2),二维 dp 问题,一个状态得用二维有序数对表示,因此空间复杂度是 O ( N 2 ) O(N^{2}) O(N2)。
写完代码以后,可以纸上写下代码运行的流程,以字符串 'babad' 为例:
![]()
可以发现:
1、当 i 和 j (图中是 l 和 r) 的差距等于小于 3 的时候,dp 值可以直接判断,不用参考以前的 dp 值;
2、其它情况,每当计算新 dp 值的时候,都一定会参考「左下角」的 dp 值,即 dp[i + 1][j - 1](i + 1 表示在下边,j - 1 表示在左边)。
因此,从上到下写,或者从下到上写,都是可以的。
下面分别展示了错误的填表顺序和正确的填表顺序,以便大家理解动态规划要满足「无后效性」的意思。
说明:表格中的数字表示「填表顺序」,从 1 开始。表格外的箭头和数字也表示「填表顺序」,与表格中的数字含义一致。
参考代码 3:下面这段代码只有内层循环和「参考代码 2」不同,已经标注在注释中。
import java.util.Arrays;
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
boolean[][] dp = new boolean[len][len];
for (int i = 0; i < len; i++) {
Arrays.fill(dp[i], false);
}
// 初始化
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
char[] charArray = s.toCharArray();
int maxLen = 1;
int start = 0;
for (int j = 1; j < len; j++) {
// 只有下面这一行和「参考代码 2」不同,i 正着写、倒过来写都行,因为子串都有参考值
for (int i = j - 1; i >= 0; i--) {
if (charArray[i] == charArray[j]) {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
} else {
dp[i][j] = false;
}
// 只要 dp[i][j] == true 成立,就表示子串 s[i, j] 是回文,此时记录回文长度和起始位置
if (dp[i][j]) {
int curLen = j - i + 1;
if (curLen > maxLen) {
maxLen = curLen;
start = i;
}
}
}
}
return s.substring(start, start + maxLen);
}
}
复杂度分析:(同上)
「状态转移方程」其实可以写得更酷一点:借用 or 的短路功能,如果 j - i < 3 成立,其实后面就不用计算了,状态转移方程可以写成如下:
dp[i][j] = (s[i] == s[j]) and (j - i < 3 or dp[i + 1][j - 1])
以下代码虽然看起来短了一些,但是丢失了可读性,逻辑运算符混用,虽然加上了括号表示优先级,但如果没有前文铺垫,很难读懂是什么意思。不太推荐大家这么写。
参考代码 4:
import java.util.Arrays;
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
boolean[][] dp = new boolean[len][len];
for (int i = 0; i < len; i++) {
Arrays.fill(dp[i], false);
}
// 初始化
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
char[] charArray = s.toCharArray();
int maxLen = 1;
int start = 0;
for (int j = 1; j < len; j++) {
for (int i = 0; i < j; i++) {
dp[i][j] = charArray[i] == charArray[j] && (j - i < 3 || dp[i + 1][j - 1]);
// 只要 dp[i][j] == true 成立,就表示子串 s[i, j] 是回文,此时记录回文长度和起始位置
if (dp[i][j]) {
int curLen = j - i + 1;
if (curLen > maxLen) {
maxLen = curLen;
start = i;
}
}
}
}
return s.substring(start, start + maxLen);
}
}
复杂度分析:(同上)
总结:
- 我们看到,用「动态规划」方法解决问题,有的时候并不是直接面向问题的。
- 「动态规划」依然是「空间换时间」思想的体现,并且本身「动态规划」作为一种打表格法,就是在用「空间」换「时间」。
关于「动态规划」方法执行时间慢的说明:
- 动态规划本质上还是「暴力解法」,因为需要枚举左右边界,有 O ( N 2 ) O(N^2) O(N2)这么多;
- 以下提供的「中心扩散法」枚举了所有可能的回文子串的中心,有 O(2N) 这么多,不在一个级别上。
上面采用了时间复杂度估算的表示, O ( N 2 ) O(N^2) O(N2)表示最高项是 a N 2 aN^2 aN2 的多项式。
从这个问题我们也可以看出,虽然时间复杂度一样,但是实际执行时间有可能是有差距的,并且时间复杂度是一个估算,没有必要计算得很清楚,这是因为真正的运行时间还和很多因素有关:例如所运行机器的环境,测试用例等。
方法三:中心扩散法
暴力法采用双指针两边夹,验证是否是回文子串。
除了枚举字符串的左右边界以外,比较容易想到的是枚举可能出现的回文子串的“中心位置”,从“中心位置”尝试尽可能扩散出去,得到一个回文串。
因此中心扩散法的思路是:遍历每一个索引,以这个索引为中心,利用“回文串”中心对称的特点,往两边扩散,看最多能扩散多远。
枚举“中心位置”时间复杂度为 O(N),从“中心位置”扩散得到“回文子串”的时间复杂度为 O(N),因此时间复杂度可以降到 O ( N 2 ) O(N^2) O(N2)。
在这里要注意一个细节:回文串在长度为奇数和偶数的时候,“回文中心”的形式是不一样的。
- 奇数回文串的“中心”是一个具体的字符,例如:回文串
"aba"的中心是字符"b"; - 偶数回文串的“中心”是位于中间的两个字符的“空隙”,例如:回文串串
"abba"的中心是两个"b"中间的那个“空隙”。
我们看一下一个字符串可能的回文子串的中心在哪里?
![]()
我们可以设计一个方法,兼容以上两种情况:
1、如果传入重合的索引编码,进行中心扩散,此时得到的回文子串的长度是奇数;
2、如果传入相邻的索引编码,进行中心扩散,此时得到的回文子串的长度是偶数。
具体编码细节在以下的代码的注释中体现。
参考代码 5:
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
String res = s.substring(0, 1);
// 中心位置枚举到 len - 2 即可
for (int i = 0; i < len - 1; i++) {
String oddStr = centerSpread(s, i, i);
String evenStr = centerSpread(s, i, i + 1);
String maxLenStr = oddStr.length() > evenStr.length() ? oddStr : evenStr;
if (maxLenStr.length() > maxLen) {
maxLen = maxLenStr.length();
res = maxLenStr;
}
}
return res;
}
private String centerSpread(String s, int left, int right) {
// left = right 的时候,此时回文中心是一个字符,回文串的长度是奇数
// right = left + 1 的时候,此时回文中心是一个空隙,回文串的长度是偶数
int len = s.length();
int i = left;
int j = right;
while (i >= 0 && j < len) {
if (s.charAt(i) == s.charAt(j)) {
i--;
j++;
} else {
break;
}
}
// 这里要小心,跳出 while 循环时,恰好满足 s.charAt(i) != s.charAt(j),因此不能取 i,不能取 j
return s.substring(i + 1, j);
}
}
复杂度分析:
- 时间复杂度: O ( N 2 ) O(N^{2}) O(N2),理由已经叙述。
- 空间复杂度:O(1),只使用到常数个临时变量,与字符串长度无关。
事实上,还有时间复杂度更优的算法,是由计算机科学家 Manacher 发明的,下面介绍这种算法。
方法四:Manacher 算法(不用掌握,面试的时候绝大多数情况下不会要求写这个算法,了解思想即可)
说明:以下题解中有一些细节我当时做的时候,没有仔细推敲,已经有朋友指出有错误,请大家根据自己的理解去思考科学家的做法和思想,我暂时没有时间修改这个部分的内容,大家也可以参考其他朋友的题解,给大家造成不便,我很抱歉。
个人觉得知道 Manacher 算法是基于“中心扩散法”,采用和 kmp 算法类似的思想,依然是“以空间换时间”。
Manacher 算法,被中国程序员戏称为“马拉车”算法。它专门用于解决“最长回文子串”问题,时间复杂度为 O(N)O(N)。
维基百科中对于 Manacher 算法是这样描述的:
[Manacher(1975)] 发现了一种线性时间算法,可以在列出给定字符串中从字符串头部开始的所有回文。并且,Apostolico, Breslauer & Galil (1995) 发现,同样的算法也可以在任意位置查找全部最大回文子串,并且时间复杂度是线性的。因此,他们提供了一种时间复杂度为线性的最长回文子串解法。替代性的线性时间解决 Jeuring (1994), Gusfield (1997)提供的,基于后缀树(suffix trees)。也存在已知的高效并行算法。
Manacher 算法本质上还是中心扩散法,只不过它使用了类似 KMP 算法的技巧,充分挖掘了已经进行回文判定的子串的特点,在遍历的过程中,记录了已经遍历过的子串的信息,也是典型的以空间换时间思想的体现。
下面介绍 Manacher 算法的具体流程。
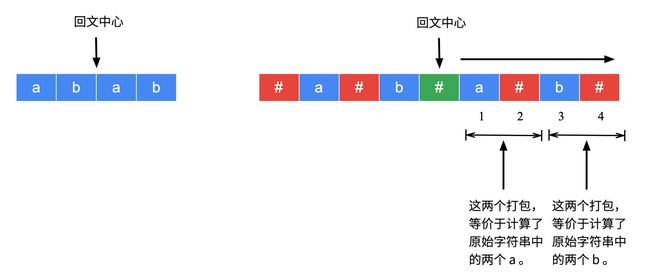
第 1 步:对原始字符串进行预处理(添加分隔符)
首先在字符串的首尾、相邻的字符中插入分隔符,例如 "babad" 添加分隔符 "#" 以后得到 "#b#a#b#a#d#"。
对这一点有如下说明:
1、分隔符是一个字符,种类也只有一个,并且这个字符一定不能是原始字符串中出现过的字符;
2、加入了分隔符以后,使得“间隙”有了具体的位置,方便后续的讨论,并且新字符串中的任意一个回文子串在原始字符串中的一定能找到唯一的一个回文子串与之对应,因此对新字符串的回文子串的研究就能得到原始字符串的回文子串;
3、新字符串的回文子串的长度一定是奇数;
4、新字符串的回文子串一定以分隔符作为两边的边界,因此分隔符起到“哨兵”的作用。
第 2 步:计算辅助数组 p
辅助数组 p 记录了新字符串中以每个字符为中心的回文子串的信息。
手动的计算方法仍然是“中心扩散法”,此时记录以当前字符为中心,向左右两边同时扩散,记录能够扩散的最大步数。
以字符串 "abbabb" 为例,说明如何手动计算得到辅助数组 p ,我们要填的就是下面这张表。
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p |
第 1 行数组 char :原始字符串加上分隔符以后的每个字符。
第 2 行数组 index :这个数组是新字符串的索引数组,它的值是从 00 开始的索引编号。
- 我们首先填
p[0]。
以 char[0] = '#'为中心,同时向左边向右扩散,走 11 步就碰到边界了,因此能扩散的步数为 00,因此 p[0] = 0;
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 0 |
- 下面填写
p[1]。
以 char[1] = 'a' 为中心,同时向左边向右扩散,走 11 步,左右都是 "#",构成回文子串,于是再继续同时向左边向右边扩散,左边就碰到边界了,最多能扩散的步数”为 11,因此 p[1] = 1;
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 0 | 1 |
- 下面填写
p[2]。
以 char[2] = '#'为中心,同时向左边向右扩散,走 11 步,左边是 "a",右边是 "b",不匹配,最多能扩散的步数为 00,因此 p[2] = 0;
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 0 | 1 | 0 |
- 下面填写
p[3]。
以 char[3] = 'b' 为中心,同时向左边向右扩散,走 11 步,左右两边都是 “#”,构成回文子串,继续同时向左边向右扩散,左边是 "a",右边是 "b",不匹配,最多能扩散的步数为 11 ,因此 p[3] = 1;
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 0 | 1 | 0 | 1 |
- 下面填写
p[4]。
以 char[4] = '#' 为中心,同时向左边向右扩散,最多可以走 44 步,左边到达左边界,因此 p[4] = 4。
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 0 | 1 | 0 | 1 | 4 |
- 继续填完 p 数组剩下的部分。
分析到这里,后面的数字不难填出,最后写成如下表格:
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 0 | 1 | 0 | 1 | 4 | 1 | 0 | 5 | 0 | 1 | 2 | 1 | 0 |
说明:有些资料将辅助数组 p 定义为回文半径数组,即 p[i] 记录了以新字符串第 i 个字符为中心的回文字符串的半径(包括第 i 个字符),与我们这里定义的辅助数组 p 有一个字符的偏差,本质上是一样的。
下面是辅助数组 p 的结论:辅助数组 p 的最大值是 55,对应了原字符串 "abbabb" 的 “最长回文子串” :"bbabb"。这个结论具有一般性,即:
辅助数组
p的最大值就是“最长回文子串”的长度。
因此,我们可以在计算辅助数组 p 的过程中记录这个最大值,并且记录最长回文子串。
简单说明一下这是为什么:
- 如果新回文子串的中心是一个字符,那么原始回文子串的中心也是一个字符,在新回文子串中,向两边扩散的特点是:“先分隔符,后字符”,同样扩散的步数因为有分隔符
#的作用,在新字符串中每扩散两步,虽然实际上只扫到一个有效字符,但是相当于在原始字符串中相当于计算了两个字符。因为最后一定以分隔符结尾,还要计算一个,正好这个就可以把原始回文子串的中心算进去;
- 如果新回文子串的中心是
#,那么原始回文子串的中心就是一个“空隙”。在新回文子串中,向两边扩散的特点是:“先字符,后分隔符”,扩散的步数因为有分隔符#的作用,在新字符串中每扩散两步,虽然实际上只扫到一个有效字符,但是相当于在原始字符串中相当于计算了两个字符。
因此,“辅助数组 p 的最大值就是“最长回文子串”的长度”这个结论是成立的,可以看下面的图理解上面说的 22 点。
写到这里,其实已经能写出一版代码,把这一版代码提交到 LeetCode 是可以通过的,这同样也可以验证我们上面的结论是正确的。
参考代码 6:
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
String str = addBoundaries(s, '#');
int sLen = 2 * len + 1;
int maxLen = 1;
int start = 0;
for (int i = 0; i < sLen; i++) {
int curLen = centerSpread(str, i);
if (curLen > maxLen) {
maxLen = curLen;
start = (i - maxLen) / 2;
}
}
return s.substring(start, start + maxLen);
}
private int centerSpread(String s, int center) {
int len = s.length();
int i = center - 1;
int j = center + 1;
int step = 0;
while (i >= 0 && j < len && s.charAt(i) == s.charAt(j)) {
i--;
j++;
step++;
}
return step;
}
/**
* 创建预处理字符串
*
* @param s 原始字符串
* @param divide 分隔字符
* @return 使用分隔字符处理以后得到的字符串
*/
private String addBoundaries(String s, char divide) {
int len = s.length();
if (len == 0) {
return "";
}
if (s.indexOf(divide) != -1) {
throw new IllegalArgumentException("参数错误,您传递的分割字符,在输入字符串中存在!");
}
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < len; i++) {
stringBuilder.append(divide);
stringBuilder.append(s.charAt(i));
}
stringBuilder.append(divide);
return stringBuilder.toString();
}
}
复杂度分析:
- 时间复杂度: O ( N 2 ) O(N^2) O(N2),这里 NN 是原始字符串的长度。新字符串的长度是$ 2 \times N+ 1 , 不 计 系 数 与 常 数 项 , 因 此 时 间 复 杂 度 仍 为 ,不计系数与常数项,因此时间复杂度仍为 ,不计系数与常数项,因此时间复杂度仍为 O(N^2)$。
- 空间复杂度:O(N)。
科学家的工作:充分利用新字符串的回文性质,计算辅助数组
p。
上面的代码不太智能的地方是,对新字符串每一个位置进行中心扩散,会导致原始字符串的每一个字符被访问多次,一个比较极端的情况就是:#a#a#a#a#a#a#a#a#。事实上,计算机科学家 Manacher 就改进了这种算法,使得在填写新的辅助数组 p 的值的时候,能够参考已经填写过的辅助数组 p 的值,使得新字符串每个字符只访问了一次,整体时间复杂度由 O ( N 2 ) O(N^2) O(N2) 改进到 O(N)。
具体做法是:在遍历的过程中,除了循环变量 i 以外,我们还需要记录两个变量,它们是 maxRight 和 center ,它们分别的含义如下:
maxRight:记录当前向右扩展的最远边界,即从开始到现在使用“中心扩散法”能得到的回文子串,它能延伸到的最右端的位置 。对于maxRight我们说明 3 点:
- “向右最远”是在计算辅助数组
p的过程中,向右边扩散能走的索引最大的位置,注意:得到一个maxRight所对应的回文子串,并不一定是当前得到的“最长回文子串”,很可能的一种情况是,某个回文子串可能比较短,但是它正好在整个字符串比较靠后的位置; maxRight的下一个位置可能是被程序看到的,停止的原因有 2 点:(1)左边界不能扩散,导致右边界受限制也不能扩散,maxRight的下一个位置看不到;(2)正是因为看到了maxRight的下一个位置,导致maxRight不能继续扩散。- 为什么
maxRight很重要?因为扫描是从左向右进行的,maxRight能够提供的信息最多,它是一个重要的分类讨论的标准,因此我们需要一个变量记录它。
center:center是与maxRight相关的一个变量,它是上述maxRight的回文中心的索引值。对于center的说明如下:
center的形式化定义:
center = argmax {x + p[x] ; | ; 0 \leq x< i }cente**r=argma**x{ x+p[x]∣0≤x<i}
说明:x + p[x] 的最大值就是我们定义的 maxRight,i 是循环变量,0<= x< i表示是在 i 之前的所有索引里得到的最大值 maxRight,它对应的回文中心索引就是上述式子。
maxRight与center是一一对应的关系,即一个center的值唯一对应了一个maxRight的值;因此maxRight与center必须要同时更新。
下面的讨论就根据循环变量 i 与 maxRight 的关系展开讨论:
情况 1:当 i >= maxRight 的时候,这就是一开始,以及刚刚把一个回文子串扫描完的情况,此时只能够根据“中心扩散法”一个一个扫描,逐渐扩大 maxRight;
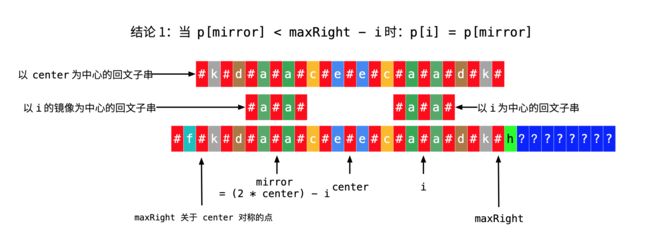
情况 2:当 i < maxRight 的时候,根据新字符的回文子串的性质,循环变量关于 center 对称的那个索引(记为 mirror)的 p 值就很重要。
我们先看 mirror 的值是多少,因为 center 是中心,i 和 mirror 关于 center 中心对称,因此 (mirror + i) / 2 = center ,所以 mirror = 2 * center - i。
根据 p[mirror] 的数值从小到大,具体可以分为如下 3 种情况:
情况 2(1):p[mirror] 的数值比较小,不超过 maxRight - i。
说明:maxRight - i 的值,就是从 i 关于 center 的镜像点开始向左走(不包括它自己),到 maxRight 关于 center 的镜像点的步数
从图上可以看出,由于“以 center 为中心的回文子串”的对称性,导致了“以 i 为中心的回文子串”与“以 center 为中心的回文子串”也具有对称性,“以 i 为中心的回文子串”与“以 center 为中心的回文子串”不能再扩散了,此时,直接把数值抄过来即可,即 p[i] = p[mirror]。
情况 2(2):p[mirror] 的数值恰好等于 maxRight - i。
说明:仍然是依据“以 center 为中心的回文子串”的对称性,导致了“以 i 为中心的回文子串”与“以 center 为中心的回文子串”也具有对称性。
- 因为靠左边的
f与靠右边的g的原因,导致“以center为中心的回文子串”不能继续扩散; - 但是“以
i为中心的回文子串” 还可以继续扩散。
因此,可以先把 p[mirror] 的值抄过来,然后继续“中心扩散法”,继续增加 maxRight。
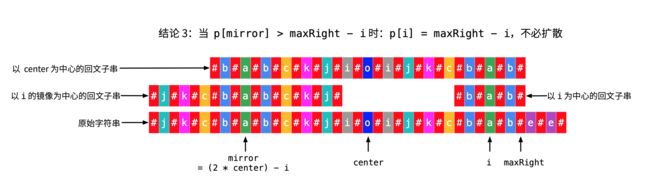
情况 2(3):p[mirror] 的数值大于 maxRight - i。
说明:仍然是依据“以 center 为中心的回文子串”的对称性,导致了“以 i 为中心的回文子串”与“以 center 为中心的回文子串”也具有对称性。
下面证明,p[i] = maxRight - i ,证明的方法还是利用三个回文子串的对称性。
① 由于“以 center 为中心的回文子串”的对称性, 黄色箭头对应的字符 c 和 e 一定不相等;
② 由于“以 mirror 为中心的回文子串”的对称性, 绿色箭头对应的字符 c 和 c 一定相等;
③ 又由于“以 center 为中心的回文子串”的对称性, 蓝色箭头对应的字符 c 和 c 一定相等;
推出“以 i 为中心的回文子串”的对称性, 红色箭头对应的字符 c 和 e 一定不相等。
因此,p[i] = maxRight - i,不可能再大。上面是因为我画的图,可能看的朋友会觉得理所当然。事实上,可以使用反证法证明:
如果“以 i 为中心的回文子串” 再向两边扩散的两个字符 c 和 e 相等,就能够推出黄色、绿色、蓝色、红色箭头所指向的 8 个变量的值都相等,此时“以 center 为中心的回文子串” 就可以再同时向左边和右边扩散 11 格,与 maxRight 的最大性矛盾。
综合以上 3 种情况,当 i < maxRight 的时候,p[i] 可以参考 p[mirror] 的信息,以 maxRight - i 作为参考标准,p[i] 的值应该是保守的,即二者之中较小的那个值:
p[i] = min(maxRight - i, p[mirror]);
参考代码 7:
public class Solution {
public String longestPalindrome(String s) {
// 特判
int len = s.length();
if (len < 2) {
return s;
}
// 得到预处理字符串
String str = addBoundaries(s, '#');
// 新字符串的长度
int sLen = 2 * len + 1;
// 数组 p 记录了扫描过的回文子串的信息
int[] p = new int[sLen];
// 双指针,它们是一一对应的,须同时更新
int maxRight = 0;
int center = 0;
// 当前遍历的中心最大扩散步数,其值等于原始字符串的最长回文子串的长度
int maxLen = 1;
// 原始字符串的最长回文子串的起始位置,与 maxLen 必须同时更新
int start = 0;
for (int i = 0; i < sLen; i++) {
if (i < maxRight) {
int mirror = 2 * center - i;
// 这一行代码是 Manacher 算法的关键所在,要结合图形来理解
p[i] = Math.min(maxRight - i, p[mirror]);
}
// 下一次尝试扩散的左右起点,能扩散的步数直接加到 p[i] 中
int left = i - (1 + p[i]);
int right = i + (1 + p[i]);
// left >= 0 && right < sLen 保证不越界
// str.charAt(left) == str.charAt(right) 表示可以扩散 1 次
while (left >= 0 && right < sLen && str.charAt(left) == str.charAt(right)) {
p[i]++;
left--;
right++;
}
// 根据 maxRight 的定义,它是遍历过的 i 的 i + p[i] 的最大者
// 如果 maxRight 的值越大,进入上面 i < maxRight 的判断的可能性就越大,这样就可以重复利用之前判断过的回文信息了
if (i + p[i] > maxRight) {
// maxRight 和 center 需要同时更新
maxRight = i + p[i];
center = i;
}
if (p[i] > maxLen) {
// 记录最长回文子串的长度和相应它在原始字符串中的起点
maxLen = p[i];
start = (i - maxLen) / 2;
}
}
return s.substring(start, start + maxLen);
}
/**
* 创建预处理字符串
*
* @param s 原始字符串
* @param divide 分隔字符
* @return 使用分隔字符处理以后得到的字符串
*/
private String addBoundaries(String s, char divide) {
int len = s.length();
if (len == 0) {
return "";
}
if (s.indexOf(divide) != -1) {
throw new IllegalArgumentException("参数错误,您传递的分割字符,在输入字符串中存在!");
}
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < len; i++) {
stringBuilder.append(divide);
stringBuilder.append(s.charAt(i));
}
stringBuilder.append(divide);
return stringBuilder.toString();
}
}
复杂度分析:
- 时间复杂度:O(N),Manacher 算法只有在遇到还未匹配的位置时才进行匹配,已经匹配过的位置不再匹配,因此对于字符串
S的每一个位置,都只进行一次匹配,算法的复杂度为 O(N)O(N)。 - 空间复杂度:O(N)。