JAVA-高频面试题汇总:二叉树(一)

前言

为了让小伙伴们更好地刷题,我将所有leetcode常考题按照知识点进行了归纳.
已完成:
JAVA-高频面试题汇总:动态规划
JAVA-高频面试题汇总:二叉树(二)

接下来我对树这一知识点进行归纳总结,树的内容总结了二十多道,将分为几篇文章讲解,归纳基于JAVA语言,是我一边复习一边整理的,如有疑惑欢迎交流!
小编微信: Apollo___quan

JAVA-高频面试题汇总:树(一)

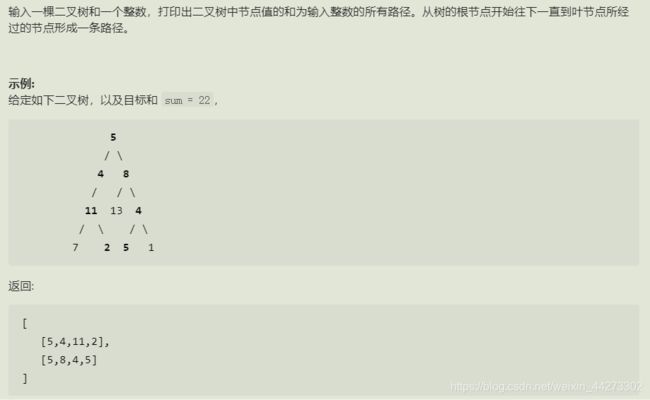
1.二叉树中和为某一值的路径

思路

1.创建path记录路径，用tar记录路径和（tar = tar - root.val）

2.前序遍历，添加当前节点到path，当tar == 0 且无左右子树时将path加到res

3.遍历左子树与右子树，最后一步删除当前节点表示前两步结束后进行回溯

注意的点：

1.ArrayList与LinkedList的remove方法

2.res.add(new ArrayList(path))时传入的应是新的对象而不能时path对象，否则后续path发生变化会影响结果

class Solution {
     
        List<List<Integer>> res = new ArrayList<>(); //List是接口 需要ArrayList或LinkedList实现
        List<Integer> path = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
     
        recur(root, sum);
        return res;
    }
    void recur(TreeNode root, int tar){
     
        if(root==null) return;
        path.add(root.val);
        tar = tar - root.val; //值传递,若回溯不改变上一层的tar值,与path相区别
        if(tar == 0 && root.left ==null && root.right ==null){
     
            res.add(new ArrayList(path));//如果直接传入path,传的是path对象,后续对path的改动都会有影响
        }
        recur(root.left, tar);
        recur(root.right, tar);
        path.remove(path.size()-1); //注意path是全局变量,如果回溯需要删除该节点
    }
}

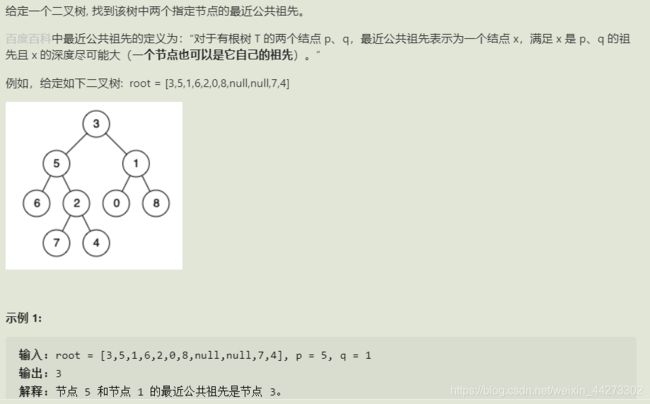
2.二叉树的最近公共祖先

思路

1.递归，可能出现的情况为 ①目标点在root异侧 ②root点为其中一点 ③两侧都没有目标点

2.设置Left与Right遍历左右子树，根据Left与Right讨论上面三种情况，先假设Left与Right的递归合理，否则容易绕晕

class Solution {
     
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
     
        if(root == null || root == p || root == q) return root; //为空树或节点为其中一点,直接返回
        TreeNode Left = lowestCommonAncestor(root.left, p, q);
        TreeNode Right = lowestCommonAncestor(root.right, p, q);
        if(Left == null && Right == null) return null; //左右都无目标点,返回null
        else if(Left == null) return Right; //左子树没有,都在右子树,返回右子树遍历结果
        else if(Right == null) return Left; //右子树没有,都在左子树,返回左子树遍历结果
        else return root; //左右都不为null,说明在两边,该点即为最近公共点
    }
}

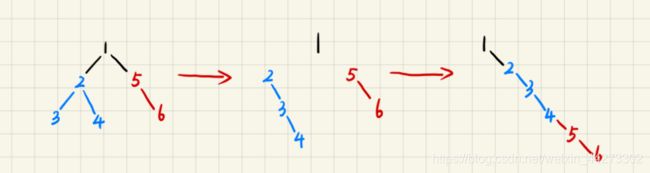
3.二叉树展开为链表

思路

推荐leetcode大佬的解答，思路很清晰

其实是分为三步：

1.首先将根节点的左子树变成链表

2.其次将根节点的右子树变成链表

3.最后将变成链表的右子树放在变成链表的左子树的最右边

这就是一个递归的过程，递归的一个非常重要的点就是：

不去管函数的内部细节是如何处理的，我们只看其函数作用以及输入与输出。

对于函数flatten来说：

1.函数作用：将一个二叉树，原地将它展开为链表
2.输入：树的根节点
3.输出：无

class Solution {
     
    public void flatten(TreeNode root) {
     
        if(root == null){
     
            return ;
        }
        //将根节点的左子树变成链表
        flatten(root.left);
        //将根节点的右子树变成链表
        flatten(root.right);
        TreeNode temp = root.right;
        //把树的右边换成左边的链表
        root.right = root.left;
        //记得要将左边置空
        root.left = null;
        //找到树的最右边的节点
        while(root.right != null) root = root.right;
        //把右边的链表接到刚才树的最右边的节点
        root.right = temp;
    }
}

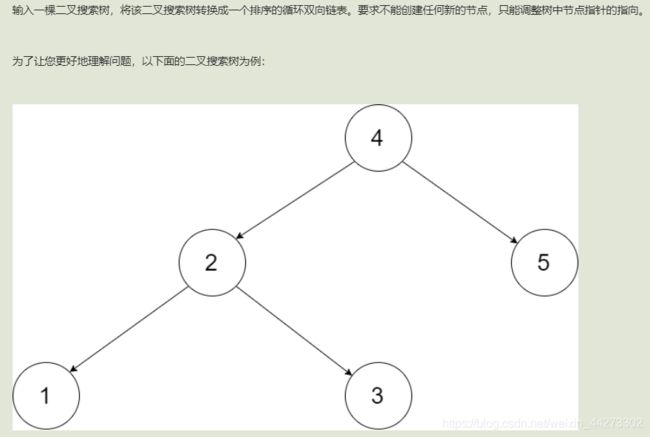
4.二叉搜索树与双向链表

这题与第三题乍一看很像，其实差别很大

思路

1.中序遍历，一边利用pre指针不断记录节点关系

2.注意最后头尾节点的连接，因为是循环双向链表

class Solution {
     
    Node pre = null; 
    Node head; //head为了记录头节点
    public Node treeToDoublyList(Node root) {
     
        if(root == null) return pre;
        dfs(root);
        head.left = pre;
        pre.right = head;
        return head;    
    }
    public void dfs(Node node){
     
        if(node == null) return;
        dfs(node.left);
        if(pre != null) pre.right = node; 
        else head = node;  //head记录头节点
        node.left = pre; //如果是头节点则node = head,最终head.left都要覆盖为pre,所以这一步没影响
        pre = node; //pre指针后移到node
        dfs(node.right);
    }
}

5.二叉树的右视图

思路

其实就是层序遍历只记录每层最后一点

class Solution {
     
    public List<Integer> rightSideView(TreeNode root) {
     
        List<Integer> list = new LinkedList<>();
        Queue<TreeNode> queue=new LinkedList<>();
        if(root == null) return list;
        queue.add(root);
        while(!queue.isEmpty()){
     
            int count = 0;
            int size = queue.size(); //记录长度
            for(int i = 0; i < size; i++){
     
                TreeNode node = queue.poll();
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
                count++;
                if(count == size ){
       //只添加最后一个数据,与层序遍历区别
                    list.add(node.val);
                }
            }
        }
        return list;
    }
}

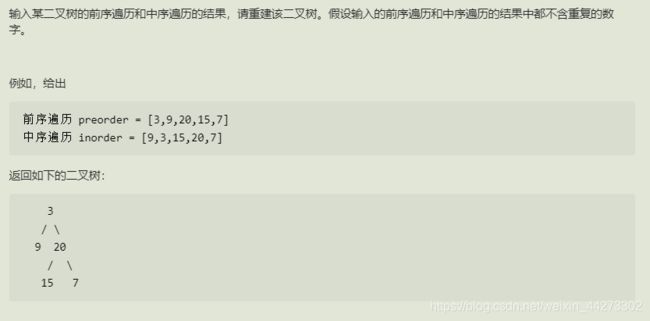
6.重建二叉树

思路

1.利用前序遍历与中序遍历的特性将树分为左子树与右子树

2.化为子问题进行递归，每一代求解root.left与root.right，并返回root

public class Solution {
     
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
     
        if(pre.length==0) return null;
        TreeNode root =new TreeNode(0);
        root.val=pre[0];  //前序遍历的第一个节点即根节点,后面跟着左子树,然后右子树
        int index=0;
        for(int i=0;i<in.length;i++){
      
            if(in[i]==root.val) {
       //中序遍历中找根节点,右边的为右子树,左边的为左子树
                index=i;
                break;
            }
        }
        //将左子树看成一棵二叉树调用该方法，可以得到左子树根结点，即上面根结点的左子结点
        root.left=reConstructBinaryTree(Arrays.copyOfRange(pre,1,index+1),Arrays.copyOfRange(in,0,index));
       //将右子树看成一棵二叉树调用该方法，可以得到右子树根结点，即上面根结点的右子结点
        root.right=reConstructBinaryTree(Arrays.copyOfRange(pre,index+1,pre.length),Arrays.copyOfRange(in,index+1,in.length));
        return root;
    }
}

第二部分已完成
JAVA-高频面试题汇总:二叉树(二)