哈夫曼编码的C#实现和简介

huffman中文叫做哈弗曼，霍夫曼。网上清一色全是C++,C的实现,C#的应该比较少。所以成了写这篇文章的动机。

 

首先哈弗曼算法是一个压缩算法，但只是进行了替换字符的操作，没有合并字符记录位置。很多算法基于哈弗曼又进一步的进行合并等操作。并且哈弗曼编码不仅可以用于压缩，还可以拿他进行简单的加密。

 

实现代码在另一个随笔里：

http://www.cnblogs.com/HONT/archive/2013/06/05/3118679.html

 

相关阅读：

基于哈弗曼的改进，可自定义字典：

http://www.cnblogs.com/HONT/archive/2013/06/05/3118686.html

哈弗曼编码维基百科：

http://zh.wikipedia.org/wiki/%E5%93%88%E5%A4%AB%E6%9B%BC%E7%BC%96%E7%A0%81

 

 

 

 

注:我这里用char字符代替了二进制数据.

===============================================================

 

首先举一个演示例子:

[曼, 0]
[哈, 10]
[夫, 11]
--------------------编码与解析
编码: 101100000
解析: 哈夫曼曼曼曼曼

我输入了"哈夫曼曼曼曼曼"几个字符，它转换成了0101的哈夫曼编码。

这里可以看见重复的字不会重复编码。并且从左往右解析，不会弄混。

当时刚看的时候觉得很神奇，为啥就不会弄混，后来发现是用了树结构达到这个效果。具体下面再说

 

-----------------------------------------------------------------------------------------

来看看哈弗曼算法的流程：

 

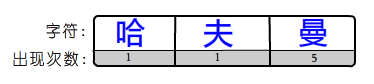
Step1:

首先按照字符的出现次数(权值)排序.放入数组。还以上面的例子为参照

"哈夫曼曼曼曼曼"

这组字符，曼出现的次数最多.

 

 

 

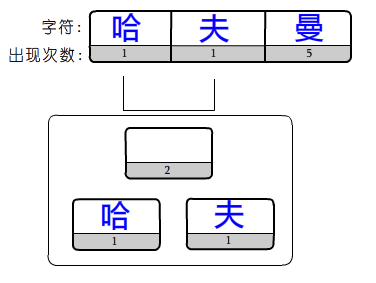
Step2:

创建一个树枝节点，然后把出现次数最少的2个树合并到他的左右树杈(左子树右子树)里。

并且把两个数出现次数相加，变成合并后的权值，合并后的元素是没有名称的，只有权值。

然后把原数组中两个值替换成新创建的树枝节点。

这是霍夫曼最优二叉树的核心，从底向上构建树。而正常是从上向下构建树。

 

 

 

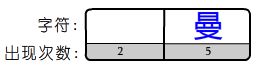
PS:可以看见3个元素的数组，合并后变成了2个元素

 

 

 

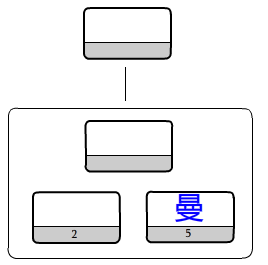
Step3:

再把出现次数最小的两个数合并。直到变成一个元素为止。

至此，哈弗曼最优二叉树构建完成

 

 

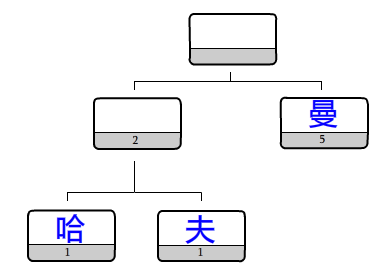
PS:完成后的树，是这个模样

 

 

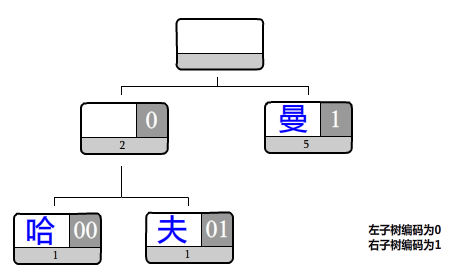
Step4:

按照左子树编码为0，右子树编码为1的规则。对每个节点编码。

因为字符只会出现在叶子节点上，所以不会出现前缀字符的情况。

就是一堆101010101的数据，不会搞混，从左往右解码，必然能正确解析

 

----------------------------------------------------------------------------------

之后只要在对原字符进行统一编码就可以了。

还可以配合LZ77算法等，进一步压缩数据。