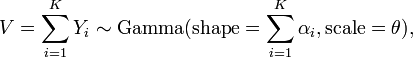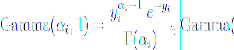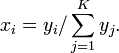Dirichlet分布及其属性
Dirichlet分布
在概率统计中,Dirichlet分布通常表示为![]() ,是一个以正实数
,是一个以正实数![]() 的向量为参数的连续多变量概率分布族。这是Beta分布的多元推广。在贝叶斯统计中,狄氏分布很多情况下可作为先验分布,其实Dirichlet分布是类别分布和多项分布的共轭先验。
的向量为参数的连续多变量概率分布族。这是Beta分布的多元推广。在贝叶斯统计中,狄氏分布很多情况下可作为先验分布,其实Dirichlet分布是类别分布和多项分布的共轭先验。
狄利克雷分布向无限维度的推广便是狄利克雷过程。
Categorical分布
分类分布(有时也被不确切地称为“离散分布”或“多项分布”)从K个概率中的一个来描述事件的发生概率。参数值必须在0、1之间,它们的和为1。分类分布是伯努利分布向多类随机变量的推广。
在分布的表达式中,令采样空间是有限的整数序列。作为标签,这些整数的值并不是重要的,他们可以是{0,1,…,K-1}或{1,2,…,K}或者其他任意值。为了方便,这里我们使用{1,2,…,K}。
概率密度函数为:
另外一种更复杂但利于数学运算的表达式:
严格意义上,分类分布可以看做是多项式分布的一种特殊形式(n=1)。
Dirichlet分布是分类分布和多项分布的共轭先验,这意味着我们可以给分类分布的未知参数![]() 一个服从Dirichlet分布的先验分布。然后,这个参数的后验分布(结合观测数据知识后)也是个Dirichlet分布。这样我们便可以根据每次新的观测值不断的更新参数的分布模型。形式上,解释如下:
一个服从Dirichlet分布的先验分布。然后,这个参数的后验分布(结合观测数据知识后)也是个Dirichlet分布。这样我们便可以根据每次新的观测值不断的更新参数的分布模型。形式上,解释如下:
在给定分类分布的N个抽样集时,可以利用这种关系来估计它的参数![]() 。此时:
。此时:
技术上,某些应用也可以采用:
边缘似然:上述模型中,观测值的边缘似然是Dirichlet-multinomial分布
边缘似然分布在分层贝叶斯模型中扮演着重要的角色,当使用Gibbs抽样或变分贝叶斯来做推断时,Dirichlet先验分布经常需要边缘化。
结论:后验预测概率是后验分布的期望值。
新来数据会以较大的概率分配到以前出现次数较多的类中,这种情况可视作“偏好依附”模型。它与很多现实世界的过程相符,在模型下,起初少量数据点的选择对以后数据的分配将产生巨大的影响。
后验条件分布:在Gibbs抽样中,我们需要在多变量贝叶斯网络组成的条件分布(每一个变量都依赖于其他值)中进行抽样。
抽样过程:
// do multinomial sampling via cumulative method for (int k = 0; k < K; k++) { p[k] = (nw[w][k] + beta) / (nwsum[k] + Vbeta) * (nd[m][k] + alpha) / (ndsum[m] + Kalpha); //1:得到属于每一类的概率 }//这就是ToTGibbs中的公式和text-est文件 // cumulate multinomial parameters for (int k = 1; k < K; k++) { p[k] += p[k - 1]; } //2:得到累计概率分布 // scaled sample because of unnormalized p[] double u = ((double)random() / RAND_MAX) * p[K - 1]; //3:采样均匀分布的值 for (topic = 0; topic < K; topic++) { if (p[topic] > u) { break; } } //4:返回类别
Multinomial分布
在概率理论中,Multinomial分布是二项式分布的推广。Multinomial分布给出了多类问题中,任意类别数组合的概率。
二项分布是n次伯努利分布中,两类组合发生次数的概率分布。
注意:在自然语言处理领域,categorical和multinomial分布是混为一谈的,当提到multinomial分布时实质意味着是categorical分布;当然,categorical也可以视为multinomial的特殊情况。
概率密度函数:假设袋子的球分为k类,我们做n次有放回抽样。来自同一类的球是完全一样的。我们用![]() 表示第i(i=1,…,k)类的球的次数。
表示第i(i=1,…,k)类的球的次数。![]() 表示属于第i类的概率。
表示属于第i类的概率。
属性:在n次实验中,类i的数学期望
协方差矩阵:每一个对角线元素实质是二项分布,因此
非对角线元素
所有的协方差都是负值,因为对于固定的数值n,多类中一类的增加势必导致另类的减少。
返回Dirichlet分布,其概率密度表达式:
其中,![]() 且
且![]() 。上式中
。上式中![]() 表示概率密度公式是个
表示概率密度公式是个![]() 的欧式空间,在不满足条件的空间里密度为0.
的欧式空间,在不满足条件的空间里密度为0.
多项beta函数可以用gama函数表示:
特殊情况:一种比价常见的形式是对称Dirichlet分布0,这里向量![]() 的所有元素取相同值。因为我们通常没有任何先验的知识来确定某个分量要优于其他分量,所以当使用Dirichlet先验时常使用其对称形式。此时的标量
的所有元素取相同值。因为我们通常没有任何先验的知识来确定某个分量要优于其他分量,所以当使用Dirichlet先验时常使用其对称形式。此时的标量![]() 称为concentration parameter(浓度参数)。有:
称为concentration parameter(浓度参数)。有:
当![]() 时,上式与
时,上式与![]() 值无关等价于均匀分布。当
值无关等价于均匀分布。当![]() 时,分布越趋于平稳,在一次抽样中的所有值都趋于相同;当
时,分布越趋于平稳,在一次抽样中的所有值都趋于相同;当![]() 时,分布越趋于尖锐,在一次抽样中,大多数数值趋近于0,只有很少分量具有较大值。
时,分布越趋于尖锐,在一次抽样中,大多数数值趋近于0,只有很少分量具有较大值。
更一般的情况,参数向量有时写成![]() 的形式,其中
的形式,其中![]() 为标量浓度参数,
为标量浓度参数,![]() 是基测量(
是基测量(![]() 的和为1)。主题模型的文献中经常使用这种构造。
的和为1)。主题模型的文献中经常使用这种构造。
属性:假设
由定义得:
边缘分布:Dirichlet分布的边缘分布是beta分布
聚合性质:如果
这个性质可以用来推导出上面提到的边缘分布。
相关分布:
2.
3.那么:
虽然![]() 之间并不是相互独立的,但他们可以通过K个独立的gamma分布得到,详见 Devroye, Luc (1986). Non-Uniform Random Variate Generation. Springer-Verlag. p. 594. (Chapter 11.)。
之间并不是相互独立的,但他们可以通过K个独立的gamma分布得到,详见 Devroye, Luc (1986). Non-Uniform Random Variate Generation. Springer-Verlag. p. 594. (Chapter 11.)。
Gamma分布
使用Gamma分布,我们可以很容易地得到K维![]() Dirichlet分布的抽样
Dirichlet分布的抽样![]() 。首先,从Gamma分布得到K个独立的随机抽样
。首先,从Gamma分布得到K个独立的随机抽样![]() 。
。
然后得:
![clip_image018[7] clip_image018[7]](http://img.e-com-net.com/image/product/08a5fe6f0eba49d0861873c86fbbe958.png)
![clip_image020[7] clip_image020[7]](http://img.e-com-net.com/image/product/6c4147d309a34cb08213a65e4b4c4ca3.png)
![clip_image029[7] clip_image029[7]](http://img.e-com-net.com/image/product/fbb897395a9d49e0b7be0193d5b7ce68.png)
![clip_image031[7] clip_image031[7]](http://img.e-com-net.com/image/product/df19ca68df7b4a8e8359210a7d0d4684.png)
![clip_image037[7] clip_image037[7]](http://img.e-com-net.com/image/product/d9edd2a78954442fb6a25cde455b6376.png)
![clip_image039[7] clip_image039[7]](http://img.e-com-net.com/image/product/c9ca1691a1264da185f6fcab61a61c26.png)
![clip_image045[10] clip_image045[10]](http://img.e-com-net.com/image/product/05020f86bef74dadb5d21592e99aae6c.png)
![clip_image006[9] clip_image006[9]](http://img.e-com-net.com/image/product/fbdd26fdcfb14bc3a62dbb8eca3fd863.png)
![clip_image010[9] clip_image010[9]](http://img.e-com-net.com/image/product/e4a3718aedce42b2b97a37b8cf65c110.png)
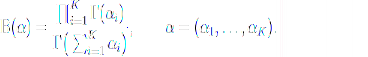
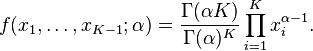
![clip_image047[9] clip_image047[9]](http://img.e-com-net.com/image/product/7ab57cdd30054470ae126e82c5e23174.png)